Free Parametrization of L2-bounded State Space Models

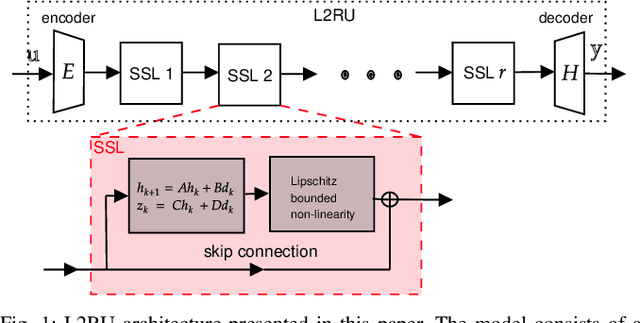
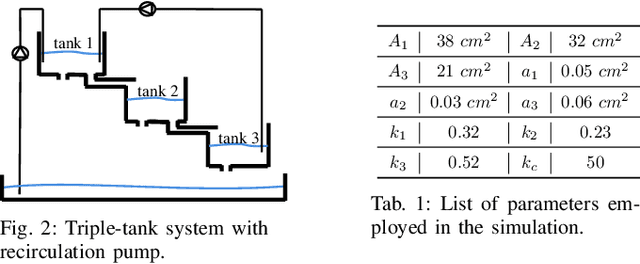
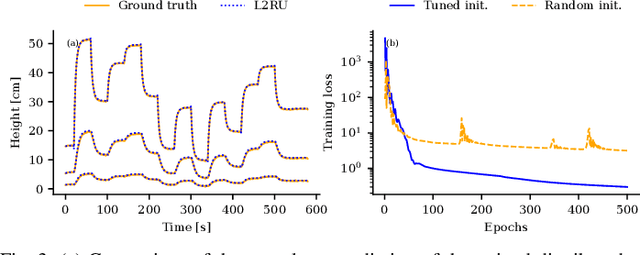
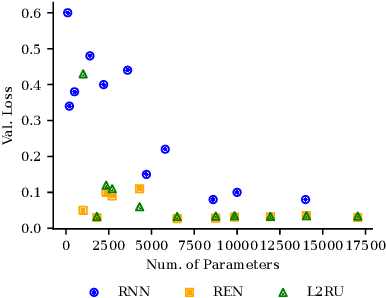
Structured state-space models (SSMs) have emerged as a powerful architecture in machine learning and control, featuring stacked layers where each consists of a linear time-invariant (LTI) discrete-time system followed by a nonlinearity. While SSMs offer computational efficiency and excel in long-sequence predictions, their widespread adoption in applications like system identification and optimal control is hindered by the challenge of ensuring their stability and robustness properties. We introduce L2RU, a novel parametrization of SSMs that guarantees input-output stability and robustness by enforcing a prescribed L-bound for all parameter values. This design eliminates the need for complex constraints, allowing unconstrained optimization over L2RUs by using standard methods such as gradient descent. Leveraging tools from system theory and convex optimization, we derive a non-conservative parametrization of square discrete-time LTI systems with a specified L2-bound, forming the foundation of the L2RU architecture. Additionally, we enhance its performance with a bespoke initialization strategy optimized for long input sequences. Through a system identification task, we validate L2RU's superior performance, showcasing its potential in learning and control applications.

Contractive Dynamical Imitation Policies for Efficient Out-of-Sample Recovery

Imitation learning is a data-driven approach to learning policies from expert behavior, but it is prone to unreliable outcomes in out-of-sample (OOS) regions. While previous research relying on stable dynamical systems guarantees convergence to a desired state, it often overlooks transient behavior. We propose a framework for learning policies using modeled by contractive dynamical systems, ensuring that all policy rollouts converge regardless of perturbations, and in turn, enable efficient OOS recovery. By leveraging recurrent equilibrium networks and coupling layers, the policy structure guarantees contractivity for any parameter choice, which facilitates unconstrained optimization. Furthermore, we provide theoretical upper bounds for worst-case and expected loss terms, rigorously establishing the reliability of our method in deployment. Empirically, we demonstrate substantial OOS performance improvements in robotics manipulation and navigation tasks in simulation.

Neural Port-Hamiltonian Models for Nonlinear Distributed Control: An Unconstrained Parametrization Approach

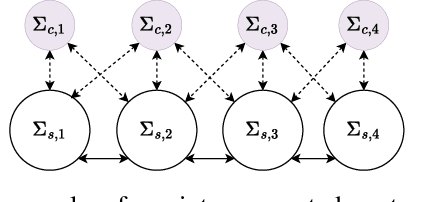
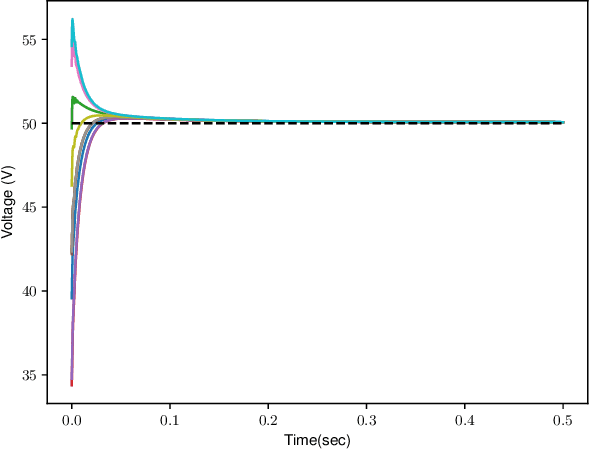
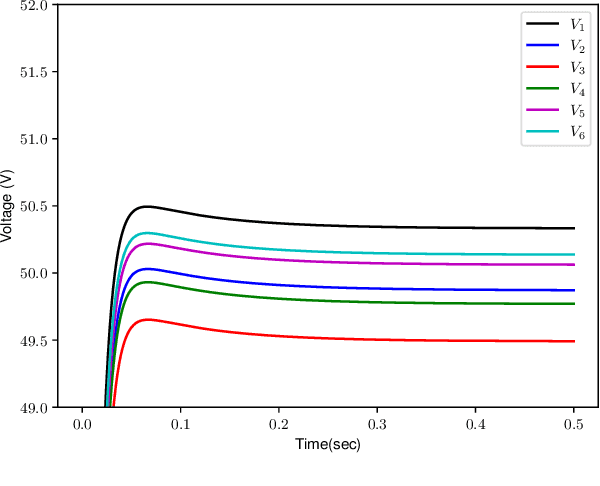
The control of large-scale cyber-physical systems requires optimal distributed policies relying solely on limited communication with neighboring agents. However, computing stabilizing controllers for nonlinear systems while optimizing complex costs remains a significant challenge. Neural Networks (NNs), known for their expressivity, can be leveraged to parametrize control policies that yield good performance. However, NNs' sensitivity to small input changes poses a risk of destabilizing the closed-loop system. Many existing approaches enforce constraints on the controllers' parameter space to guarantee closed-loop stability, leading to computationally expensive optimization procedures. To address these problems, we leverage the framework of port-Hamiltonian systems to design continuous-time distributed control policies for nonlinear systems that guarantee closed-loop stability and finite $\mathcal{L}_2$ or incremental $\mathcal{L}_2$ gains, independent of the optimzation parameters of the controllers. This eliminates the need to constrain parameters during optimization, allowing the use of standard techniques such as gradient-based methods. Additionally, we discuss discretization schemes that preserve the dissipation properties of these controllers for implementation on embedded systems. The effectiveness of the proposed distributed controllers is demonstrated through consensus control of non-holonomic mobile robots subject to collision avoidance and averaged voltage regulation with weighted power sharing in DC microgrids.

Maximum likelihood inference for high-dimensional problems with multiaffine variable relations

Maximum Likelihood Estimation of continuous variable models can be very challenging in high dimensions, due to potentially complex probability distributions. The existence of multiple interdependencies among variables can make it very difficult to establish convergence guarantees. This leads to a wide use of brute-force methods, such as grid searching and Monte-Carlo sampling and, when applicable, complex and problem-specific algorithms. In this paper, we consider inference problems where the variables are related by multiaffine expressions. We propose a novel Alternating and Iteratively-Reweighted Least Squares (AIRLS) algorithm, and prove its convergence for problems with Generalized Normal Distributions. We also provide an efficient method to compute the variance of the estimates obtained using AIRLS. Finally, we show how the method can be applied to graphical statistical models. We perform numerical experiments on several inference problems, showing significantly better performance than state-of-the-art approaches in terms of scalability, robustness to noise, and convergence speed due to an empirically observed super-linear convergence rate.

Learning to Boost the Performance of Stable Nonlinear Systems

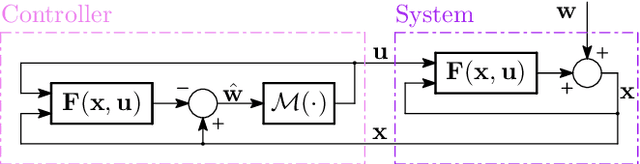
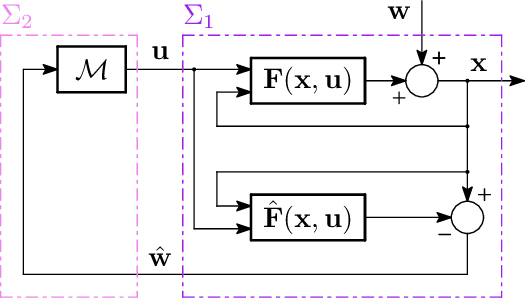
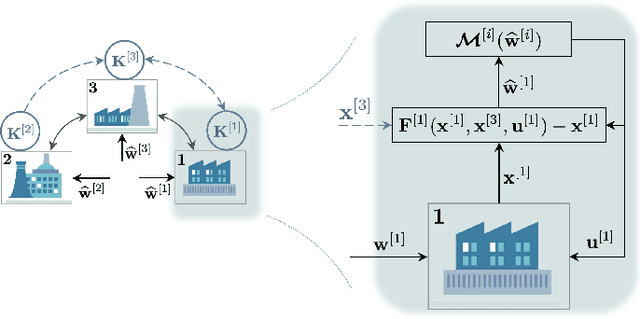
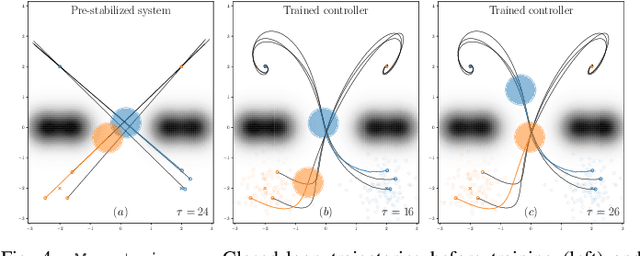
The growing scale and complexity of safety-critical control systems underscore the need to evolve current control architectures aiming for the unparalleled performances achievable through state-of-the-art optimization and machine learning algorithms. However, maintaining closed-loop stability while boosting the performance of nonlinear control systems using data-driven and deep-learning approaches stands as an important unsolved challenge. In this paper, we tackle the performance-boosting problem with closed-loop stability guarantees. Specifically, we establish a synergy between the Internal Model Control (IMC) principle for nonlinear systems and state-of-the-art unconstrained optimization approaches for learning stable dynamics. Our methods enable learning over arbitrarily deep neural network classes of performance-boosting controllers for stable nonlinear systems; crucially, we guarantee Lp closed-loop stability even if optimization is halted prematurely, and even when the ground-truth dynamics are unknown, with vanishing conservatism in the class of stabilizing policies as the model uncertainty is reduced to zero. We discuss the implementation details of the proposed control schemes, including distributed ones, along with the corresponding optimization procedures, demonstrating the potential of freely shaping the cost functions through several numerical experiments.

Unconstrained Parametrization of Dissipative and Contracting Neural Ordinary Differential Equations

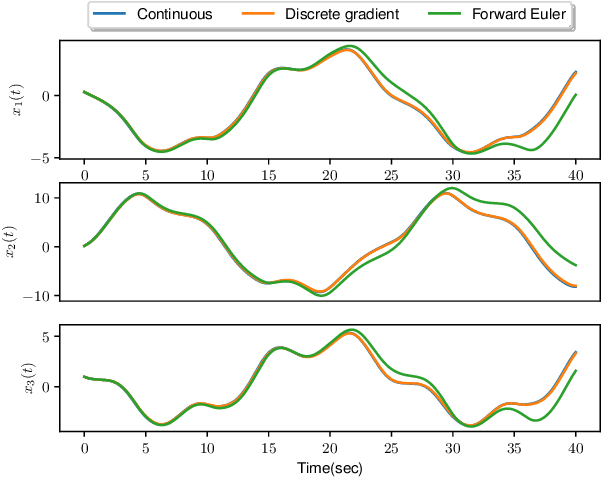
In this work, we introduce and study a class of Deep Neural Networks (DNNs) in continuous-time. The proposed architecture stems from the combination of Neural Ordinary Differential Equations (Neural ODEs) with the model structure of recently introduced Recurrent Equilibrium Networks (RENs). We show how to endow our proposed NodeRENs with contractivity and dissipativity -- crucial properties for robust learning and control. Most importantly, as for RENs, we derive parametrizations of contractive and dissipative NodeRENs which are unconstrained, hence enabling their learning for a large number of parameters. We validate the properties of NodeRENs, including the possibility of handling irregularly sampled data, in a case study in nonlinear system identification.

Universal Approximation Property of Hamiltonian Deep Neural Networks

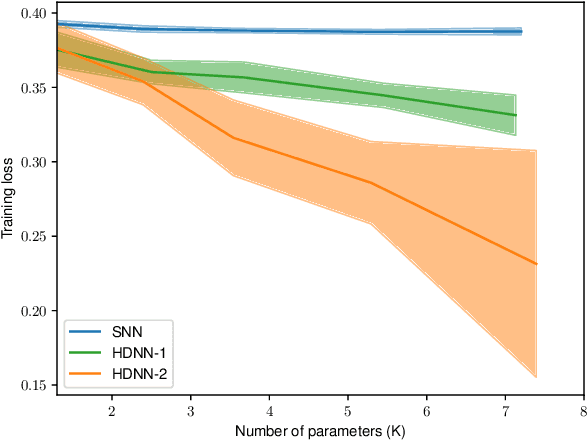
This paper investigates the universal approximation capabilities of Hamiltonian Deep Neural Networks (HDNNs) that arise from the discretization of Hamiltonian Neural Ordinary Differential Equations. Recently, it has been shown that HDNNs enjoy, by design, non-vanishing gradients, which provide numerical stability during training. However, although HDNNs have demonstrated state-of-the-art performance in several applications, a comprehensive study to quantify their expressivity is missing. In this regard, we provide a universal approximation theorem for HDNNs and prove that a portion of the flow of HDNNs can approximate arbitrary well any continuous function over a compact domain. This result provides a solid theoretical foundation for the practical use of HDNNs.

Follow the Clairvoyant: an Imitation Learning Approach to Optimal Control

We consider control of dynamical systems through the lens of competitive analysis. Most prior work in this area focuses on minimizing regret, that is, the loss relative to an ideal clairvoyant policy that has noncausal access to past, present, and future disturbances. Motivated by the observation that the optimal cost only provides coarse information about the ideal closed-loop behavior, we instead propose directly minimizing the tracking error relative to the optimal trajectories in hindsight, i.e., imitating the clairvoyant policy. By embracing a system level perspective, we present an efficient optimization-based approach for computing follow-the-clairvoyant (FTC) safe controllers. We prove that these attain minimal regret if no constraints are imposed on the noncausal benchmark. In addition, we present numerical experiments to show that our policy retains the hallmark of competitive algorithms of interpolating between classical $\mathcal{H}_2$ and $\mathcal{H}_\infty$ control laws - while consistently outperforming regret minimization methods in constrained scenarios thanks to the superior ability to chase the clairvoyant.

Robust online joint state/input/parameter estimation of linear systems

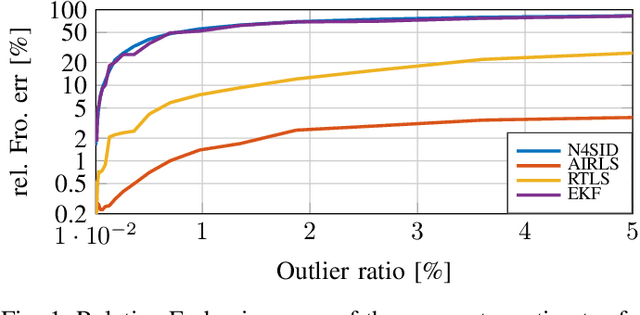
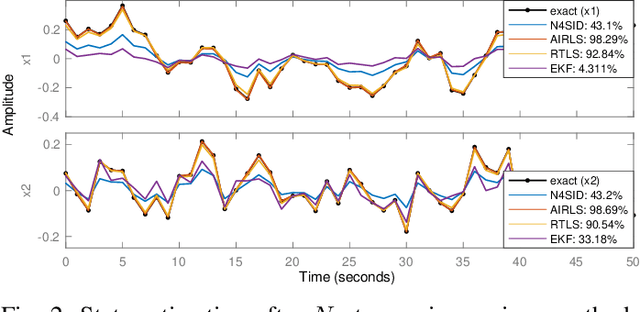
This paper presents a method for jointly estimating the state, input, and parameters of linear systems in an online fashion. The method is specially designed for measurements that are corrupted with non-Gaussian noise or outliers, which are commonly found in engineering applications. In particular, it combines recursive, alternating, and iteratively-reweighted least squares into a single, one-step algorithm, which solves the estimation problem online and benefits from the robustness of least-deviation regression methods. The convergence of the iterative method is formally guaranteed. Numerical experiments show the good performance of the estimation algorithm in presence of outliers and in comparison to state-of-the-art methods.

Neural System Level Synthesis: Learning over All Stabilizing Policies for Nonlinear Systems

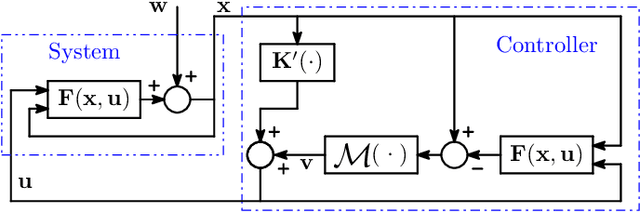
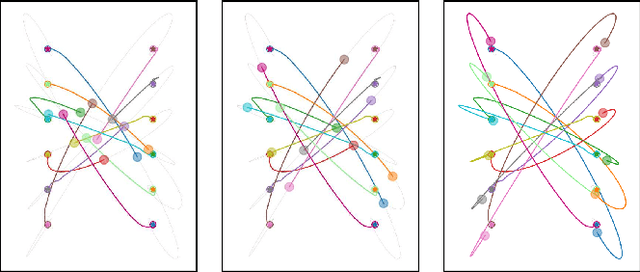
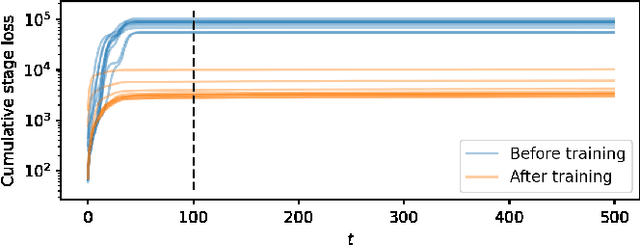
We address the problem of designing stabilizing control policies for nonlinear systems in discrete-time, while minimizing an arbitrary cost function. When the system is linear and the cost is convex, the System Level Synthesis (SLS) approach offers an exact solution based on convex programming. Beyond this case, a globally optimal solution cannot be found in a tractable way, in general. In this paper, we develop a parametrization of all and only the control policies stabilizing a given time-varying nonlinear system in terms of the combined effect of 1) a strongly stabilizing base controller and 2) a stable SLS operator to be freely designed. Based on this result, we propose a Neural SLS (Neur-SLS) approach guaranteeing closed-loop stability during and after parameter optimization, without requiring any constraints to be satisfied. We exploit recent Deep Neural Network (DNN) models based on Recurrent Equilibrium Networks (RENs) to learn over a rich class of nonlinear stable operators, and demonstrate the effectiveness of the proposed approach in numerical examples.