Contractive Dynamical Imitation Policies for Efficient Out-of-Sample Recovery

Imitation learning is a data-driven approach to learning policies from expert behavior, but it is prone to unreliable outcomes in out-of-sample (OOS) regions. While previous research relying on stable dynamical systems guarantees convergence to a desired state, it often overlooks transient behavior. We propose a framework for learning policies using modeled by contractive dynamical systems, ensuring that all policy rollouts converge regardless of perturbations, and in turn, enable efficient OOS recovery. By leveraging recurrent equilibrium networks and coupling layers, the policy structure guarantees contractivity for any parameter choice, which facilitates unconstrained optimization. Furthermore, we provide theoretical upper bounds for worst-case and expected loss terms, rigorously establishing the reliability of our method in deployment. Empirically, we demonstrate substantial OOS performance improvements in robotics manipulation and navigation tasks in simulation.

Single-Shot Learning of Stable Dynamical Systems for Long-Horizon Manipulation Tasks

Mastering complex sequential tasks continues to pose a significant challenge in robotics. While there has been progress in learning long-horizon manipulation tasks, most existing approaches lack rigorous mathematical guarantees for ensuring reliable and successful execution. In this paper, we extend previous work on learning long-horizon tasks and stable policies, focusing on improving task success rates while reducing the amount of training data needed. Our approach introduces a novel method that (1) segments long-horizon demonstrations into discrete steps defined by waypoints and subgoals, and (2) learns globally stable dynamical system policies to guide the robot to each subgoal, even in the face of sensory noise and random disturbances. We validate our approach through both simulation and real-world experiments, demonstrating effective transfer from simulation to physical robotic platforms. Code is available at https://github.com/Alestaubin/stable-imitation-policy-with-waypoints

Globally Stable Neural Imitation Policies

Imitation learning presents an effective approach to alleviate the resource-intensive and time-consuming nature of policy learning from scratch in the solution space. Even though the resulting policy can mimic expert demonstrations reliably, it often lacks predictability in unexplored regions of the state-space, giving rise to significant safety concerns in the face of perturbations. To address these challenges, we introduce the Stable Neural Dynamical System (SNDS), an imitation learning regime which produces a policy with formal stability guarantees. We deploy a neural policy architecture that facilitates the representation of stability based on Lyapunov theorem, and jointly train the policy and its corresponding Lyapunov candidate to ensure global stability. We validate our approach by conducting extensive experiments in simulation and successfully deploying the trained policies on a real-world manipulator arm. The experimental results demonstrate that our method overcomes the instability, accuracy, and computational intensity problems associated with previous imitation learning methods, making our method a promising solution for stable policy learning in complex planning scenarios.

Learning Lyapunov-Stable Polynomial Dynamical Systems Through Imitation

Imitation learning is a paradigm to address complex motion planning problems by learning a policy to imitate an expert's behavior. However, relying solely on the expert's data might lead to unsafe actions when the robot deviates from the demonstrated trajectories. Stability guarantees have previously been provided utilizing nonlinear dynamical systems, acting as high-level motion planners, in conjunction with the Lyapunov stability theorem. Yet, these methods are prone to inaccurate policies, high computational cost, sample inefficiency, or quasi stability when replicating complex and highly nonlinear trajectories. To mitigate this problem, we present an approach for learning a globally stable nonlinear dynamical system as a motion planning policy. We model the nonlinear dynamical system as a parametric polynomial and learn the polynomial's coefficients jointly with a Lyapunov candidate. To showcase its success, we compare our method against the state of the art in simulation and conduct real-world experiments with the Kinova Gen3 Lite manipulator arm. Our experiments demonstrate the sample efficiency and reproduction accuracy of our method for various expert trajectories, while remaining stable in the face of perturbations.

FED-CD: Federated Causal Discovery from Interventional and Observational Data

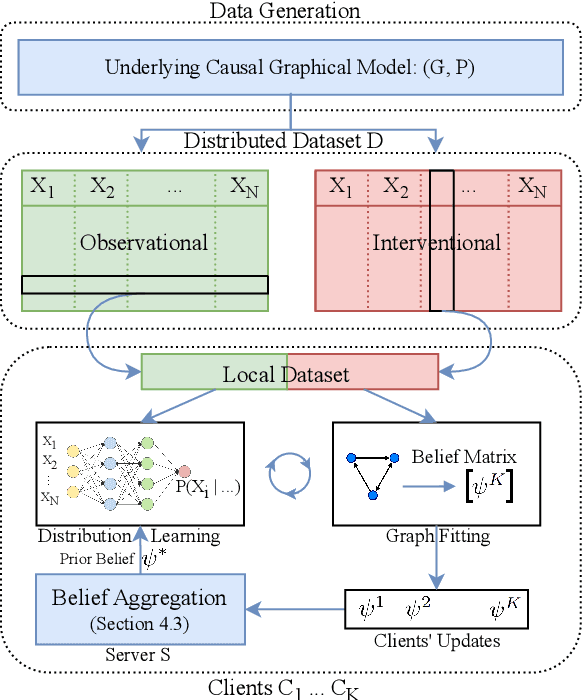
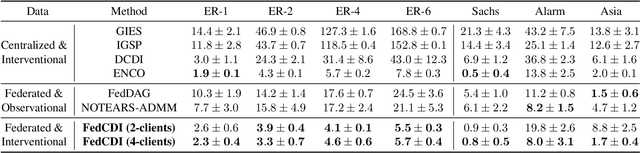
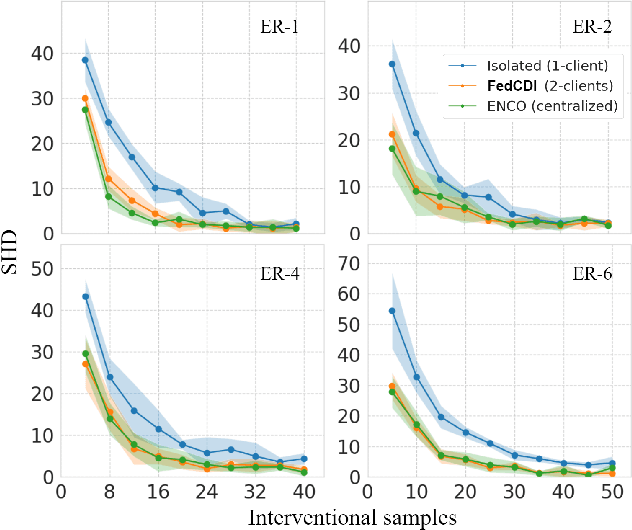
Causal discovery, the inference of causal relations from data, is a core task of fundamental importance in all scientific domains, and several new machine learning methods for addressing the causal discovery problem have been proposed recently. However, existing machine learning methods for causal discovery typically require that the data used for inference is pooled and available in a centralized location. In many domains of high practical importance, such as in healthcare, data is only available at local data-generating entities (e.g. hospitals in the healthcare context), and cannot be shared across entities due to, among others, privacy and regulatory reasons. In this work, we address the problem of inferring causal structure - in the form of a directed acyclic graph (DAG) - from a distributed data set that contains both observational and interventional data in a privacy-preserving manner by exchanging updates instead of samples. To this end, we introduce a new federated framework, FED-CD, that enables the discovery of global causal structures both when the set of intervened covariates is the same across decentralized entities, and when the set of intervened covariates are potentially disjoint. We perform a comprehensive experimental evaluation on synthetic data that demonstrates that FED-CD enables effective aggregation of decentralized data for causal discovery without direct sample sharing, even when the contributing distributed data sets cover disjoint sets of interventions. Effective methods for causal discovery in distributed data sets could significantly advance scientific discovery and knowledge sharing in important settings, for instance, healthcare, in which sharing of data across local sites is difficult or prohibited.

Pyfectious: An individual-level simulator to discover optimal containment polices for epidemic diseases

Simulating the spread of infectious diseases in human communities is critical for predicting the trajectory of an epidemic and verifying various policies to control the devastating impacts of the outbreak. Many existing simulators are based on compartment models that divide people into a few subsets and simulate the dynamics among those subsets using hypothesized differential equations. However, these models lack the requisite granularity to study the effect of intelligent policies that influence every individual in a particular way. In this work, we introduce a simulator software capable of modeling a population structure and controlling the disease's propagation at an individualistic level. In order to estimate the confidence of the conclusions drawn from the simulator, we employ a comprehensive probabilistic approach where the entire population is constructed as a hierarchical random variable. This approach makes the inferred conclusions more robust against sampling artifacts and gives confidence bounds for decisions based on the simulation results. To showcase potential applications, the simulator parameters are set based on the formal statistics of the COVID-19 pandemic, and the outcome of a wide range of control measures is investigated. Furthermore, the simulator is used as the environment of a reinforcement learning problem to find the optimal policies to control the pandemic. The obtained experimental results indicate the simulator's adaptability and capacity in making sound predictions and a successful policy derivation example based on real-world data. As an exemplary application, our results show that the proposed policy discovery method can lead to control measures that produce significantly fewer infected individuals in the population and protect the health system against saturation.