Double Machine Learning for Conditional Moment Restrictions: IV regression, Proximal Causal Learning and Beyond

Solving conditional moment restrictions (CMRs) is a key problem considered in statistics, causal inference, and econometrics, where the aim is to solve for a function of interest that satisfies some conditional moment equalities. Specifically, many techniques for causal inference, such as instrumental variable (IV) regression and proximal causal learning (PCL), are CMR problems. Most CMR estimators use a two-stage approach, where the first-stage estimation is directly plugged into the second stage to estimate the function of interest. However, naively plugging in the first-stage estimator can cause heavy bias in the second stage. This is particularly the case for recently proposed CMR estimators that use deep neural network (DNN) estimators for both stages, where regularisation and overfitting bias is present. We propose DML-CMR, a two-stage CMR estimator that provides an unbiased estimate with fast convergence rate guarantees. We derive a novel learning objective to reduce bias and develop the DML-CMR algorithm following the double/debiased machine learning (DML) framework. We show that our DML-CMR estimator can achieve the minimax optimal convergence rate of $O(N^{-1/2})$ under parameterisation and mild regularity conditions, where $N$ is the sample size. We apply DML-CMR to a range of problems using DNN estimators, including IV regression and proximal causal learning on real-world datasets, demonstrating state-of-the-art performance against existing CMR estimators and algorithms tailored to those problems.

Cautious Optimism: A Meta-Algorithm for Near-Constant Regret in General Games

Recent work [Soleymani et al., 2025] introduced a variant of Optimistic Multiplicative Weights Updates (OMWU) that adaptively controls the learning pace in a dynamic, non-monotone manner, achieving new state-of-the-art regret minimization guarantees in general games. In this work, we demonstrate that no-regret learning acceleration through adaptive pacing of the learners is not an isolated phenomenon. We introduce \emph{Cautious Optimism}, a framework for substantially faster regularized learning in general games. Cautious Optimism takes as input any instance of Follow-the-Regularized-Leader (FTRL) and outputs an accelerated no-regret learning algorithm by pacing the underlying FTRL with minimal computational overhead. Importantly, we retain uncoupledness (learners do not need to know other players' utilities). Cautious Optimistic FTRL achieves near-optimal $O_T(\log T)$ regret in diverse self-play (mixing-and-matching regularizers) while preserving the optimal $O(\sqrt{T})$ regret in adversarial scenarios. In contrast to prior works (e.g. Syrgkanis et al. [2015], Daskalakis et al. [2021]), our analysis does not rely on monotonic step-sizes, showcasing a novel route for fast learning in general games.

Faster Rates for No-Regret Learning in General Games via Cautious Optimism

We establish the first uncoupled learning algorithm that attains $O(n \log^2 d \log T)$ per-player regret in multi-player general-sum games, where $n$ is the number of players, $d$ is the number of actions available to each player, and $T$ is the number of repetitions of the game. Our results exponentially improve the dependence on $d$ compared to the $O(n\, d \log T)$ regret attainable by Log-Regularized Lifted Optimistic FTRL [Far+22c], and also reduce the dependence on the number of iterations $T$ from $\log^4 T$ to $\log T$ compared to Optimistic Hedge, the previously well-studied algorithm with $O(n \log d \log^4 T)$ regret [DFG21]. Our algorithm is obtained by combining the classic Optimistic Multiplicative Weights Update (OMWU) with an adaptive, non-monotonic learning rate that paces the learning process of the players, making them more cautious when their regret becomes too negative.

Learning with Exact Invariances in Polynomial Time

We study the statistical-computational trade-offs for learning with exact invariances (or symmetries) using kernel regression. Traditional methods, such as data augmentation, group averaging, canonicalization, and frame-averaging, either fail to provide a polynomial-time solution or are not applicable in the kernel setting. However, with oracle access to the geometric properties of the input space, we propose a polynomial-time algorithm that learns a classifier with \emph{exact} invariances. Moreover, our approach achieves the same excess population risk (or generalization error) as the original kernel regression problem. To the best of our knowledge, this is the first polynomial-time algorithm to achieve exact (not approximate) invariances in this context. Our proof leverages tools from differential geometry, spectral theory, and optimization. A key result in our development is a new reformulation of the problem of learning under invariances as optimizing an infinite number of linearly constrained convex quadratic programs, which may be of independent interest.

A Universal Class of Sharpness-Aware Minimization Algorithms

Recently, there has been a surge in interest in developing optimization algorithms for overparameterized models as achieving generalization is believed to require algorithms with suitable biases. This interest centers on minimizing sharpness of the original loss function; the Sharpness-Aware Minimization (SAM) algorithm has proven effective. However, most literature only considers a few sharpness measures, such as the maximum eigenvalue or trace of the training loss Hessian, which may not yield meaningful insights for non-convex optimization scenarios like neural networks. Additionally, many sharpness measures are sensitive to parameter invariances in neural networks, magnifying significantly under rescaling parameters. Motivated by these challenges, we introduce a new class of sharpness measures in this paper, leading to new sharpness-aware objective functions. We prove that these measures are \textit{universally expressive}, allowing any function of the training loss Hessian matrix to be represented by appropriate hyperparameters. Furthermore, we show that the proposed objective functions explicitly bias towards minimizing their corresponding sharpness measures, and how they allow meaningful applications to models with parameter invariances (such as scale-invariances). Finally, as instances of our proposed general framework, we present \textit{Frob-SAM} and \textit{Det-SAM}, which are specifically designed to minimize the Frobenius norm and the determinant of the Hessian of the training loss, respectively. We also demonstrate the advantages of our general framework through extensive experiments.

Learning Decision Policies with Instrumental Variables through Double Machine Learning

A common issue in learning decision-making policies in data-rich settings is spurious correlations in the offline dataset, which can be caused by hidden confounders. Instrumental variable (IV) regression, which utilises a key unconfounded variable known as the instrument, is a standard technique for learning causal relationships between confounded action, outcome, and context variables. Most recent IV regression algorithms use a two-stage approach, where a deep neural network (DNN) estimator learnt in the first stage is directly plugged into the second stage, in which another DNN is used to estimate the causal effect. Naively plugging the estimator can cause heavy bias in the second stage, especially when regularisation bias is present in the first stage estimator. We propose DML-IV, a non-linear IV regression method that reduces the bias in two-stage IV regressions and effectively learns high-performing policies. We derive a novel learning objective to reduce bias and design the DML-IV algorithm following the double/debiased machine learning (DML) framework. The learnt DML-IV estimator has strong convergence rate and $O(N^{-1/2})$ suboptimality guarantees that match those when the dataset is unconfounded. DML-IV outperforms state-of-the-art IV regression methods on IV regression benchmarks and learns high-performing policies in the presence of instruments.

Doubly Robust Structure Identification from Temporal Data

Learning the causes of time-series data is a fundamental task in many applications, spanning from finance to earth sciences or bio-medical applications. Common approaches for this task are based on vector auto-regression, and they do not take into account unknown confounding between potential causes. However, in settings with many potential causes and noisy data, these approaches may be substantially biased. Furthermore, potential causes may be correlated in practical applications. Moreover, existing algorithms often do not work with cyclic data. To address these challenges, we propose a new doubly robust method for Structure Identification from Temporal Data ( SITD ). We provide theoretical guarantees, showing that our method asymptotically recovers the true underlying causal structure. Our analysis extends to cases where the potential causes have cycles and they may be confounded. We further perform extensive experiments to showcase the superior performance of our method.

DRCFS: Doubly Robust Causal Feature Selection

Knowing the features of a complex system that are highly relevant to a particular target variable is of fundamental interest in many areas of science. Existing approaches are often limited to linear settings, sometimes lack guarantees, and in most cases, do not scale to the problem at hand, in particular to images. We propose DRCFS, a doubly robust feature selection method for identifying the causal features even in nonlinear and high dimensional settings. We provide theoretical guarantees, illustrate necessary conditions for our assumptions, and perform extensive experiments across a wide range of simulated and semi-synthetic datasets. DRCFS significantly outperforms existing state-of-the-art methods, selecting robust features even in challenging highly non-linear and high-dimensional problems.

Federated Learning in Multi-Center Critical Care Research: A Systematic Case Study using the eICU Database

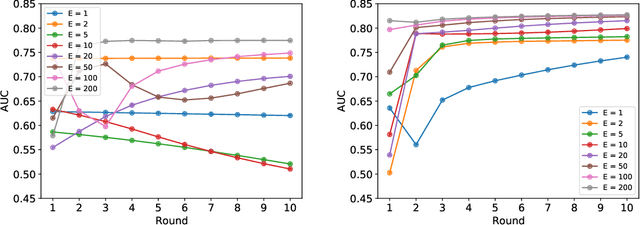
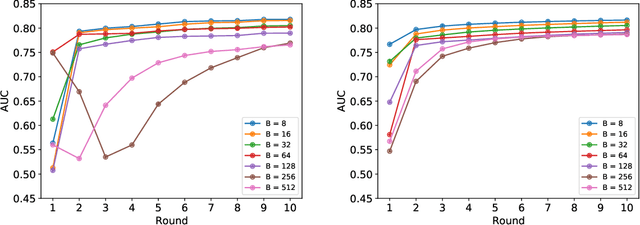
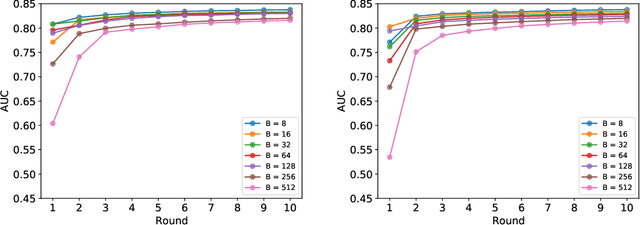
Federated learning (FL) has been proposed as a method to train a model on different units without exchanging data. This offers great opportunities in the healthcare sector, where large datasets are available but cannot be shared to ensure patient privacy. We systematically investigate the effectiveness of FL on the publicly available eICU dataset for predicting the survival of each ICU stay. We employ Federated Averaging as the main practical algorithm for FL and show how its performance changes by altering three key hyper-parameters, taking into account that clients can significantly vary in size. We find that in many settings, a large number of local training epochs improves the performance while at the same time reducing communication costs. Furthermore, we outline in which settings it is possible to have only a low number of hospitals participating in each federated update round. When many hospitals with low patient counts are involved, the effect of overfitting can be avoided by decreasing the batchsize. This study thus contributes toward identifying suitable settings for running distributed algorithms such as FL on clinical datasets.

Physical Derivatives: Computing policy gradients by physical forward-propagation

Model-free and model-based reinforcement learning are two ends of a spectrum. Learning a good policy without a dynamic model can be prohibitively expensive. Learning the dynamic model of a system can reduce the cost of learning the policy, but it can also introduce bias if it is not accurate. We propose a middle ground where instead of the transition model, the sensitivity of the trajectories with respect to the perturbation of the parameters is learned. This allows us to predict the local behavior of the physical system around a set of nominal policies without knowing the actual model. We assay our method on a custom-built physical robot in extensive experiments and show the feasibility of the approach in practice. We investigate potential challenges when applying our method to physical systems and propose solutions to each of them.