A Metropolis-Adjusted Langevin Algorithm for Sampling Jeffreys Prior

Inference and estimation are fundamental aspects of statistics, system identification and machine learning. For most inference problems, prior knowledge is available on the system to be modeled, and Bayesian analysis is a natural framework to impose such prior information in the form of a prior distribution. However, in many situations, coming out with a fully specified prior distribution is not easy, as prior knowledge might be too vague, so practitioners prefer to use a prior distribution that is as `ignorant' or `uninformative' as possible, in the sense of not imposing subjective beliefs, while still supporting reliable statistical analysis. Jeffreys prior is an appealing uninformative prior because it offers two important benefits: (i) it is invariant under any re-parameterization of the model, (ii) it encodes the intrinsic geometric structure of the parameter space through the Fisher information matrix, which in turn enhances the diversity of parameter samples. Despite these benefits, drawing samples from Jeffreys prior is a challenging task. In this paper, we propose a general sampling scheme using the Metropolis-Adjusted Langevin Algorithm that enables sampling of parameter values from Jeffreys prior, and provide numerical illustrations of our approach through several examples.

Kernel-based learning with guarantees for multi-agent applications

This paper addresses a kernel-based learning problem for a network of agents locally observing a latent multidimensional, nonlinear phenomenon in a noisy environment. We propose a learning algorithm that requires only mild a priori knowledge about the phenomenon under investigation and delivers a model with corresponding non-asymptotic high probability error bounds. Both non-asymptotic analysis of the method and numerical simulation results are presented and discussed in the paper.

Unraveling the Control Engineer's Craft with Neural Networks

Many industrial processes require suitable controllers to meet their performance requirements. More often, a sophisticated digital twin is available, which is a highly complex model that is a virtual representation of a given physical process, whose parameters may not be properly tuned to capture the variations in the physical process. In this paper, we present a sim2real, direct data-driven controller tuning approach, where the digital twin is used to generate input-output data and suitable controllers for several perturbations in its parameters. State-of-the art neural-network architectures are then used to learn the controller tuning rule that maps input-output data onto the controller parameters, based on artificially generated data from perturbed versions of the digital twin. In this way, as far as we are aware, we tackle for the first time the problem of re-calibrating the controller by meta-learning the tuning rule directly from data, thus practically replacing the control engineer with a machine learning model. The benefits of this methodology are illustrated via numerical simulations for several choices of neural-network architectures.

DRCFS: Doubly Robust Causal Feature Selection

Knowing the features of a complex system that are highly relevant to a particular target variable is of fundamental interest in many areas of science. Existing approaches are often limited to linear settings, sometimes lack guarantees, and in most cases, do not scale to the problem at hand, in particular to images. We propose DRCFS, a doubly robust feature selection method for identifying the causal features even in nonlinear and high dimensional settings. We provide theoretical guarantees, illustrate necessary conditions for our assumptions, and perform extensive experiments across a wide range of simulated and semi-synthetic datasets. DRCFS significantly outperforms existing state-of-the-art methods, selecting robust features even in challenging highly non-linear and high-dimensional problems.

Decentralized diffusion-based learning under non-parametric limited prior knowledge

We study the problem of diffusion-based network learning of a nonlinear phenomenon, $m$, from local agents' measurements collected in a noisy environment. For a decentralized network and information spreading merely between directly neighboring nodes, we propose a non-parametric learning algorithm, that avoids raw data exchange and requires only mild \textit{a priori} knowledge about $m$. Non-asymptotic estimation error bounds are derived for the proposed method. Its potential applications are illustrated through simulation experiments.

Diagnosing and Augmenting Feature Representations in Correctional Inverse Reinforcement Learning

Robots have been increasingly better at doing tasks for humans by learning from their feedback, but still often suffer from model misalignment due to missing or incorrectly learned features. When the features the robot needs to learn to perform its task are missing or do not generalize well to new settings, the robot will not be able to learn the task the human wants and, even worse, may learn a completely different and undesired behavior. Prior work shows how the robot can detect when its representation is missing some feature and can, thus, ask the human to be taught about the new feature; however, these works do not differentiate between features that are completely missing and those that exist but do not generalize to new environments. In the latter case, the robot would detect misalignment and simply learn a new feature, leading to an arbitrarily growing feature representation that can, in turn, lead to spurious correlations and incorrect learning down the line. In this work, we propose separating the two sources of misalignment: we propose a framework for determining whether a feature the robot needs is incorrectly learned and does not generalize to new environment setups vs. is entirely missing from the robot's representation. Once we detect the source of error, we show how the human can initiate the realignment process for the model: if the feature is missing, we follow prior work for learning new features; however, if the feature exists but does not generalize, we use data augmentation to expand its training and, thus, complete the correction. We demonstrate the proposed approach in experiments with a simulated 7DoF robot manipulator and physical human corrections.

Optimal Transport for Correctional Learning

The contribution of this paper is a generalized formulation of correctional learning using optimal transport, which is about how to optimally transport one mass distribution to another. Correctional learning is a framework developed to enhance the accuracy of parameter estimation processes by means of a teacher-student approach. In this framework, an expert agent, referred to as the teacher, modifies the data used by a learning agent, known as the student, to improve its estimation process. The objective of the teacher is to alter the data such that the student's estimation error is minimized, subject to a fixed intervention budget. Compared to existing formulations of correctional learning, our novel optimal transport approach provides several benefits. It allows for the estimation of more complex characteristics as well as the consideration of multiple intervention policies for the teacher. We evaluate our approach on two theoretical examples, and on a human-robot interaction application in which the teacher's role is to improve the robots performance in an inverse reinforcement learning setting.

A Unified Approach to Differentially Private Bayes Point Estimation

Parameter estimation in statistics and system identification relies on data that may contain sensitive information. To protect this sensitive information, the notion of \emph{differential privacy} (DP) has been proposed, which enforces confidentiality by introducing randomization in the estimates. Standard algorithms for differentially private estimation are based on adding an appropriate amount of noise to the output of a traditional point estimation method. This leads to an accuracy-privacy trade off, as adding more noise reduces the accuracy while increasing privacy. In this paper, we propose a new Unified Bayes Private Point (UBaPP) approach to Bayes point estimation of the unknown parameters of a data generating mechanism under a DP constraint, that achieves a better accuracy-privacy trade off than traditional approaches. We verify the performance of our approach on a simple numerical example.

A Statistical Decision-Theoretical Perspective on the Two-Stage Approach to Parameter Estimation

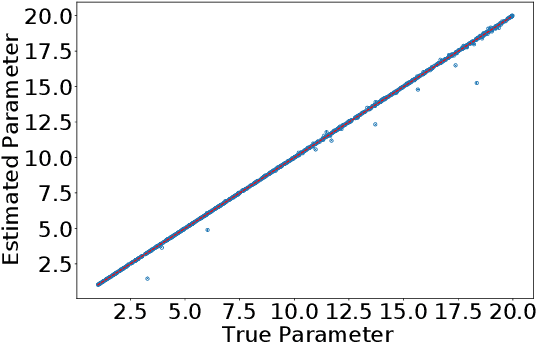
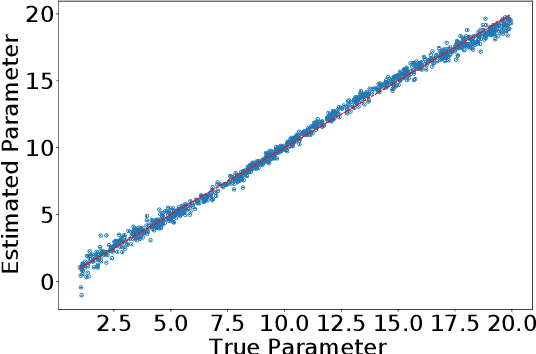
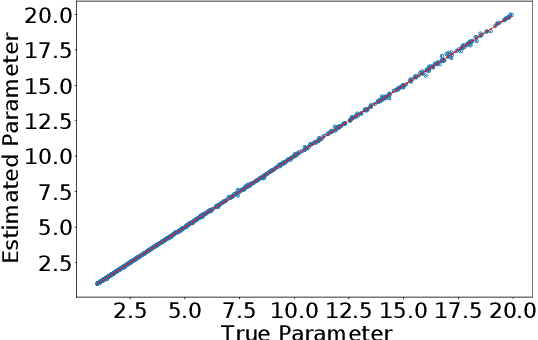
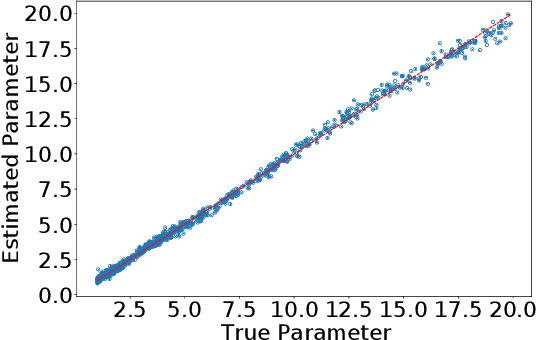
One of the most important problems in system identification and statistics is how to estimate the unknown parameters of a given model. Optimization methods and specialized procedures, such as Empirical Minimization (EM) can be used in case the likelihood function can be computed. For situations where one can only simulate from a parametric model, but the likelihood is difficult or impossible to evaluate, a technique known as the Two-Stage (TS) Approach can be applied to obtain reliable parametric estimates. Unfortunately, there is currently a lack of theoretical justification for TS. In this paper, we propose a statistical decision-theoretical derivation of TS, which leads to Bayesian and Minimax estimators. We also show how to apply the TS approach on models for independent and identically distributed samples, by computing quantiles of the data as a first step, and using a linear function as the second stage. The proposed method is illustrated via numerical simulations.

A teacher-student framework for online correctional learning

A classical learning setting is one in which a student collects data, or observations, about a system, and estimates a certain quantity of interest about it. Correctional learning is a type of cooperative teacher-student framework where a teacher, who has knowledge about the system, has the possibility to observe and alter (correct) the observations received by the student in order to improve its estimation. In this paper, we show that the variance of the estimate of the student is reduced with the help of the teacher. We further formulate the online problem - where the teacher has to decide at each time instant whether or not to change the observations - as a Markov decision process, from which the optimal policy is derived using dynamic programming. We validate the framework in numerical experiments, and compare the optimal online policy with the one from the batch setting.