Computationally lightweight classifiers with frequentist bounds on predictions

While both classical and neural network classifiers can achieve high accuracy, they fall short on offering uncertainty bounds on their predictions, making them unfit for safety-critical applications. Existing kernel-based classifiers that provide such bounds scale with $\mathcal O (n^{\sim3})$ in time, making them computationally intractable for large datasets. To address this, we propose a novel, computationally efficient classification algorithm based on the Nadaraya-Watson estimator, for whose estimates we derive frequentist uncertainty intervals. We evaluate our classifier on synthetically generated data and on electrocardiographic heartbeat signals from the MIT-BIH Arrhythmia database. We show that the method achieves competitive accuracy $>$\SI{96}{\percent} at $\mathcal O(n)$ and $\mathcal O(\log n)$ operations, while providing actionable uncertainty bounds. These bounds can, e.g., aid in flagging low-confidence predictions, making them suitable for real-time settings with resource constraints, such as diagnostic monitoring or implantable devices.

Ergodicity in reinforcement learning

In reinforcement learning, we typically aim to optimize the expected value of the sum of rewards an agent collects over a trajectory. However, if the process generating these rewards is non-ergodic, the expected value, i.e., the average over infinitely many trajectories with a given policy, is uninformative for the average over a single, but infinitely long trajectory. Thus, if we care about how the individual agent performs during deployment, the expected value is not a good optimization objective. In this paper, we discuss the impact of non-ergodic reward processes on reinforcement learning agents through an instructive example, relate the notion of ergodic reward processes to more widely used notions of ergodic Markov chains, and present existing solutions that optimize long-term performance of individual trajectories under non-ergodic reward dynamics.

Integrating Lagrangian Neural Networks into the Dyna Framework for Reinforcement Learning

Model-based reinforcement learning (MBRL) is sample-efficient but depends on the accuracy of the learned dynamics, which are often modeled using black-box methods that do not adhere to physical laws. Those methods tend to produce inaccurate predictions when presented with data that differ from the original training set. In this work, we employ Lagrangian neural networks (LNNs), which enforce an underlying Lagrangian structure to train the model within a Dyna-based MBRL framework. Furthermore, we train the LNN using stochastic gradient-based and state-estimation-based optimizers to learn the network's weights. The state-estimation-based method converges faster than the stochastic gradient-based method during neural network training. Simulation results are provided to illustrate the effectiveness of the proposed LNN-based Dyna framework for MBRL.

Safe Bayesian optimization across noise models via scenario programming

Safe Bayesian optimization (BO) with Gaussian processes is an effective tool for tuning control policies in safety-critical real-world systems, specifically due to its sample efficiency and safety guarantees. However, most safe BO algorithms assume homoscedastic sub-Gaussian measurement noise, an assumption that does not hold in many relevant applications. In this article, we propose a straightforward yet rigorous approach for safe BO across noise models, including homoscedastic sub-Gaussian and heteroscedastic heavy-tailed distributions. We provide a high-probability bound on the measurement noise via the scenario approach, integrate these bounds into high probability confidence intervals, and prove safety and optimality for our proposed safe BO algorithm. We deploy our algorithm in synthetic examples and in tuning a controller for the Franka Emika manipulator in simulation.

Online Bayesian Experimental Design for Partially Observed Dynamical Systems

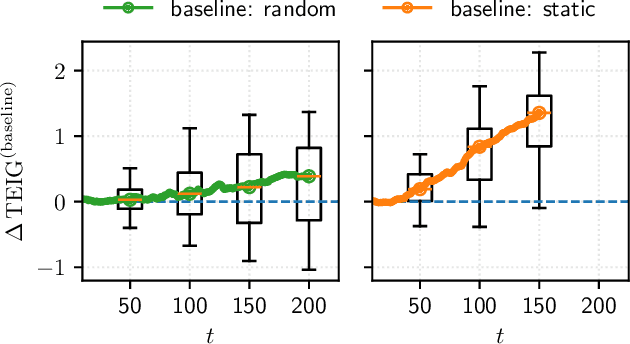
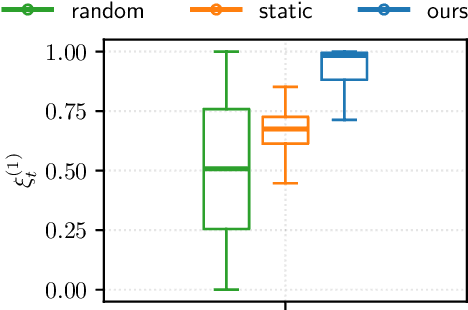
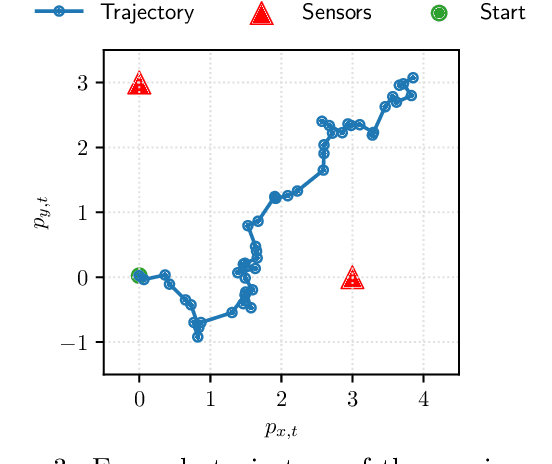
Bayesian experimental design (BED) provides a principled framework for optimizing data collection, but existing approaches do not apply to crucial real-world settings such as dynamical systems with partial observability, where only noisy and incomplete observations are available. These systems are naturally modeled as state-space models (SSMs), where latent states mediate the link between parameters and data, making the likelihood -- and thus information-theoretic objectives like the expected information gain (EIG) -- intractable. In addition, the dynamical nature of the system requires online algorithms that update posterior distributions and select designs sequentially in a computationally efficient manner. We address these challenges by deriving new estimators of the EIG and its gradient that explicitly marginalize latent states, enabling scalable stochastic optimization in nonlinear SSMs. Our approach leverages nested particle filters (NPFs) for efficient online inference with convergence guarantees. Applications to realistic models, such as the susceptible-infected-recovered (SIR) and a moving source location task, show that our framework successfully handles both partial observability and online computation.

A Lightweight Crowd Model for Robot Social Navigation

Robots operating in human-populated environments must navigate safely and efficiently while minimizing social disruption. Achieving this requires estimating crowd movement to avoid congested areas in real-time. Traditional microscopic models struggle to scale in dense crowds due to high computational cost, while existing macroscopic crowd prediction models tend to be either overly simplistic or computationally intensive. In this work, we propose a lightweight, real-time macroscopic crowd prediction model tailored for human motion, which balances prediction accuracy and computational efficiency. Our approach simplifies both spatial and temporal processing based on the inherent characteristics of pedestrian flow, enabling robust generalization without the overhead of complex architectures. We demonstrate a 3.6 times reduction in inference time, while improving prediction accuracy by 3.1 %. Integrated into a socially aware planning framework, the model enables efficient and socially compliant robot navigation in dynamic environments. This work highlights that efficient human crowd modeling enables robots to navigate dense environments without costly computations.

Efficient Human-Aware Task Allocation for Multi-Robot Systems in Shared Environments

Multi-robot systems are increasingly deployed in applications, such as intralogistics or autonomous delivery, where multiple robots collaborate to complete tasks efficiently. One of the key factors enabling their efficient cooperation is Multi-Robot Task Allocation (MRTA). Algorithms solving this problem optimize task distribution among robots to minimize the overall execution time. In shared environments, apart from the relative distance between the robots and the tasks, the execution time is also significantly impacted by the delay caused by navigating around moving people. However, most existing MRTA approaches are dynamics-agnostic, relying on static maps and neglecting human motion patterns, leading to inefficiencies and delays. In this paper, we introduce \acrfull{method name}. This method leverages Maps of Dynamics (MoDs), spatio-temporal queryable models designed to capture historical human movement patterns, to estimate the impact of humans on the task execution time during deployment. \acrshort{method name} utilizes a stochastic cost function that includes MoDs. Experimental results show that integrating MoDs enhances task allocation performance, resulting in reduced mission completion times by up to $26\%$ compared to the dynamics-agnostic method and up to $19\%$ compared to the baseline. This work underscores the importance of considering human dynamics in MRTA within shared environments and presents an efficient framework for deploying multi-robot systems in environments populated by humans.

Safety and optimality in learning-based control at low computational cost

Applying machine learning methods to physical systems that are supposed to act in the real world requires providing safety guarantees. However, methods that include such guarantees often come at a high computational cost, making them inapplicable to large datasets and embedded devices with low computational power. In this paper, we propose CoLSafe, a computationally lightweight safe learning algorithm whose computational complexity grows sublinearly with the number of data points. We derive both safety and optimality guarantees and showcase the effectiveness of our algorithm on a seven-degrees-of-freedom robot arm.

Safe exploration in reproducing kernel Hilbert spaces

Popular safe Bayesian optimization (BO) algorithms learn control policies for safety-critical systems in unknown environments. However, most algorithms make a smoothness assumption, which is encoded by a known bounded norm in a reproducing kernel Hilbert space (RKHS). The RKHS is a potentially infinite-dimensional space, and it remains unclear how to reliably obtain the RKHS norm of an unknown function. In this work, we propose a safe BO algorithm capable of estimating the RKHS norm from data. We provide statistical guarantees on the RKHS norm estimation, integrate the estimated RKHS norm into existing confidence intervals and show that we retain theoretical guarantees, and prove safety of the resulting safe BO algorithm. We apply our algorithm to safely optimize reinforcement learning policies on physics simulators and on a real inverted pendulum, demonstrating improved performance, safety, and scalability compared to the state-of-the-art.

Transfer Learning in Latent Contextual Bandits with Covariate Shift Through Causal Transportability

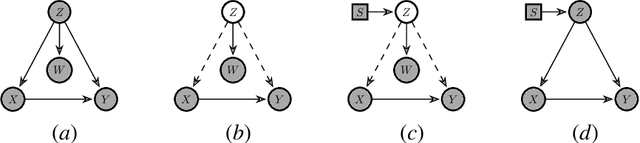
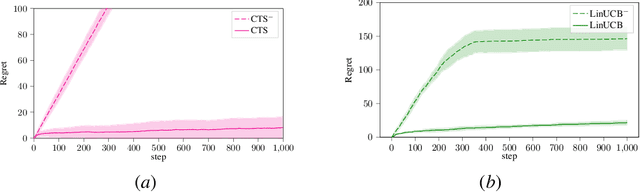
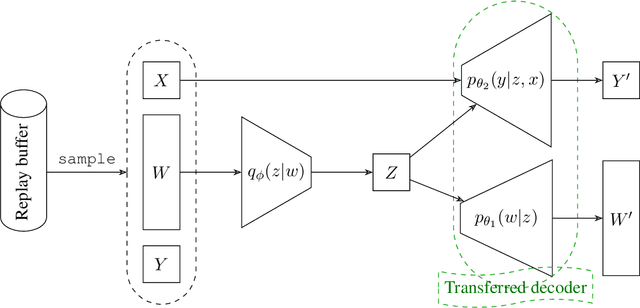
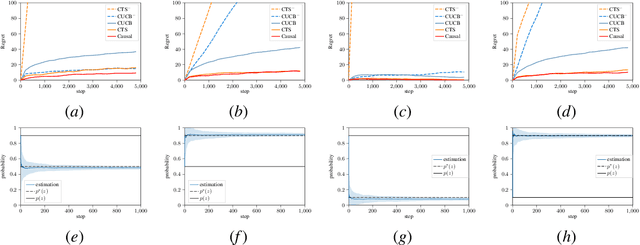
Transferring knowledge from one environment to another is an essential ability of intelligent systems. Nevertheless, when two environments are different, naively transferring all knowledge may deteriorate the performance, a phenomenon known as negative transfer. In this paper, we address this issue within the framework of multi-armed bandits from the perspective of causal inference. Specifically, we consider transfer learning in latent contextual bandits, where the actual context is hidden, but a potentially high-dimensional proxy is observable. We further consider a covariate shift in the context across environments. We show that naively transferring all knowledge for classical bandit algorithms in this setting led to negative transfer. We then leverage transportability theory from causal inference to develop algorithms that explicitly transfer effective knowledge for estimating the causal effects of interest in the target environment. Besides, we utilize variational autoencoders to approximate causal effects under the presence of a high-dimensional proxy. We test our algorithms on synthetic and semi-synthetic datasets, empirically demonstrating consistently improved learning efficiency across different proxies compared to baseline algorithms, showing the effectiveness of our causal framework in transferring knowledge.