Distributed Risk-Sensitive Safety Filters for Uncertain Discrete-Time Systems

Ensuring safety in multi-agent systems is a significant challenge, particularly in settings where centralized coordination is impractical. In this work, we propose a novel risk-sensitive safety filter for discrete-time multi-agent systems with uncertain dynamics that leverages control barrier functions (CBFs) defined through value functions. Our approach relies on centralized risk-sensitive safety conditions based on exponential risk operators to ensure robustness against model uncertainties. We introduce a distributed formulation of the safety filter by deriving two alternative strategies: one based on worst-case anticipation and another on proximity to a known safe policy. By allowing agents to switch between strategies, feasibility can be ensured. Through detailed numerical evaluations, we demonstrate the efficacy of our approach in maintaining safety without being overly conservative.

From Abstraction to Reality: DARPA's Vision for Robust Sim-to-Real Autonomy

The DARPA Transfer from Imprecise and Abstract Models to Autonomous Technologies (TIAMAT) program aims to address rapid and robust transfer of autonomy technologies across dynamic and complex environments, goals, and platforms. Existing methods for simulation-to-reality (sim-to-real) transfer often rely on high-fidelity simulations and struggle with broad adaptation, particularly in time-sensitive scenarios. Although many approaches have shown incredible performance at specific tasks, most techniques fall short when posed with unforeseen, complex, and dynamic real-world scenarios due to the inherent limitations of simulation. In contrast to current research that aims to bridge the gap between simulation environments and the real world through increasingly sophisticated simulations and a combination of methods typically assuming a small sim-to-real gap -- such as domain randomization, domain adaptation, imitation learning, meta-learning, policy distillation, and dynamic optimization -- TIAMAT takes a different approach by instead emphasizing transfer and adaptation of the autonomy stack directly to real-world environments by utilizing a breadth of low(er)-fidelity simulations to create broadly effective sim-to-real transfers. By abstractly learning from multiple simulation environments in reference to their shared semantics, TIAMAT's approaches aim to achieve abstract-to-real transfer for effective and rapid real-world adaptation. Furthermore, this program endeavors to improve the overall autonomy pipeline by addressing the inherent challenges in translating simulated behaviors into effective real-world performance.

Counterfactual Explanations for Model Ensembles Using Entropic Risk Measures

Counterfactual explanations indicate the smallest change in input that can translate to a different outcome for a machine learning model. Counterfactuals have generated immense interest in high-stakes applications such as finance, education, hiring, etc. In several use-cases, the decision-making process often relies on an ensemble of models rather than just one. Despite significant research on counterfactuals for one model, the problem of generating a single counterfactual explanation for an ensemble of models has received limited interest. Each individual model might lead to a different counterfactual, whereas trying to find a counterfactual accepted by all models might significantly increase cost (effort). We propose a novel strategy to find the counterfactual for an ensemble of models using the perspective of entropic risk measure. Entropic risk is a convex risk measure that satisfies several desirable properties. We incorporate our proposed risk measure into a novel constrained optimization to generate counterfactuals for ensembles that stay valid for several models. The main significance of our measure is that it provides a knob that allows for the generation of counterfactuals that stay valid under an adjustable fraction of the models. We also show that a limiting case of our entropic-risk-based strategy yields a counterfactual valid for all models in the ensemble (worst-case min-max approach). We study the trade-off between the cost (effort) for the counterfactual and its validity for an ensemble by varying degrees of risk aversion, as determined by our risk parameter knob. We validate our performance on real-world datasets.

Robust Stochastic Shortest-Path Planning via Risk-Sensitive Incremental Sampling

With the pervasiveness of Stochastic Shortest-Path (SSP) problems in high-risk industries, such as last-mile autonomous delivery and supply chain management, robust planning algorithms are crucial for ensuring successful task completion while mitigating hazardous outcomes. Mainstream chance-constrained incremental sampling techniques for solving SSP problems tend to be overly conservative and typically do not consider the likelihood of undesirable tail events. We propose an alternative risk-aware approach inspired by the asymptotically-optimal Rapidly-Exploring Random Trees (RRT*) planning algorithm, which selects nodes along path segments with minimal Conditional Value-at-Risk (CVaR). Our motivation rests on the step-wise coherence of the CVaR risk measure and the optimal substructure of the SSP problem. Thus, optimizing with respect to the CVaR at each sampling iteration necessarily leads to an optimal path in the limit of the sample size. We validate our approach via numerical path planning experiments in a two-dimensional grid world with obstacles and stochastic path-segment lengths. Our simulation results show that incorporating risk into the tree growth process yields paths with lengths that are significantly less sensitive to variations in the noise parameter, or equivalently, paths that are more robust to environmental uncertainty. Algorithmic analyses reveal similar query time and memory space complexity to the baseline RRT* procedure, with only a marginal increase in processing time. This increase is offset by significantly lower noise sensitivity and reduced planner failure rates.

Towards Efficient Risk-Sensitive Policy Gradient: An Iteration Complexity Analysis

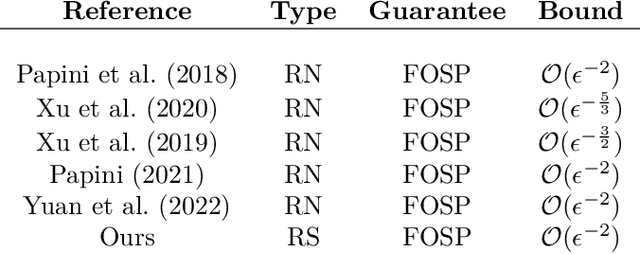
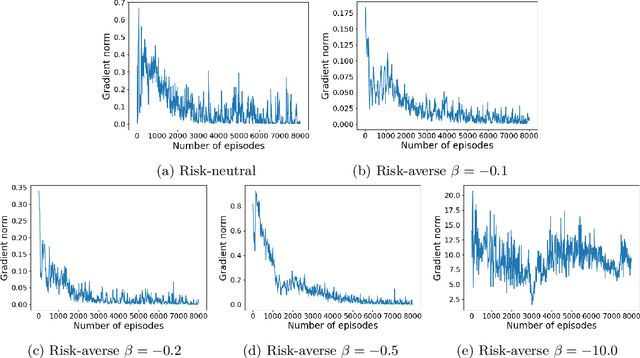
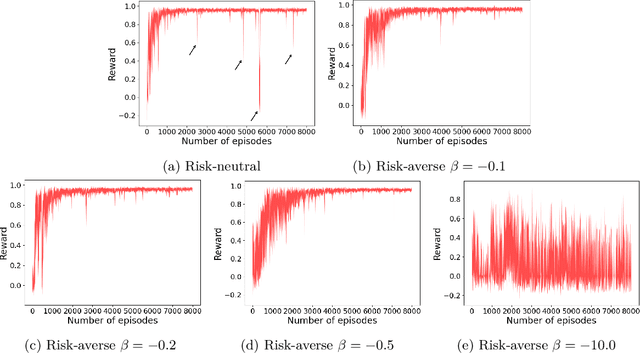
Reinforcement Learning (RL) has shown exceptional performance across various applications, enabling autonomous agents to learn optimal policies through interaction with their environments. However, traditional RL frameworks often face challenges in terms of iteration complexity and robustness. Risk-sensitive RL, which balances expected return and risk, has been explored for its potential to yield probabilistically robust policies, yet its iteration complexity analysis remains underexplored. In this study, we conduct a thorough iteration complexity analysis for the risk-sensitive policy gradient method, focusing on the REINFORCE algorithm and employing the exponential utility function. We obtain an iteration complexity of $\mathcal{O}(\epsilon^{-2})$ to reach an $\epsilon$-approximate first-order stationary point (FOSP). We investigate whether risk-sensitive algorithms can achieve better iteration complexity compared to their risk-neutral counterparts. Our theoretical analysis demonstrates that risk-sensitive REINFORCE can have a reduced number of iterations required for convergence. This leads to improved iteration complexity, as employing the exponential utility does not entail additional computation per iteration. We characterize the conditions under which risk-sensitive algorithms can achieve better iteration complexity. Our simulation results also validate that risk-averse cases can converge and stabilize more quickly after approximately half of the episodes compared to their risk-neutral counterparts.

Non-ergodicity in reinforcement learning: robustness via ergodicity transformations

Envisioned application areas for reinforcement learning (RL) include autonomous driving, precision agriculture, and finance, which all require RL agents to make decisions in the real world. A significant challenge hindering the adoption of RL methods in these domains is the non-robustness of conventional algorithms. In this paper, we argue that a fundamental issue contributing to this lack of robustness lies in the focus on the expected value of the return as the sole "correct" optimization objective. The expected value is the average over the statistical ensemble of infinitely many trajectories. For non-ergodic returns, this average differs from the average over a single but infinitely long trajectory. Consequently, optimizing the expected value can lead to policies that yield exceptionally high returns with probability zero but almost surely result in catastrophic outcomes. This problem can be circumvented by transforming the time series of collected returns into one with ergodic increments. This transformation enables learning robust policies by optimizing the long-term return for individual agents rather than the average across infinitely many trajectories. We propose an algorithm for learning ergodicity transformations from data and demonstrate its effectiveness in an instructive, non-ergodic environment and on standard RL benchmarks.

Robust Counterfactual Explanations for Neural Networks With Probabilistic Guarantees

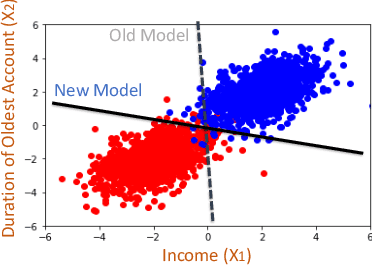
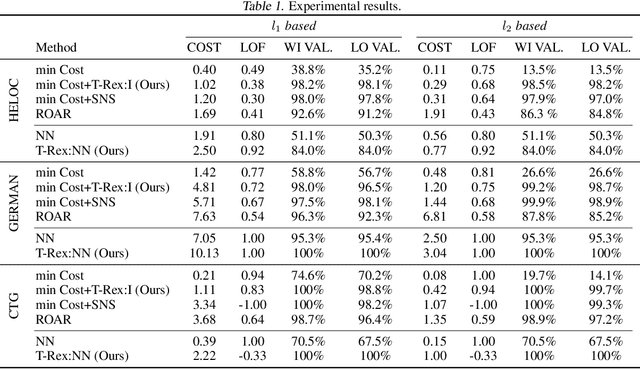
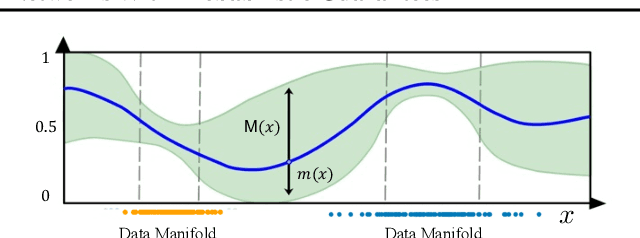
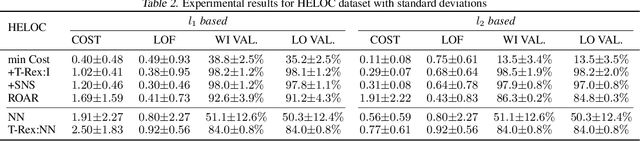
There is an emerging interest in generating robust counterfactual explanations that would remain valid if the model is updated or changed even slightly. Towards finding robust counterfactuals, existing literature often assumes that the original model $m$ and the new model $M$ are bounded in the parameter space, i.e., $\|\text{Params}(M){-}\text{Params}(m)\|{<}\Delta$. However, models can often change significantly in the parameter space with little to no change in their predictions or accuracy on the given dataset. In this work, we introduce a mathematical abstraction termed \emph{naturally-occurring} model change, which allows for arbitrary changes in the parameter space such that the change in predictions on points that lie on the data manifold is limited. Next, we propose a measure -- that we call \emph{Stability} -- to quantify the robustness of counterfactuals to potential model changes for differentiable models, e.g., neural networks. Our main contribution is to show that counterfactuals with sufficiently high value of \emph{Stability} as defined by our measure will remain valid after potential ``naturally-occurring'' model changes with high probability (leveraging concentration bounds for Lipschitz function of independent Gaussians). Since our quantification depends on the local Lipschitz constant around a data point which is not always available, we also examine practical relaxations of our proposed measure and demonstrate experimentally how they can be incorporated to find robust counterfactuals for neural networks that are close, realistic, and remain valid after potential model changes.

Risk-Sensitive Reinforcement Learning with Exponential Criteria

While risk-neutral reinforcement learning has shown experimental success in a number of applications, it is well-known to be non-robust with respect to noise and perturbations in the parameters of the system. For this reason, risk-sensitive reinforcement learning algorithms have been studied to introduce robustness and sample efficiency, and lead to better real-life performance. In this work, we introduce new model-free risk-sensitive reinforcement learning algorithms as variations of widely-used Policy Gradient algorithms with similar implementation properties. In particular, we study the effect of exponential criteria on the risk-sensitivity of the policy of a reinforcement learning agent, and develop variants of the Monte Carlo Policy Gradient algorithm and the online (temporal-difference) Actor-Critic algorithm. Analytical results showcase that the use of exponential criteria generalize commonly used ad-hoc regularization approaches. The implementation, performance, and robustness properties of the proposed methods are evaluated in simulated experiments.