Private Counterfactual Retrieval With Immutable Features

In a classification task, counterfactual explanations provide the minimum change needed for an input to be classified into a favorable class. We consider the problem of privately retrieving the exact closest counterfactual from a database of accepted samples while enforcing that certain features of the input sample cannot be changed, i.e., they are \emph{immutable}. An applicant (user) whose feature vector is rejected by a machine learning model wants to retrieve the sample closest to them in the database without altering a private subset of their features, which constitutes the immutable set. While doing this, the user should keep their feature vector, immutable set and the resulting counterfactual index information-theoretically private from the institution. We refer to this as immutable private counterfactual retrieval (I-PCR) problem which generalizes PCR to a more practical setting. In this paper, we propose two I-PCR schemes by leveraging techniques from private information retrieval (PIR) and characterize their communication costs. Further, we quantify the information that the user learns about the database and compare it for the proposed schemes.

Quantifying Knowledge Distillation Using Partial Information Decomposition

Knowledge distillation provides an effective method for deploying complex machine learning models in resource-constrained environments. It typically involves training a smaller student model to emulate either the probabilistic outputs or the internal feature representations of a larger teacher model. By doing so, the student model often achieves substantially better performance on a downstream task compared to when it is trained independently. Nevertheless, the teacher's internal representations can also encode noise or additional information that may not be relevant to the downstream task. This observation motivates our primary question: What are the information-theoretic limits of knowledge transfer? To this end, we leverage a body of work in information theory called Partial Information Decomposition (PID) to quantify the distillable and distilled knowledge of a teacher's representation corresponding to a given student and a downstream task. Moreover, we demonstrate that this metric can be practically used in distillation to address challenges caused by the complexity gap between the teacher and the student representations.

Private Counterfactual Retrieval

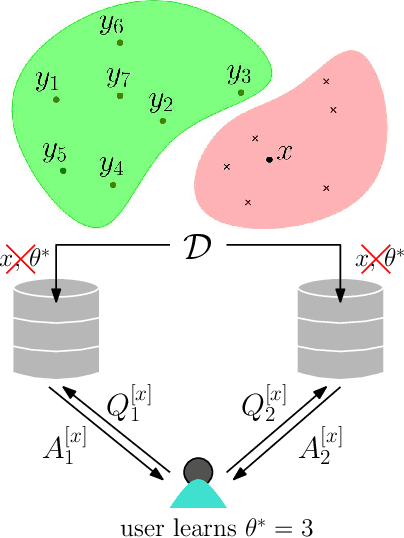
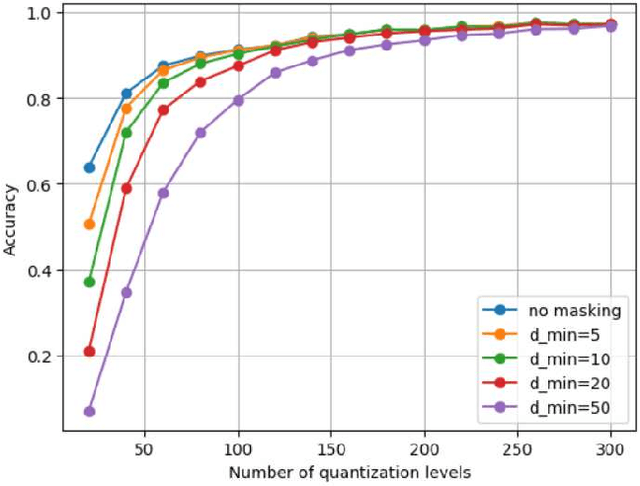
Transparency and explainability are two extremely important aspects to be considered when employing black-box machine learning models in high-stake applications. Providing counterfactual explanations is one way of catering this requirement. However, this also poses a threat to the privacy of both the institution that is providing the explanation as well as the user who is requesting it. In this work, we propose multiple schemes inspired by private information retrieval (PIR) techniques which ensure the \emph{user's privacy} when retrieving counterfactual explanations. We present a scheme which retrieves the \emph{exact} nearest neighbor counterfactual explanation from a database of accepted points while achieving perfect (information-theoretic) privacy for the user. While the scheme achieves perfect privacy for the user, some leakage on the database is inevitable which we quantify using a mutual information based metric. Furthermore, we propose strategies to reduce this leakage to achieve an advanced degree of database privacy. We extend these schemes to incorporate user's preference on transforming their attributes, so that a more actionable explanation can be received. Since our schemes rely on finite field arithmetic, we empirically validate our schemes on real datasets to understand the trade-off between the accuracy and the finite field sizes.

Quantifying Prediction Consistency Under Model Multiplicity in Tabular LLMs

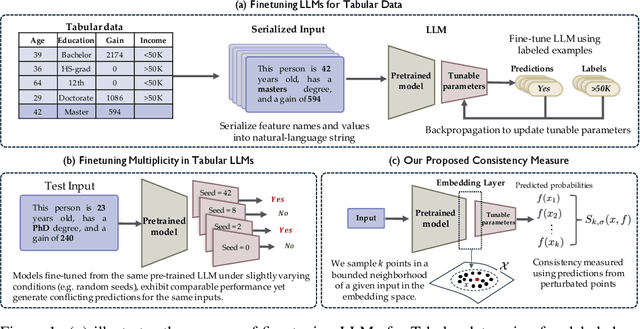
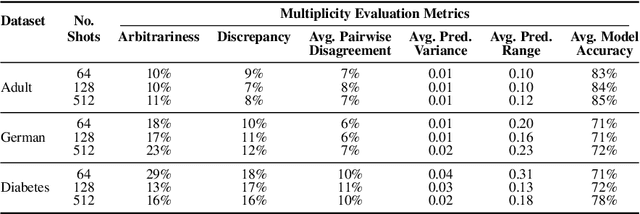
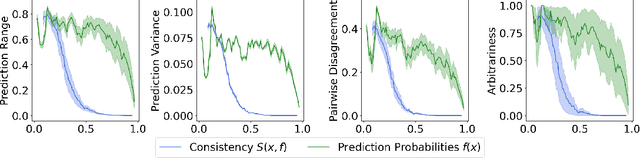
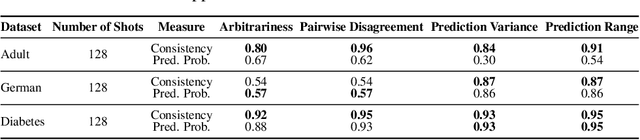
Fine-tuning large language models (LLMs) on limited tabular data for classification tasks can lead to \textit{fine-tuning multiplicity}, where equally well-performing models make conflicting predictions on the same inputs due to variations in the training process (i.e., seed, random weight initialization, retraining on additional or deleted samples). This raises critical concerns about the robustness and reliability of Tabular LLMs, particularly when deployed for high-stakes decision-making, such as finance, hiring, education, healthcare, etc. This work formalizes the challenge of fine-tuning multiplicity in Tabular LLMs and proposes a novel metric to quantify the robustness of individual predictions without expensive model retraining. Our metric quantifies a prediction's stability by analyzing (sampling) the model's local behavior around the input in the embedding space. Interestingly, we show that sampling in the local neighborhood can be leveraged to provide probabilistic robustness guarantees against a broad class of fine-tuned models. By leveraging Bernstein's Inequality, we show that predictions with sufficiently high robustness (as defined by our measure) will remain consistent with high probability. We also provide empirical evaluation on real-world datasets to support our theoretical results. Our work highlights the importance of addressing fine-tuning instabilities to enable trustworthy deployment of LLMs in high-stakes and safety-critical applications.

Quantifying Spuriousness of Biased Datasets Using Partial Information Decomposition

Spurious patterns refer to a mathematical association between two or more variables in a dataset that are not causally related. However, this notion of spuriousness, which is usually introduced due to sampling biases in the dataset, has classically lacked a formal definition. To address this gap, this work presents the first information-theoretic formalization of spuriousness in a dataset (given a split of spurious and core features) using a mathematical framework called Partial Information Decomposition (PID). Specifically, we disentangle the joint information content that the spurious and core features share about another target variable (e.g., the prediction label) into distinct components, namely unique, redundant, and synergistic information. We propose the use of unique information, with roots in Blackwell Sufficiency, as a novel metric to formally quantify dataset spuriousness and derive its desirable properties. We empirically demonstrate how higher unique information in the spurious features in a dataset could lead a model into choosing the spurious features over the core features for inference, often having low worst-group-accuracy. We also propose a novel autoencoder-based estimator for computing unique information that is able to handle high-dimensional image data. Finally, we also show how this unique information in the spurious feature is reduced across several dataset-based spurious-pattern-mitigation techniques such as data reweighting and varying levels of background mixing, demonstrating a novel tradeoff between unique information (spuriousness) and worst-group-accuracy.

Model Reconstruction Using Counterfactual Explanations: Mitigating the Decision Boundary Shift

Counterfactual explanations find ways of achieving a favorable model outcome with minimum input perturbation. However, counterfactual explanations can also be exploited to steal the model by strategically training a surrogate model to give similar predictions as the original (target) model. In this work, we investigate model extraction by specifically leveraging the fact that the counterfactual explanations also lie quite close to the decision boundary. We propose a novel strategy for model extraction that we call Counterfactual Clamping Attack (CCA) which trains a surrogate model using a unique loss function that treats counterfactuals differently than ordinary instances. Our approach also alleviates the related problem of decision boundary shift that arises in existing model extraction attacks which treat counterfactuals as ordinary instances. We also derive novel mathematical relationships between the error in model approximation and the number of queries using polytope theory. Experimental results demonstrate that our strategy provides improved fidelity between the target and surrogate model predictions on several real world datasets.

Distribution of the Scaled Condition Number of Single-spiked Complex Wishart Matrices

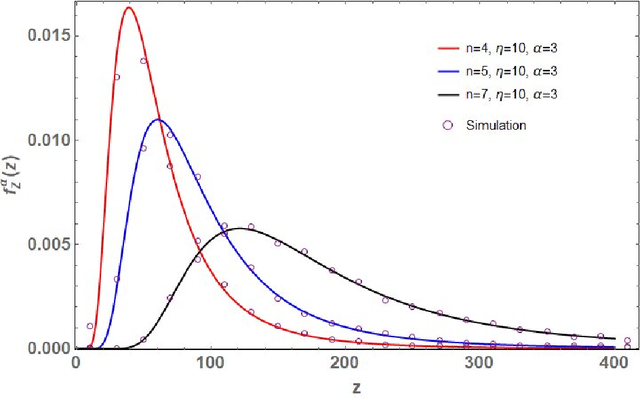
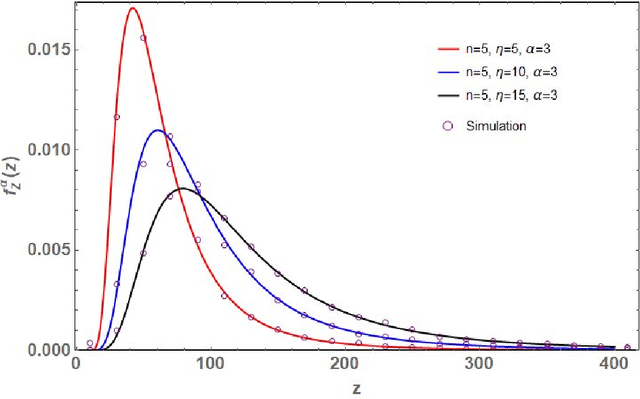
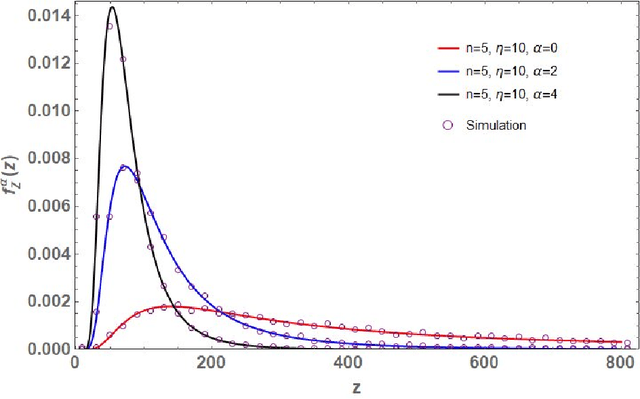
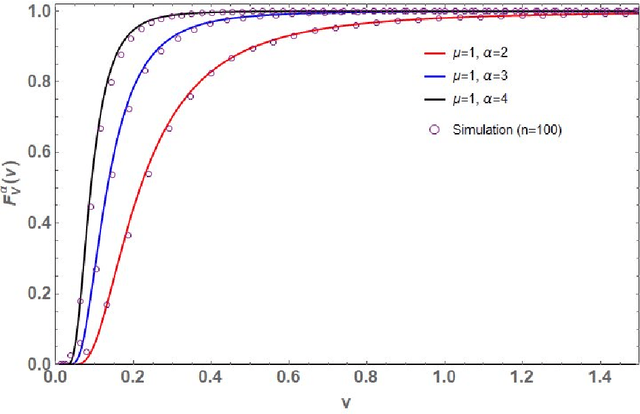
Let $\mathbf{X}\in\mathbb{C}^{m\times n}$ ($m\geq n$) be a random matrix with independent rows each distributed as complex multivariate Gaussian with zero mean and {\it single-spiked} covariance matrix $\mathbf{I}_n+ \eta \mathbf{u}\mathbf{u}^*$, where $\mathbf{I}_n$ is the $n\times n$ identity matrix, $\mathbf{u}\in\mathbb{C}^{n\times n}$ is an arbitrary vector with a unit Euclidean norm, $\eta\geq 0$ is a non-random parameter, and $(\cdot)^*$ represents conjugate-transpose. This paper investigates the distribution of the random quantity $\kappa_{\text{SC}}^2(\mathbf{X})=\sum_{k=1}^n \lambda_k/\lambda_1$, where $0<\lambda_1<\lambda_2<\ldots<\lambda_n<\infty$ are the ordered eigenvalues of $\mathbf{X}^*\mathbf{X}$ (i.e., single-spiked Wishart matrix). This random quantity is intimately related to the so called {\it scaled condition number} or the Demmel condition number (i.e., $\kappa_{\text{SC}}(\mathbf{X})$) and the minimum eigenvalue of the fixed trace Wishart-Laguerre ensemble (i.e., $\kappa_{\text{SC}}^{-2}(\mathbf{X})$). In particular, we use an orthogonal polynomial approach to derive an exact expression for the probability density function of $\kappa_{\text{SC}}^2(\mathbf{X})$ which is amenable to asymptotic analysis as matrix dimensions grow large. Our asymptotic results reveal that, as $m,n\to\infty$ such that $m-n$ is fixed and when $\eta$ scales on the order of $1/n$, $\kappa_{\text{SC}}^2(\mathbf{X})$ scales on the order of $n^3$. In this respect we establish simple closed-form expressions for the limiting distributions.