Distribution of the Scaled Condition Number of Single-spiked Complex Wishart Matrices
Paper and Code
May 11, 2021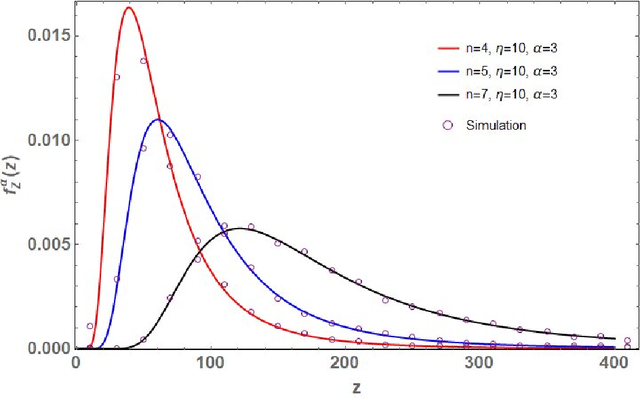
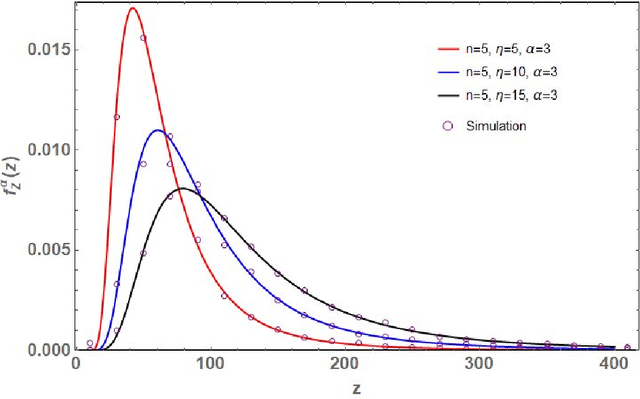
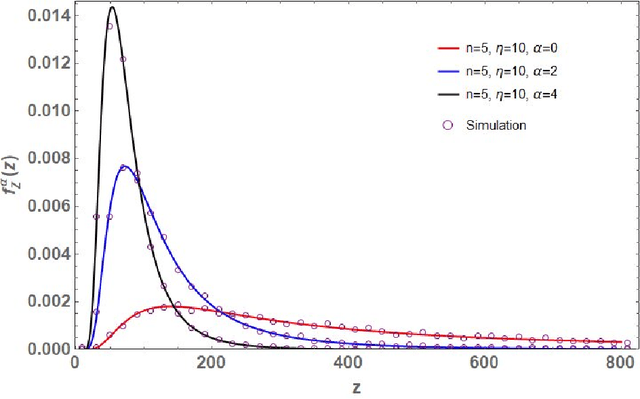
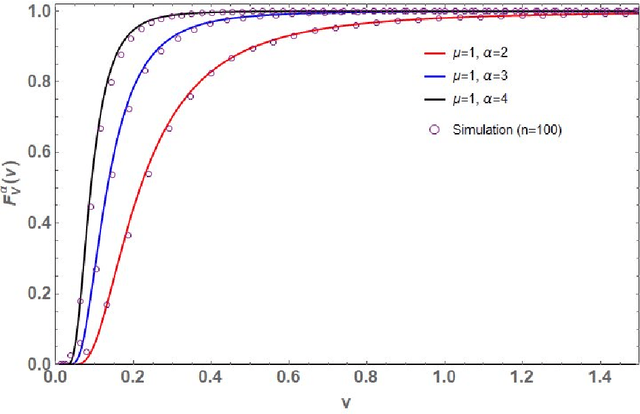
Let $\mathbf{X}\in\mathbb{C}^{m\times n}$ ($m\geq n$) be a random matrix with independent rows each distributed as complex multivariate Gaussian with zero mean and {\it single-spiked} covariance matrix $\mathbf{I}_n+ \eta \mathbf{u}\mathbf{u}^*$, where $\mathbf{I}_n$ is the $n\times n$ identity matrix, $\mathbf{u}\in\mathbb{C}^{n\times n}$ is an arbitrary vector with a unit Euclidean norm, $\eta\geq 0$ is a non-random parameter, and $(\cdot)^*$ represents conjugate-transpose. This paper investigates the distribution of the random quantity $\kappa_{\text{SC}}^2(\mathbf{X})=\sum_{k=1}^n \lambda_k/\lambda_1$, where $0<\lambda_1<\lambda_2<\ldots<\lambda_n<\infty$ are the ordered eigenvalues of $\mathbf{X}^*\mathbf{X}$ (i.e., single-spiked Wishart matrix). This random quantity is intimately related to the so called {\it scaled condition number} or the Demmel condition number (i.e., $\kappa_{\text{SC}}(\mathbf{X})$) and the minimum eigenvalue of the fixed trace Wishart-Laguerre ensemble (i.e., $\kappa_{\text{SC}}^{-2}(\mathbf{X})$). In particular, we use an orthogonal polynomial approach to derive an exact expression for the probability density function of $\kappa_{\text{SC}}^2(\mathbf{X})$ which is amenable to asymptotic analysis as matrix dimensions grow large. Our asymptotic results reveal that, as $m,n\to\infty$ such that $m-n$ is fixed and when $\eta$ scales on the order of $1/n$, $\kappa_{\text{SC}}^2(\mathbf{X})$ scales on the order of $n^3$. In this respect we establish simple closed-form expressions for the limiting distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge