Performance Analysis for Multi-User Holographic MIMO Downlink with Matched Filter Precoding

Holographic MIMO (HMIMO) has emerged as a promising solution for future wireless systems by enabling ultra-dense, spatially continuous antenna deployments. While prior studies have primarily focused on electromagnetic (EM) modeling or simulation-based performance analysis, a rigorous communication-theoretic framework remains largely unexplored. This paper presents the first analytical performance study of a multi-user HMIMO downlink system with matched filter (MF) precoding - a low-complexity baseline scheme. By incorporating multipath propagation, mutual coupling, and element excitation, we derive a novel closed-form expression for the MF signal-to-interference-plus-noise ratio (SINR) using an equivalent random variable model. Leveraging bivariate gamma distributions, we then develop tractable throughput approximations under full, partial, and no channel state information (CSI) scenarios. Additionally, we formulate a max-min beamforming problem to benchmark optimal user fairness performance. Numerical results validate the accuracy of the proposed framework and reveal that MF precoding achieves competitive performance with strong robustness to low SINR and CSI uncertainty.

Localization-Based Beam Focusing in Near-Field Communications

Shifting 6G-and-beyond wireless communication systems to higher frequency bands and the utilization of massive multiple-input multiple-output arrays will extend the near-field region, affecting beamforming and user localization schemes. In this paper, we propose a localization-based beam-focusing strategy that leverages the dominant line-of-sight (LoS) propagation arising at mmWave and sub-THz frequencies. To support this approach, we analyze the 2D-MUSIC algorithm for distance estimation by examining its spectrum in simplified, tractable setups with minimal numbers of antennas and users. Lastly, we compare the proposed localization-based beam focusing, with locations estimated via 2D-MUSIC, with zero forcing with pilot-based channel estimation in terms of uplink sum spectral efficiency. Our numerical results show that the proposed method becomes more effective under LoS-dominated propagation, short coherence blocks, and strong noise power arising at high carrier frequencies and with large bandwidths.

Eigenvalue-Based Detection in MIMO Systems for Integrated Sensing and Communication

This paper considers a MIMO Integrated Sensing and Communication (ISAC) system, where a base station simultaneously serves a MIMO communication user and a remote MIMO sensing receiver, without channel state information (CSI) at the transmitter. Existing MIMO ISAC literature often prioritizes communication rate or detection probability, typically under constant false-alarm rate (CFAR) assumptions, without jointly analyzing detection reliability and communication constraints. To address this gap, we adopt an eigenvalue-based detector for robust sensing and use a performance metric, the total detection error, that jointly captures false-alarm and missed-detection probabilities. We derive novel closed-form expressions for both probabilities under the eigenvalue detector, enabling rigorous sensing analysis. Using these expressions, we formulate and solve a joint power allocation and threshold optimization problem that minimizes total detection error while meeting a minimum communication rate requirement. Simulation results demonstrate that the proposed joint design substantially outperforms conventional CFAR-based schemes, highlighting the benefits of power- and threshold-aware optimization in MIMO ISAC systems.

Max-Min Fairness for Stacked Intelligent Metasurface-Assisted Multi-User MISO Systems

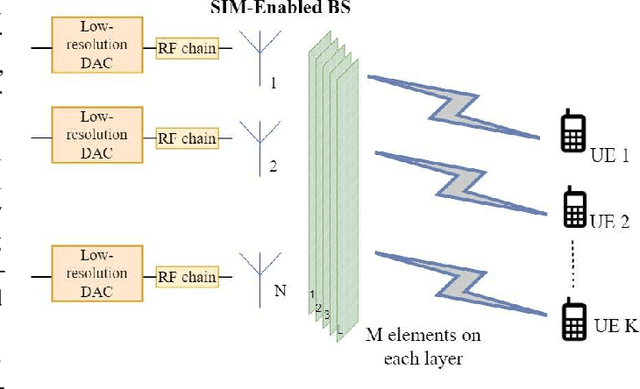
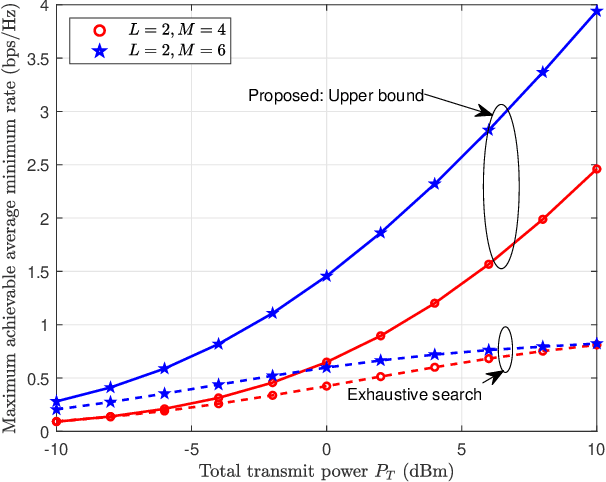
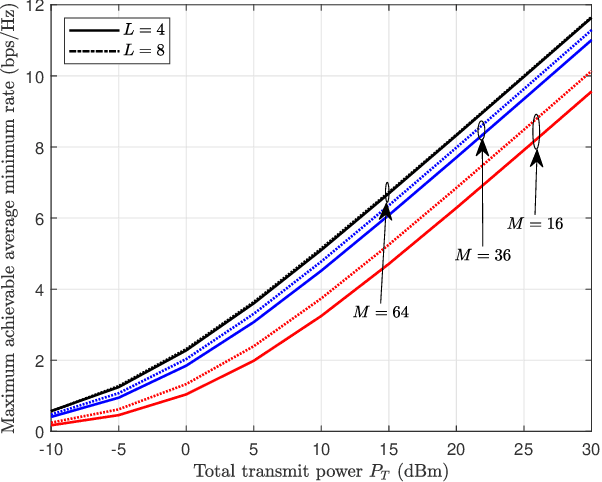
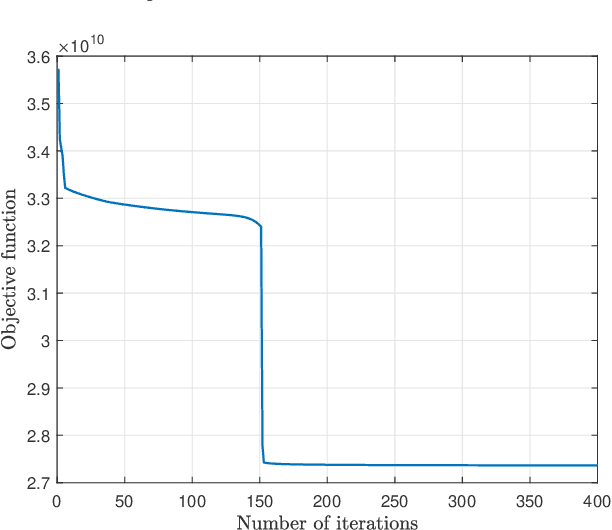
Stacked intelligent metasurface (SIM) is an emerging technology that uses multiple reconfigurable surface layers to enable flexible wave-based beamforming. In this paper, we focus on an \ac{SIM}-assisted multi-user multiple-input single-output system, where it is essential to ensure that all users receive a fair and reliable service level. To this end, we develop two max-min fairness algorithms based on instantaneous channel state information (CSI) and statistical CSI. For the instantaneous CSI case, we propose an alternating optimization algorithm that jointly optimizes power allocation using geometric programming and wave-based beamforming coefficients using the gradient descent-ascent method. For the statistical CSI case, since deriving an exact expression for the average minimum achievable rate is analytically intractable, we derive a tight upper bound and thereby formulate a stochastic optimization problem. This problem is then solved, capitalizing on an alternating approach combining geometric programming and gradient descent algorithms, to obtain the optimal policies. Our numerical results show significant improvements in the minimum achievable rate compared to the benchmark schemes. In particular, for the instantaneous CSI scenario, the individual impact of the optimal wave-based beamforming is significantly higher than that of the power allocation strategy. Moreover, the proposed upper bound is shown to be tight in the low signal-to-noise ratio regime under the statistical CSI.

Uniform Planar Array Based Weighted Cooperative Spectrum Sensing for Cognitive Radio Networks

Cooperative spectrum sensing (CSS) is essential for improving the spectrum efficiency and reliability of cognitive radio applications. Next-generation wireless communication networks increasingly employ uniform planar arrays (UPA) due to their ability to steer beamformers towards desired directions, mitigating interference and eavesdropping. However, the application of UPA-based CSS in cognitive radio remains largely unexplored. This paper proposes a multi-beam UPA-based weighted CSS (WCSS) framework to enhance detection reliability, applicable to various cognitive radio networks, including cellular, vehicular, and satellite communications. We first propose a weighting factor for commonly used energy detection (ED) and eigenvalue detection (EVD) techniques, based on the spatial variation of signal strengths resulting from UPA antenna beamforming. We then analytically characterize the performance of both weighted ED and weighted EVD by deriving closed-form expressions for false alarm and detection probabilities. Our numerical results, considering both static and dynamic user behaviors, demonstrate the superiority of WCSS in enhancing sensing performance compared to uniformly weighted detectors.

Detection of Signals in Colored Noise: Roy's Largest Root Test for Non-central $F$-matrices

This paper investigates the signal detection problem in colored noise with an unknown covariance matrix. In particular, we focus on detecting a non-random signal by capitalizing on the leading eigenvalue (a.k.a. Roy's largest root) of the whitened sample covariance matrix as the test statistic. To this end, the whitened sample covariance matrix is constructed via \(m\)-dimensional \(p \) plausible signal-bearing samples and \(m\)-dimensional \(n \) noise-only samples. Since the signal is non-random, the whitened sample covariance matrix turns out to have a {\it non-central} \(F\)-distribution with a rank-one non-centrality parameter. Therefore, the performance of the test entails the statistical characterization of the leading eigenvalue of the non-central \(F\)-matrix, which we address by deriving its cumulative distribution function (c.d.f.) in closed-form by leveraging the powerful orthogonal polynomial approach in random matrix theory. This new c.d.f. has been instrumental in analyzing the receiver operating characteristic (ROC) of the detector. We also extend our analysis into the high dimensional regime in which \(m,n\), and \(p\) diverge such that \(m/n\) and \(m/p\) remain fixed. It turns out that, when \(m=n\) and fixed, the power of the test improves if the signal-to-noise ratio (SNR) is of at least \(O(p)\), whereas the corresponding SNR in the high dimensional regime is of at least \(O(p^2)\). Nevertheless, more intriguingly, for \(m<n\) with the SNR of order \(O(p)\), the leading eigenvalue does not have power to detect {\it weak} signals in the high dimensional regime.

Signal Detection in Colored Noise Using the Condition Number of $F$-Matrices

Signal detection in colored noise with an unknown covariance matrix has numerous applications across various scientific and engineering disciplines. The analysis focuses on the square of the condition number \(\kappa^2(\cdot)\), defined as the ratio of the largest to smallest eigenvalue \((\lambda_{\text{max}}/\lambda_{\text{min}})\) of the whitened sample covariance matrix \(\bm{\widehat{\Psi}}\), constructed from \(p\) signal-plus-noise samples and \(n\) noise-only samples, both \(m\)-dimensional. This statistic is denoted as \(\kappa^2(\bm{\widehat{\Psi}})\). A finite-dimensional characterization of the false alarm probability for this statistic under the null and alternative hypotheses has been an open problem. Therefore, in this work, we address this by deriving the cumulative distribution function (c.d.f.) of \(\kappa^2(\bm{\widehat{\Psi}})\) using the powerful orthogonal polynomial approach in random matrix theory. These c.d.f. expressions have been used to statistically characterize the performance of \(\kappa^2(\bm{\widehat{\Psi}})\).

Detection of Signals in Colored Noise: Leading Eigenvalue Test for Non-central $F$-matrices

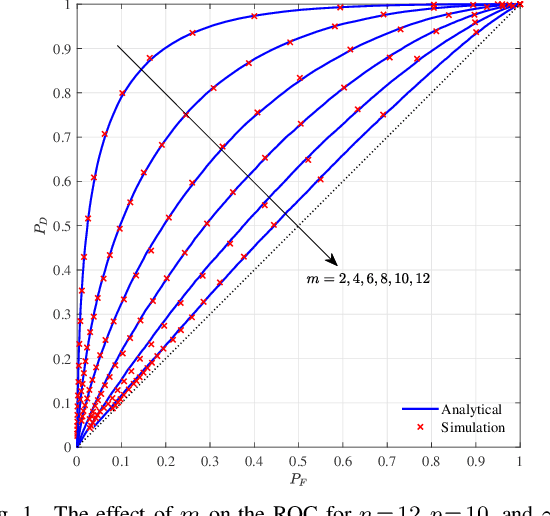
This paper investigates the signal detection problem in colored noise with an unknown covariance matrix. In particular, we focus on detecting an unknown non-random signal by capitalizing on the leading eigenvalue of the whitened sample covariance matrix as the test statistic (a.k.a. Roy's largest root test). Since the unknown signal is non-random, the whitened sample covariance matrix turns out to have a non-central $F$-distribution. This distribution assumes a singular or non-singular form depending on whether the number of observations $p\lessgtr$ the system dimensionality $m$. Therefore, we statistically characterize the leading eigenvalue of the singular and non-singular $F$-matrices by deriving their cumulative distribution functions (c.d.f.). Subsequently, they have been utilized in deriving the corresponding receiver operating characteristic (ROC) profiles. We also extend our analysis into the high dimensional domain. It turns out that, when the signal is sufficiently strong, the maximum eigenvalue can reliably detect it in this regime. Nevertheless, weak signals cannot be detected in the high dimensional regime with the leading eigenvalue.

Generalized Eigenvalue Based Detection of Signals in Colored Noise: A Sample Deficient Analysis

This paper investigates the signal detection problem in colored noise with an unknown covariance matrix. To be specific, we consider a scenario in which the number of signal bearing samples ($n$) is strictly smaller than the dimensionality of the signal space ($m$). Our test statistic is the leading generalized eigenvalue of the whitened sample covariance matrix (a.k.a. $F$-matrix) which is constructed by whitening the signal bearing sample covariance matrix with noise-only sample covariance matrix. The sample deficiency (i.e., $m>n$) in turn makes this $F$-matrix rank deficient, thereby singular. Therefore, an exact statistical characterization of the leading generalized eigenvalue (l.g.e.) of a singular $F$-matrix is of paramount importance to assess the performance of the detector (i.e., the receiver operating characteristics (ROC)). To this end, we employ the powerful orthogonal polynomial approach to derive a new finite dimensional c.d.f. expression for the l.g.e. of a singular $F$-matrix. It turns out that when the noise only sample covariance matrix is nearly rank deficient and the signal-to-noise ratio is $O(m)$, the ROC profile converges to a limit.

Flex-Net: A Graph Neural Network Approach to Resource Management in Flexible Duplex Networks

Flexible duplex networks allow users to dynamically employ uplink and downlink channels without static time scheduling, thereby utilizing the network resources efficiently. This work investigates the sum-rate maximization of flexible duplex networks. In particular, we consider a network with pairwise-fixed communication links. Corresponding combinatorial optimization is a non-deterministic polynomial (NP)-hard without a closed-form solution. In this respect, the existing heuristics entail high computational complexity, raising a scalability issue in large networks. Motivated by the recent success of Graph Neural Networks (GNNs) in solving NP-hard wireless resource management problems, we propose a novel GNN architecture, named Flex-Net, to jointly optimize the communication direction and transmission power. The proposed GNN produces near-optimal performance meanwhile maintaining a low computational complexity compared to the most commonly used techniques. Furthermore, our numerical results shed light on the advantages of using GNNs in terms of sample complexity, scalability, and generalization capability.