On the Convergence of Inexact Gradient Descent with Controlled Synchronization Steps
Paper and Code
Aug 16, 2022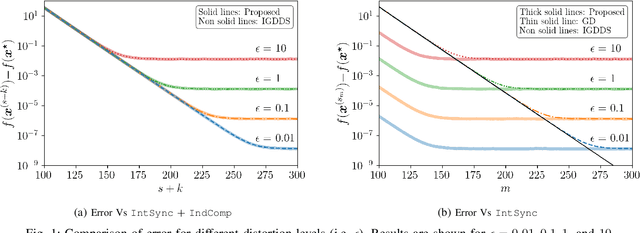
We develop a gradient-like algorithm to minimize a sum of peer objective functions based on coordination through a peer interconnection network. The coordination admits two stages: the first is to constitute a gradient, possibly with errors, for updating locally replicated decision variables at each peer and the second is used for error-free averaging for synchronizing local replicas. Unlike many related algorithms, the errors permitted in our algorithm can cover a wide range of inexactnesses, as long as they are bounded. Moreover, the second stage is not conducted in a periodic manner, like many related algorithms. Instead, a locally verifiable criterion is devised to dynamically trigger the peer-to-peer coordination at the second stage, so that expensive communication overhead for error-free averaging can significantly be reduced. Finally, the convergence of the algorithm is established under mild conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge