Opportunistic Beamforming and Dynamic Scheduling for Multi-User MIMO-ISAC Systems

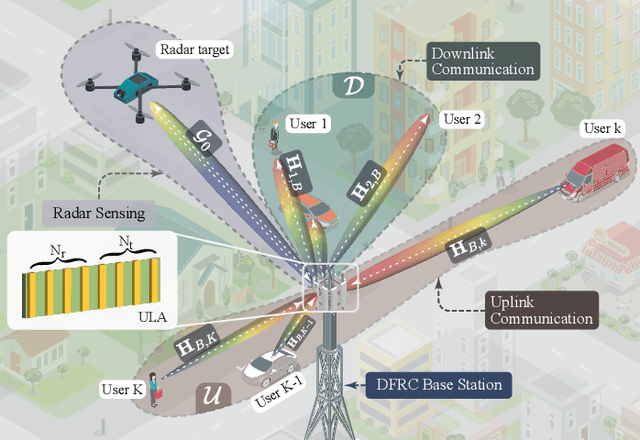
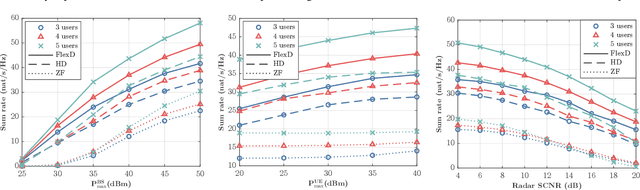
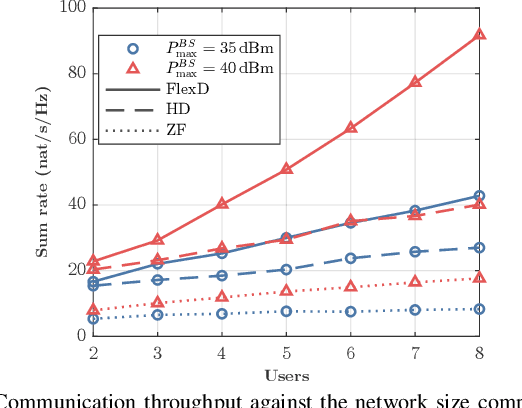
This research presents a novel framework integrating Flexible-Duplex (FlexD) and Integrated Sensing and Communications (ISAC) technologies to address the challenges of spectrum efficiency and resource optimization in next-generation wireless networks. We develop a unified system model for a dual-functional radar-communication base station with multiple-input multiple-output capabilities, enabling dynamic uplink and downlink channel allocation. The framework maximizes network throughput while maintaining radar sensing performance, subject to signal-to-clutter-plus-noise ratio (SCNR) requirements and power constraints. Given the non-convex and combinatorial nature of the resulting optimization problem, we propose an iterative algorithm that converges to a locally optimal solution. Extensive simulations demonstrate the superiority of the proposed FlexD-ISAC framework compared to conventional half-duplex networks. Additionally, sensitivity analyses reveal the impact of SCNR requirements and power constraints on system performance, providing valuable insights for practical implementation. This work establishes a foundation for future research in dynamic, resource-efficient wireless systems that simultaneously support sensing and communication capabilities.

Graph Neural Networks for Physical-Layer Security in Multi-User Flexible-Duplex Networks

This paper explores Physical-Layer Security (PLS) in Flexible Duplex (FlexD) networks, considering scenarios involving eavesdroppers. Our investigation revolves around the intricacies of the sum secrecy rate maximization problem, particularly when faced with coordinated and distributed eavesdroppers employing a Minimum Mean Square Error (MMSE) receiver. Our contributions include an iterative classical optimization solution and an unsupervised learning strategy based on Graph Neural Networks (GNNs). To the best of our knowledge, this work marks the initial exploration of GNNs for PLS applications. Additionally, we extend the GNN approach to address the absence of eavesdroppers' channel knowledge. Extensive numerical simulations highlight FlexD's superiority over Half-Duplex (HD) communications and the GNN approach's superiority over the classical method in both performance and time complexity.

Flex-Net: A Graph Neural Network Approach to Resource Management in Flexible Duplex Networks

Flexible duplex networks allow users to dynamically employ uplink and downlink channels without static time scheduling, thereby utilizing the network resources efficiently. This work investigates the sum-rate maximization of flexible duplex networks. In particular, we consider a network with pairwise-fixed communication links. Corresponding combinatorial optimization is a non-deterministic polynomial (NP)-hard without a closed-form solution. In this respect, the existing heuristics entail high computational complexity, raising a scalability issue in large networks. Motivated by the recent success of Graph Neural Networks (GNNs) in solving NP-hard wireless resource management problems, we propose a novel GNN architecture, named Flex-Net, to jointly optimize the communication direction and transmission power. The proposed GNN produces near-optimal performance meanwhile maintaining a low computational complexity compared to the most commonly used techniques. Furthermore, our numerical results shed light on the advantages of using GNNs in terms of sample complexity, scalability, and generalization capability.