Graph Neural Networks for Resource Allocation in Multi-Channel Wireless Networks

As the number of mobile devices continues to grow, interference has become a major bottleneck in improving data rates in wireless networks. Efficient joint channel and power allocation (JCPA) is crucial for managing interference. In this paper, we first propose an enhanced WMMSE (eWMMSE) algorithm to solve the JCPA problem in multi-channel wireless networks. To reduce the computational complexity of iterative optimization, we further introduce JCPGNN-M, a graph neural network-based solution that enables simultaneous multi-channel allocation for each user. We reformulate the problem as a Lagrangian function, which allows us to enforce the total power constraints systematically. Our solution involves combining this Lagrangian framework with GNNs and iteratively updating the Lagrange multipliers and resource allocation scheme. Unlike existing GNN-based methods that limit each user to a single channel, JCPGNN-M supports efficient spectrum reuse and scales well in dense network scenarios. Simulation results show that JCPGNN-M achieves better data rate compared to eWMMSE. Meanwhile, the inference time of JCPGNN-M is much lower than eWMMS, and it can generalize well to larger networks.

Opportunistic Beamforming and Dynamic Scheduling for Multi-User MIMO-ISAC Systems

This research presents a novel framework integrating Flexible-Duplex (FlexD) and Integrated Sensing and Communications (ISAC) technologies to address the challenges of spectrum efficiency and resource optimization in next-generation wireless networks. We develop a unified system model for a dual-functional radar-communication base station with multiple-input multiple-output capabilities, enabling dynamic uplink and downlink channel allocation. The framework maximizes network throughput while maintaining radar sensing performance, subject to signal-to-clutter-plus-noise ratio (SCNR) requirements and power constraints. Given the non-convex and combinatorial nature of the resulting optimization problem, we propose an iterative algorithm that converges to a locally optimal solution. Extensive simulations demonstrate the superiority of the proposed FlexD-ISAC framework compared to conventional half-duplex networks. Additionally, sensitivity analyses reveal the impact of SCNR requirements and power constraints on system performance, providing valuable insights for practical implementation. This work establishes a foundation for future research in dynamic, resource-efficient wireless systems that simultaneously support sensing and communication capabilities.

Detection of Signals in Colored Noise: Roy's Largest Root Test for Non-central $F$-matrices

This paper investigates the signal detection problem in colored noise with an unknown covariance matrix. In particular, we focus on detecting a non-random signal by capitalizing on the leading eigenvalue (a.k.a. Roy's largest root) of the whitened sample covariance matrix as the test statistic. To this end, the whitened sample covariance matrix is constructed via \(m\)-dimensional \(p \) plausible signal-bearing samples and \(m\)-dimensional \(n \) noise-only samples. Since the signal is non-random, the whitened sample covariance matrix turns out to have a {\it non-central} \(F\)-distribution with a rank-one non-centrality parameter. Therefore, the performance of the test entails the statistical characterization of the leading eigenvalue of the non-central \(F\)-matrix, which we address by deriving its cumulative distribution function (c.d.f.) in closed-form by leveraging the powerful orthogonal polynomial approach in random matrix theory. This new c.d.f. has been instrumental in analyzing the receiver operating characteristic (ROC) of the detector. We also extend our analysis into the high dimensional regime in which \(m,n\), and \(p\) diverge such that \(m/n\) and \(m/p\) remain fixed. It turns out that, when \(m=n\) and fixed, the power of the test improves if the signal-to-noise ratio (SNR) is of at least \(O(p)\), whereas the corresponding SNR in the high dimensional regime is of at least \(O(p^2)\). Nevertheless, more intriguingly, for \(m<n\) with the SNR of order \(O(p)\), the leading eigenvalue does not have power to detect {\it weak} signals in the high dimensional regime.

GNN-Based Joint Channel and Power Allocation in Heterogeneous Wireless Networks

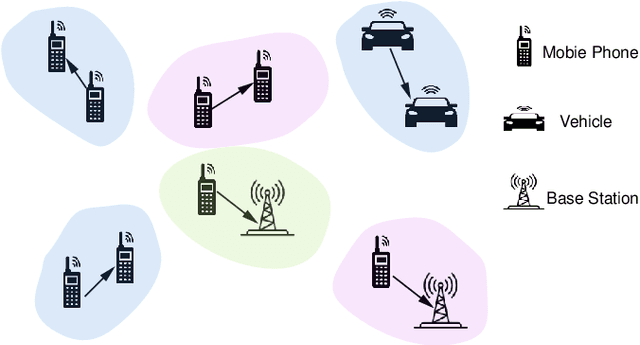
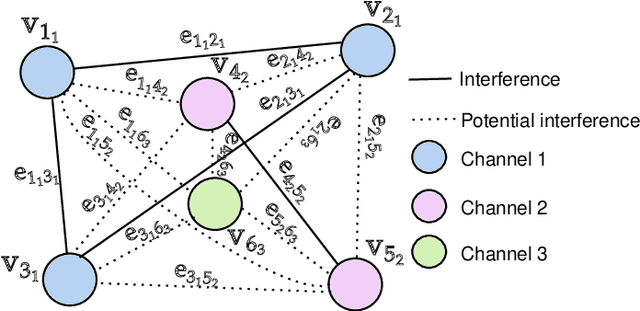
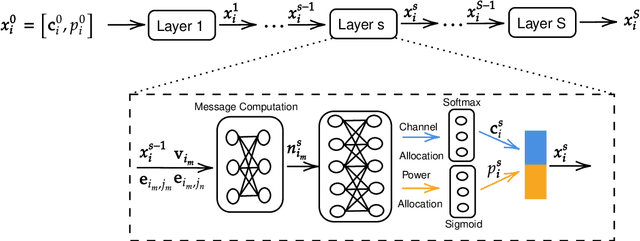
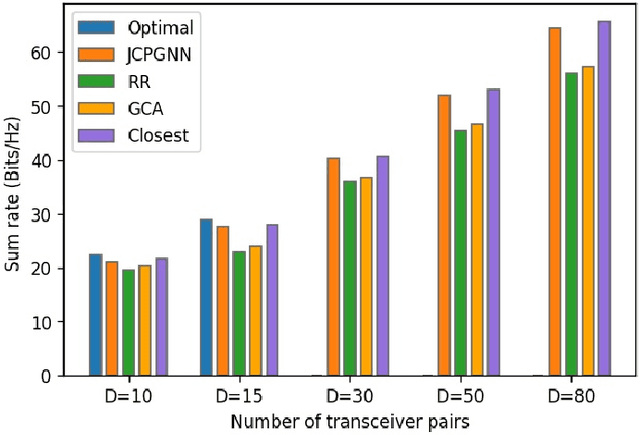
The optimal allocation of channels and power resources plays a crucial role in ensuring minimal interference, maximal data rates, and efficient energy utilisation. As a successful approach for tackling resource management problems in wireless networks, Graph Neural Networks (GNNs) have attracted a lot of attention. This article proposes a GNN-based algorithm to address the joint resource allocation problem in heterogeneous wireless networks. Concretely, we model the heterogeneous wireless network as a heterogeneous graph and then propose a graph neural network structure intending to allocate the available channels and transmit power to maximise the network throughput. Our proposed joint channel and power allocation graph neural network (JCPGNN) comprises a shared message computation layer and two task-specific layers, with a dedicated focus on channel and power allocation tasks, respectively. Comprehensive experiments demonstrate that the proposed algorithm achieves satisfactory performance but with higher computational efficiency compared to traditional optimisation algorithms.

Graph Neural Networks for Physical-Layer Security in Multi-User Flexible-Duplex Networks

This paper explores Physical-Layer Security (PLS) in Flexible Duplex (FlexD) networks, considering scenarios involving eavesdroppers. Our investigation revolves around the intricacies of the sum secrecy rate maximization problem, particularly when faced with coordinated and distributed eavesdroppers employing a Minimum Mean Square Error (MMSE) receiver. Our contributions include an iterative classical optimization solution and an unsupervised learning strategy based on Graph Neural Networks (GNNs). To the best of our knowledge, this work marks the initial exploration of GNNs for PLS applications. Additionally, we extend the GNN approach to address the absence of eavesdroppers' channel knowledge. Extensive numerical simulations highlight FlexD's superiority over Half-Duplex (HD) communications and the GNN approach's superiority over the classical method in both performance and time complexity.

Detection of Signals in Colored Noise: Leading Eigenvalue Test for Non-central $F$-matrices

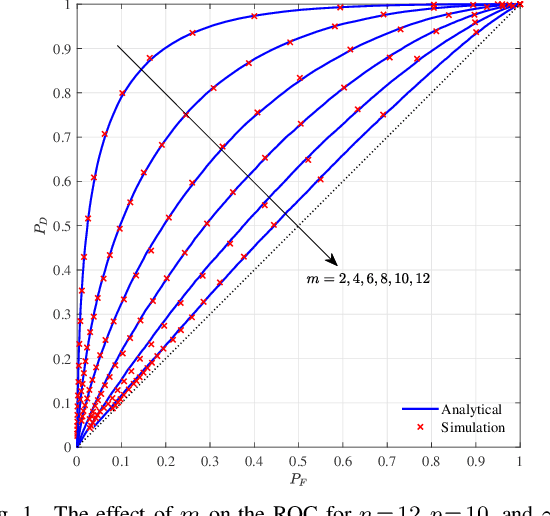
This paper investigates the signal detection problem in colored noise with an unknown covariance matrix. In particular, we focus on detecting an unknown non-random signal by capitalizing on the leading eigenvalue of the whitened sample covariance matrix as the test statistic (a.k.a. Roy's largest root test). Since the unknown signal is non-random, the whitened sample covariance matrix turns out to have a non-central $F$-distribution. This distribution assumes a singular or non-singular form depending on whether the number of observations $p\lessgtr$ the system dimensionality $m$. Therefore, we statistically characterize the leading eigenvalue of the singular and non-singular $F$-matrices by deriving their cumulative distribution functions (c.d.f.). Subsequently, they have been utilized in deriving the corresponding receiver operating characteristic (ROC) profiles. We also extend our analysis into the high dimensional domain. It turns out that, when the signal is sufficiently strong, the maximum eigenvalue can reliably detect it in this regime. Nevertheless, weak signals cannot be detected in the high dimensional regime with the leading eigenvalue.

OTFS based Joint Radar and Communication: Signal Analysis using the Ambiguity Function

Orthogonal time frequency space (OTFS) modulation has recently been identified as a suitable waveform for joint radar and communication systems. Focusing on the effect of data modulation on the radar sensing performance, we derive the ambiguity function (AF) of the OTFS waveform and characterize the radar global accuracy. We evaluate the behavior of the AF with respect to the distribution of the modulated data and derive an accurate approximation for the mean and variance of the AF, thus, approximating its distribution by a Rice distribution. Finally, we evaluate the global radar performance of the OTFS waveform with the OFDM waveform.

Performance Analysis of Relay Selection Schemes in Multi-Hop Decode-and-Forward Networks

This paper analyses the data rate achieved by various relay selection schemes in a single-user multi-hop relay network with decode-and-forward (DF) relaying. While the single-user relay selection problem is well studied in the literature, research on achievable rate maximization is limited to dual-hop networks and multi-hop networks with a single relay per hop. We fill this important gap by focusing on achievable rate maximization in multi-hop, multi-relay networks. First, we consider optimal relay selection and obtain two approximations to the achievable rate. Next, we consider three existing sub-optimal relay selection strategies namely hop-by-hop, ad-hoc and block-by-block relay selection and obtain exact expressions for the achievable rate under each of these strategies. We also extend the sliding window based relay selection to the DF relay network and derive an approximation to the achievable rate. Further, we investigate the impact of window size in sliding window based relay selection and show that a window size of three is sufficient to achieve most of the possible performance gains. Finally, we extend this analysis to a noise limited multi-user network where the number of available relay nodes is large compared to the number of users and derive approximations to the achievable sum-rate.

Generalized Eigenvalue Based Detection of Signals in Colored Noise: A Sample Deficient Analysis

This paper investigates the signal detection problem in colored noise with an unknown covariance matrix. To be specific, we consider a scenario in which the number of signal bearing samples ($n$) is strictly smaller than the dimensionality of the signal space ($m$). Our test statistic is the leading generalized eigenvalue of the whitened sample covariance matrix (a.k.a. $F$-matrix) which is constructed by whitening the signal bearing sample covariance matrix with noise-only sample covariance matrix. The sample deficiency (i.e., $m>n$) in turn makes this $F$-matrix rank deficient, thereby singular. Therefore, an exact statistical characterization of the leading generalized eigenvalue (l.g.e.) of a singular $F$-matrix is of paramount importance to assess the performance of the detector (i.e., the receiver operating characteristics (ROC)). To this end, we employ the powerful orthogonal polynomial approach to derive a new finite dimensional c.d.f. expression for the l.g.e. of a singular $F$-matrix. It turns out that when the noise only sample covariance matrix is nearly rank deficient and the signal-to-noise ratio is $O(m)$, the ROC profile converges to a limit.

Accelerating Graph Neural Networks via Edge Pruning for Power Allocation in Wireless Networks

Neural Networks (GNNs) have recently emerged as a promising approach to tackling power allocation problems in wireless networks. Since unpaired transmitters and receivers are often spatially distant, the distanced-based threshold is proposed to reduce the computation time by excluding or including the channel state information in GNNs. In this paper, we are the first to introduce a neighbour-based threshold approach to GNNs to reduce the time complexity. Furthermore, we conduct a comprehensive analysis of both distance-based and neighbour-based thresholds and provide recommendations for selecting the appropriate value in different communication channel scenarios. We design the corresponding distance-based and neighbour-based Graph Neural Networks with the aim of allocating transmit powers to maximise the network throughput. Our results show that our proposed GNNs offer significant advantages in terms of reducing time complexity while preserving strong performance. Besides, we show that by choosing a suitable threshold, the time complexity is reduced from O(|V|^2) to O(|V|), where |V| is the total number of transceiver pairs.