OTFS based Joint Radar and Communication: Signal Analysis using the Ambiguity Function

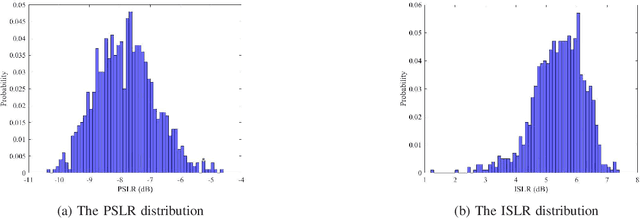
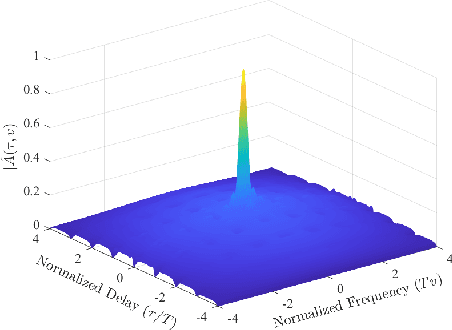
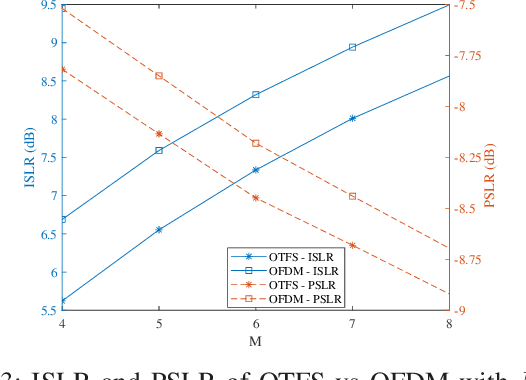
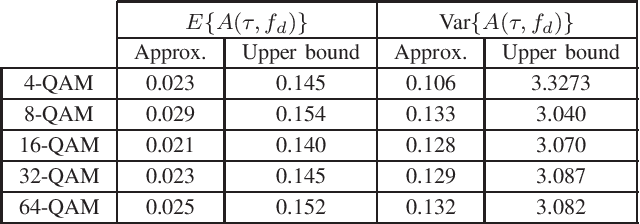
Orthogonal time frequency space (OTFS) modulation has recently been identified as a suitable waveform for joint radar and communication systems. Focusing on the effect of data modulation on the radar sensing performance, we derive the ambiguity function (AF) of the OTFS waveform and characterize the radar global accuracy. We evaluate the behavior of the AF with respect to the distribution of the modulated data and derive an accurate approximation for the mean and variance of the AF, thus, approximating its distribution by a Rice distribution. Finally, we evaluate the global radar performance of the OTFS waveform with the OFDM waveform.

Frequency Permutation Subsets for Joint Radar and Communication

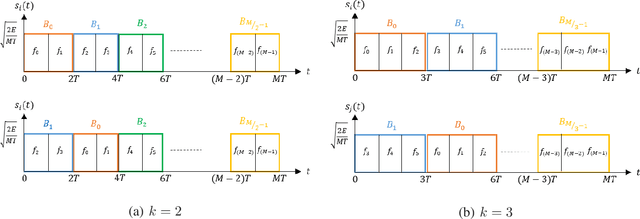
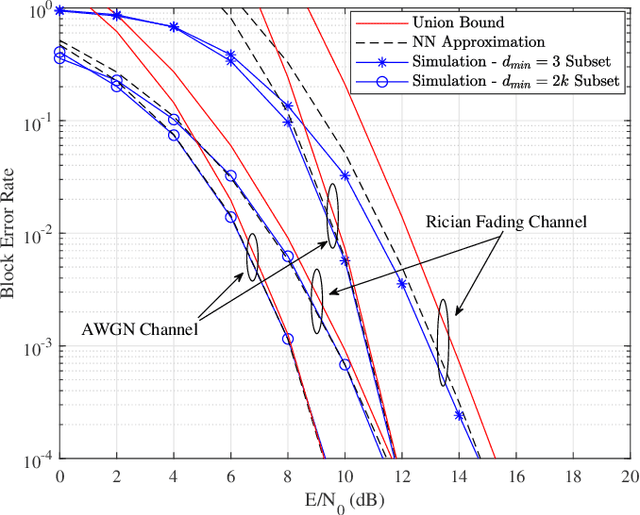
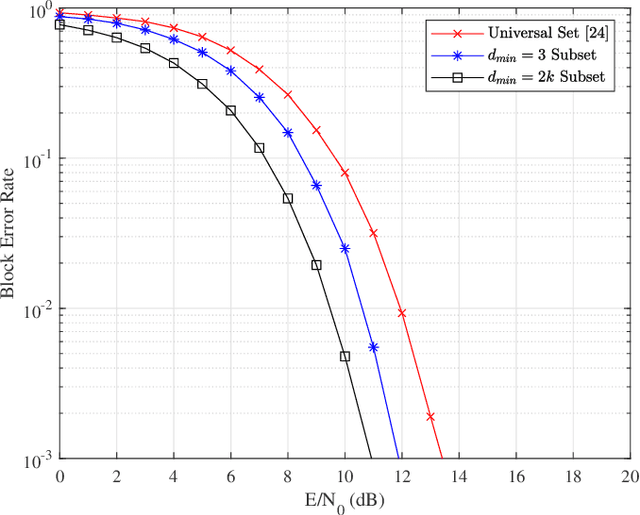
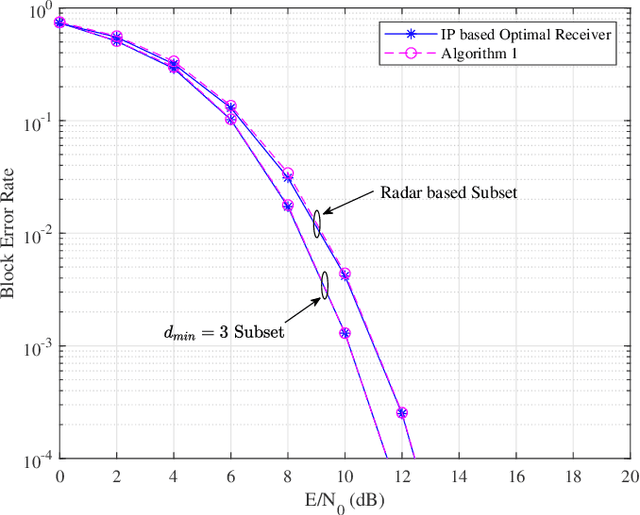
This paper focuses on waveform design for joint radar and communication systems and presents a new subset selection process to improve the communication error rate performance and global accuracy of radar sensing of the random stepped frequency permutation waveform. An optimal communication receiver based on integer programming is proposed to handle any subset of permutations followed by a more efficient sub-optimal receiver based on the Hungarian algorithm. Considering optimum maximum likelihood detection, the block error rate is analyzed under both additive white Gaussian noise and correlated Rician fading. We propose two methods to select a permutation subset with an improved block error rate and an efficient encoding scheme to map the information symbols to selected permutations under these subsets. From the radar perspective, the ambiguity function is analyzed with regards to the local and the global accuracy of target detection. Furthermore, a subset selection method to reduce the maximum sidelobe height is proposed by extending the properties of Costas arrays. Finally, the process of remapping the frequency tones to the symbol set used to generate permutations is introduced as a method to improve both the communication and radar performances of the selected permutation subset.

Combined Radar and Communications with Phase-Modulated Frequency Permutations

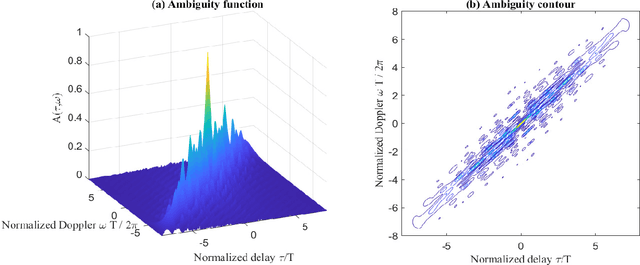
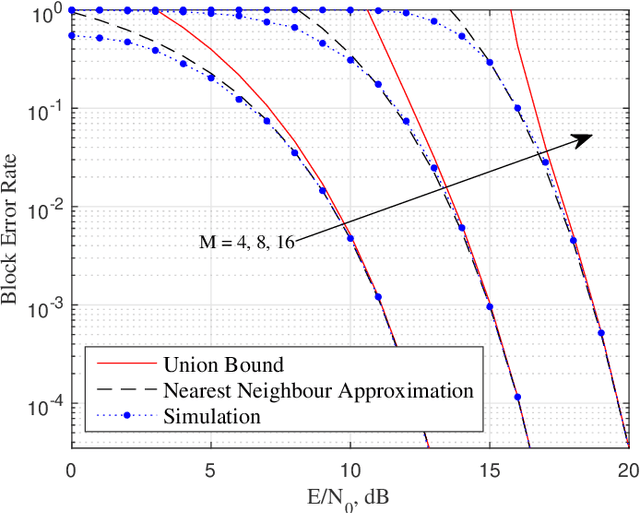
This paper focuses on the combined radar and communications problem and conducts a thorough analytical investigation on the effect of phase and frequency change on the communication and sensing functionality. First, we consider the classical stepped frequency radar waveform and modulate data using M-ary phase shift keying (MPSK). Two important analytical tools in radar waveform design, namely the ambiguity function (AF) and the Fisher information matrix (FIM) are derived, based on which, we make the important conclusion that MPSK modulation has a negligible effect on radar local accuracy. Next, we extend the analysis to incorporate frequency permutations and propose a new signalling scheme in which the mapping between incoming data and waveforms is performed based on an efficient combinatorial transform called the Lehmer code. We also provide an efficient communications receiver based on the Hungarian algorithm. From the communications perspective, we consider the optimal maximum likelihood (ML) detector and derive the union bound and nearest neighbour approximation on the block error probability. From the radar sensing perspective, we discuss the broader structure of the waveform based on the AF derivation and quantify the radar local accuracy based on the FIM.

Frequency Permutations for Joint Radar and Communications

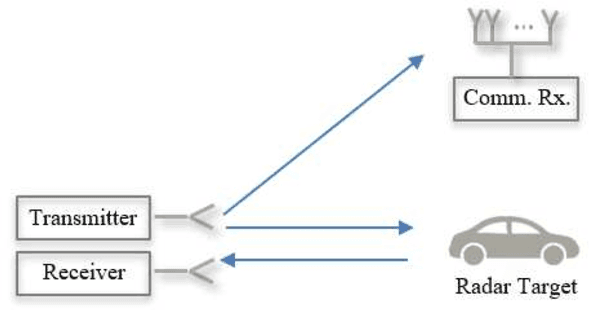
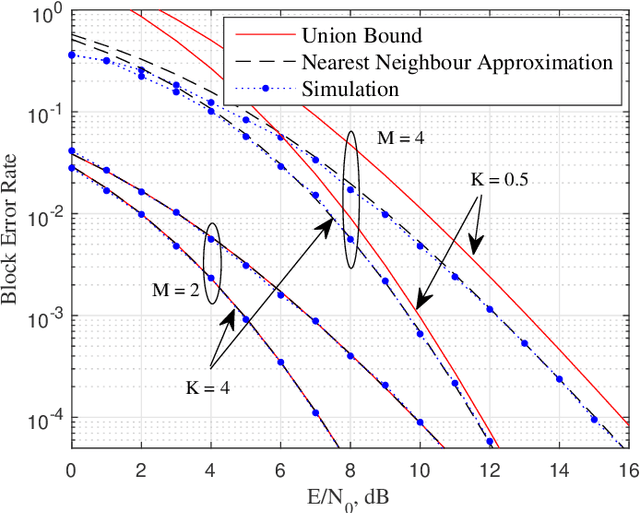
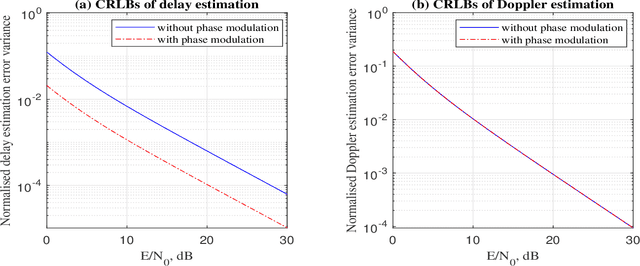
This paper presents a new joint radar and communication technique based on the classical stepped frequency radar waveform. The randomization in the waveform, which is achieved by using permutations of the sequence of frequency tones, is utilized for data transmission. A new signaling scheme is proposed in which the mapping between incoming data and waveforms is performed based on an efficient combinatorial transform called the Lehmer code. Considering the optimum maximum likelihood (ML) detection, the union bound and the nearest neighbour approximation on the communication block error probability is derived for communication in an additive white Gaussian noise (AWGN) channel. The results are further extended to incorporate the Rician fading channel model, of which the Rayleigh fading channel model is presented as a special case. Furthermore, an efficient communication receiver implementation is discussed based on the Hungarian algorithm which achieves optimum performance with much less operational complexity when compared to an exhaustive search. From the radar perspective, two key analytical tools, namely, the ambiguity function (AF) and the Fisher information matrix are derived. Furthermore, accurate approximations to the Cramer-Rao lower bounds (CRLBs) on the delay and Doppler estimation errors are derived based on which the range and velocity estimation accuracy of the waveform is analysed. Numerical examples are used to highlight the accuracy of the analysis and to illustrate the performance of the proposed waveform.