Combined Radar and Communications with Phase-Modulated Frequency Permutations

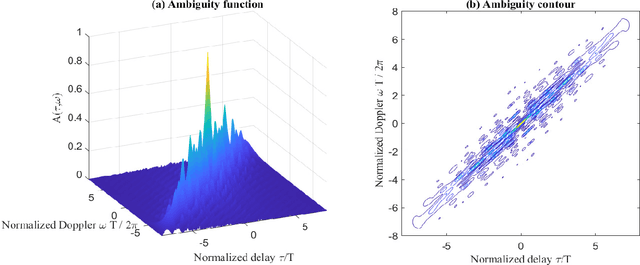
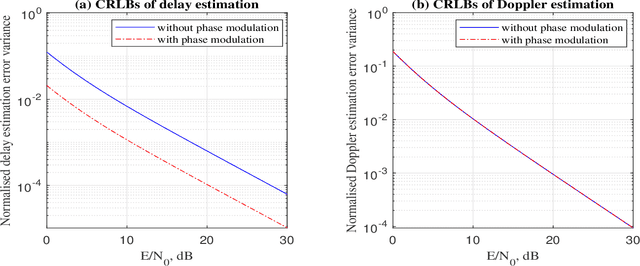
This paper focuses on the combined radar and communications problem and conducts a thorough analytical investigation on the effect of phase and frequency change on the communication and sensing functionality. First, we consider the classical stepped frequency radar waveform and modulate data using M-ary phase shift keying (MPSK). Two important analytical tools in radar waveform design, namely the ambiguity function (AF) and the Fisher information matrix (FIM) are derived, based on which, we make the important conclusion that MPSK modulation has a negligible effect on radar local accuracy. Next, we extend the analysis to incorporate frequency permutations and propose a new signalling scheme in which the mapping between incoming data and waveforms is performed based on an efficient combinatorial transform called the Lehmer code. We also provide an efficient communications receiver based on the Hungarian algorithm. From the communications perspective, we consider the optimal maximum likelihood (ML) detector and derive the union bound and nearest neighbour approximation on the block error probability. From the radar sensing perspective, we discuss the broader structure of the waveform based on the AF derivation and quantify the radar local accuracy based on the FIM.

Frequency Permutations for Joint Radar and Communications

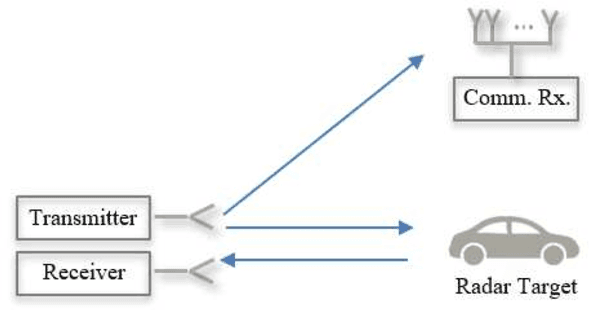
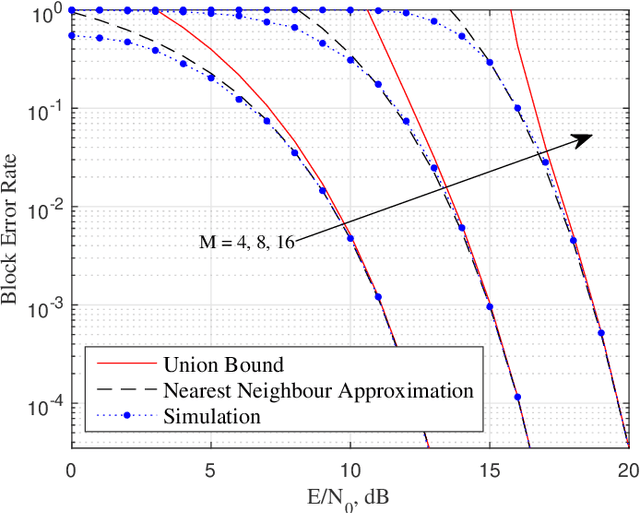
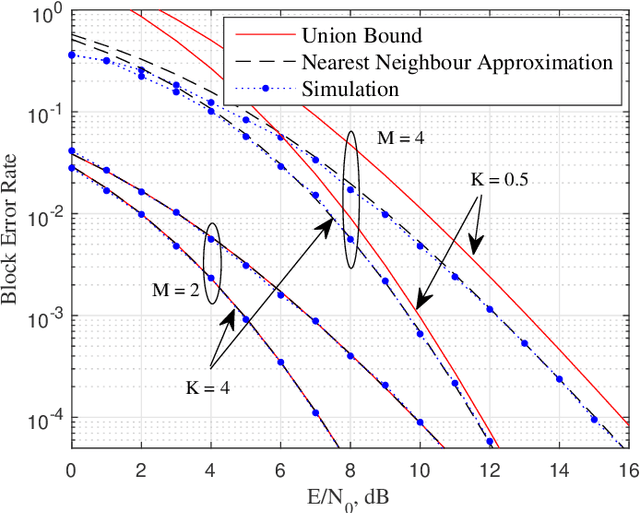
This paper presents a new joint radar and communication technique based on the classical stepped frequency radar waveform. The randomization in the waveform, which is achieved by using permutations of the sequence of frequency tones, is utilized for data transmission. A new signaling scheme is proposed in which the mapping between incoming data and waveforms is performed based on an efficient combinatorial transform called the Lehmer code. Considering the optimum maximum likelihood (ML) detection, the union bound and the nearest neighbour approximation on the communication block error probability is derived for communication in an additive white Gaussian noise (AWGN) channel. The results are further extended to incorporate the Rician fading channel model, of which the Rayleigh fading channel model is presented as a special case. Furthermore, an efficient communication receiver implementation is discussed based on the Hungarian algorithm which achieves optimum performance with much less operational complexity when compared to an exhaustive search. From the radar perspective, two key analytical tools, namely, the ambiguity function (AF) and the Fisher information matrix are derived. Furthermore, accurate approximations to the Cramer-Rao lower bounds (CRLBs) on the delay and Doppler estimation errors are derived based on which the range and velocity estimation accuracy of the waveform is analysed. Numerical examples are used to highlight the accuracy of the analysis and to illustrate the performance of the proposed waveform.

Knowledge engineering mixed-integer linear programming: constraint typology

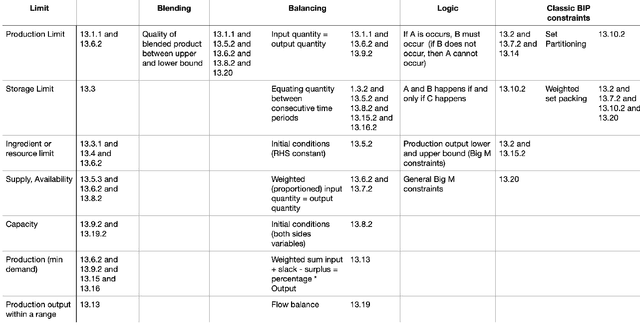
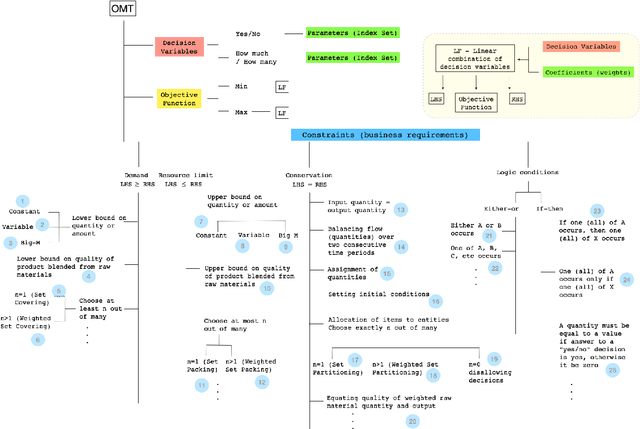
In this paper, we investigate the constraint typology of mixed-integer linear programming MILP formulations. MILP is a commonly used mathematical programming technique for modelling and solving real-life scheduling, routing, planning, resource allocation, timetabling optimization problems, providing optimized business solutions for industry sectors such as: manufacturing, agriculture, defence, healthcare, medicine, energy, finance, and transportation. Despite the numerous real-life Combinatorial Optimization Problems found and solved, and millions yet to be discovered and formulated, the number of types of constraints, the building blocks of a MILP, is relatively much smaller. In the search of a suitable machine readable knowledge representation for MILPs, we propose an optimization modelling tree built based upon an MILP ontology that can be used as a guidance for automated systems to elicit an MILP model from end-users on their combinatorial business optimization problems.

Inverse Cognitive Radar -- A Revealed Preferences Approach

We consider an adversarial signal processing problem involving "us" versus an "enemy" cognitive radar. The enemy's cognitive radar observes our state in noise; uses a tracker to update its posterior distribution of our state and then chooses an action based on this posterior. Given knowledge of "our" state and the observed sequence of actions taken by the enemy's radar, we consider three problems: (i) Are the enemy radar's actions consistent with optimizing a monotone utility function (i.e., is the cognitive radar behavior rational in an economics sense). If so how can we estimate the adversary's cognitive radar's utility function that is consistent with its actions. (ii) How to construct a statistical detection test for utility maximization when we observe the enemy radar's actions in noise? (iii) How can we optimally probe the enemy's radar by choosing our state to minimize the Type 2 error of detecting if the radar is deploying an economic rational strategy, subject to a constraint on the Type 1 detection error? "Our" state can be viewed as a probe signal which causes the enemy's radar to act; so choosing the optimal state sequence is an input design problem. The main analysis framework used in this paper is that of revealed preferences from microeconomics.

Hypothesis Testing in Feedforward Networks with Broadcast Failures

Consider a countably infinite set of nodes, which sequentially make decisions between two given hypotheses. Each node takes a measurement of the underlying truth, observes the decisions from some immediate predecessors, and makes a decision between the given hypotheses. We consider two classes of broadcast failures: 1) each node broadcasts a decision to the other nodes, subject to random erasure in the form of a binary erasure channel; 2) each node broadcasts a randomly flipped decision to the other nodes in the form of a binary symmetric channel. We are interested in whether there exists a decision strategy consisting of a sequence of likelihood ratio tests such that the node decisions converge in probability to the underlying truth. In both cases, we show that if each node only learns from a bounded number of immediate predecessors, then there does not exist a decision strategy such that the decisions converge in probability to the underlying truth. However, in case 1, we show that if each node learns from an unboundedly growing number of predecessors, then the decisions converge in probability to the underlying truth, even when the erasure probabilities converge to 1. We also derive the convergence rate of the error probability. In case 2, we show that if each node learns from all of its previous predecessors, then the decisions converge in probability to the underlying truth when the flipping probabilities of the binary symmetric channels are bounded away from 1/2. In the case where the flipping probabilities converge to 1/2, we derive a necessary condition on the convergence rate of the flipping probabilities such that the decisions still converge to the underlying truth. We also explicitly characterize the relationship between the convergence rate of the error probability and the convergence rate of the flipping probabilities.

Learning in Hierarchical Social Networks

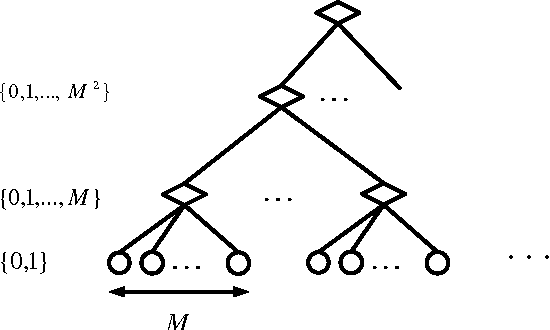
We study a social network consisting of agents organized as a hierarchical M-ary rooted tree, common in enterprise and military organizational structures. The goal is to aggregate information to solve a binary hypothesis testing problem. Each agent at a leaf of the tree, and only such an agent, makes a direct measurement of the underlying true hypothesis. The leaf agent then makes a decision and sends it to its supervising agent, at the next level of the tree. Each supervising agent aggregates the decisions from the M members of its group, produces a summary message, and sends it to its supervisor at the next level, and so on. Ultimately, the agent at the root of the tree makes an overall decision. We derive upper and lower bounds for the Type I and II error probabilities associated with this decision with respect to the number of leaf agents, which in turn characterize the converge rates of the Type I, Type II, and total error probabilities. We also provide a message-passing scheme involving non-binary message alphabets and characterize the exponent of the error probability with respect to the message alphabet size.