Single-Pixel Image Reconstruction Based on Block Compressive Sensing and Deep Learning

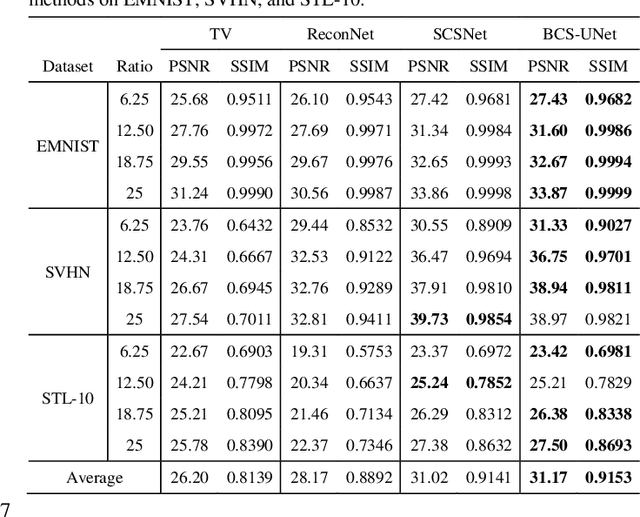
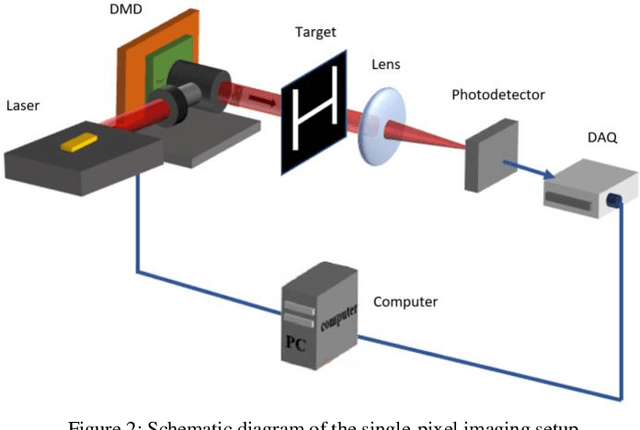
Single-pixel imaging (SPI) is a novel imaging technique whose working principle is based on the compressive sensing (CS) theory. In SPI, data is obtained through a series of compressive measurements and the corresponding image is reconstructed. Typically, the reconstruction algorithm such as basis pursuit relies on the sparsity assumption in images. However, recent advances in deep learning have found its uses in reconstructing CS images. Despite showing a promising result in simulations, it is often unclear how such an algorithm can be implemented in an actual SPI setup. In this paper, we demonstrate the use of deep learning on the reconstruction of SPI images in conjunction with block compressive sensing (BCS). We also proposed a novel reconstruction model based on convolutional neural networks that outperforms other competitive CS reconstruction algorithms. Besides, by incorporating BCS in our deep learning model, we were able to reconstruct images of any size above a certain smallest image size. In addition, we show that our model is capable of reconstructing images obtained from an SPI setup while being priorly trained on natural images, which can be vastly different from the SPI images. This opens up opportunity for the feasibility of pretrained deep learning models for CS reconstructions of images from various domain areas.

Well-Conditioned Linear Minimum Mean Square Error Estimation

Linear minimum mean square error (LMMSE) estimation is often ill-conditioned, suggesting that unconstrained minimization of the mean square error is an inadequate principle for filter design. To address this, we first develop a unifying framework for studying constrained LMMSE estimation problems. Using this framework, we expose an important structural property of constrained LMMSE filters: They generally involve an inherent preconditioning step. This parameterizes all such filters only by their preconditioners. Moreover, each filters is invariant to invertible linear transformations of its preconditioner. We then clarify that merely constraining the rank of the filter does not suitably address the problem of ill-conditioning. Instead, we adopt a constraint that explicitly requires solutions to be well-conditioned in a certain specific sense. We introduce two well-conditioned filters and show that they converge to the unconstrained LMMSE filter as their truncated-power loss goes to zero, at the same rate as the low-rank Wiener filter. We also show extensions to the case of weighted trace and determinant of the error covariance as objective functions. Finally, we show quantitative results with historical VIX data to demonstrate that our two well-conditioned filters have stable performance while the standard LMMSE filter deteriorates with increasing condition number.

Automated Pavement Crack Segmentation Using Fully Convolutional U-Net with a Pretrained ResNet-34 Encoder

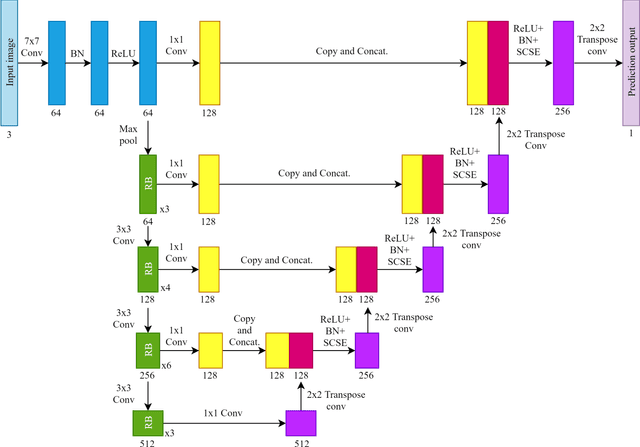
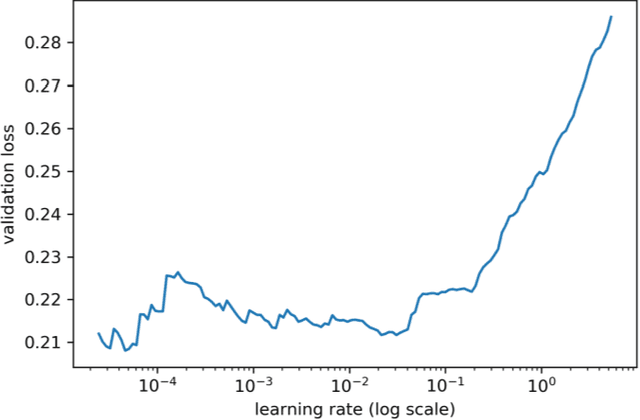
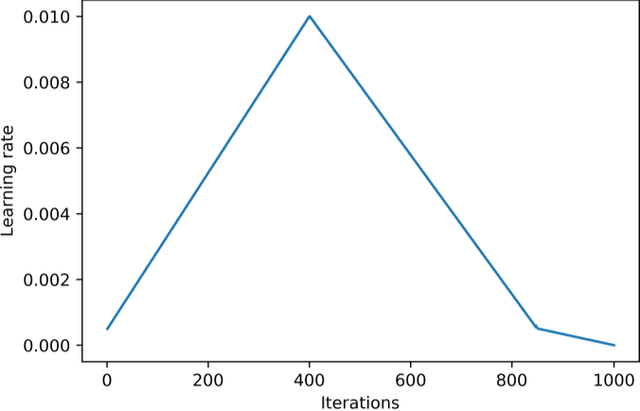
Automated pavement crack segmentation is a challenging task because of inherent irregular patterns and lighting conditions, in addition to the presence of noise in images. Conventional approaches require a substantial amount of feature engineering to differentiate crack regions from non-affected regions. In this paper, we propose a deep learning technique based on a convolutional neural network to perform segmentation tasks on pavement crack images. Our approach requires minimal feature engineering compared to other machine learning techniques. The proposed neural network architecture is a modified U-Net in which the encoder is replaced with a pretrained ResNet-34 network. To minimize the dice coefficient loss function, we optimize the parameters in the neural network by using an adaptive moment optimizer called AdamW. Additionally, we use a systematic method to find the optimum learning rate instead of doing parametric sweeps. We used a "one-cycle" training schedule based on cyclical learning rates to speed up the convergence. We evaluated the performance of our convolutional neural network on CFD, a pavement crack image dataset. Our method achieved an F1 score of about 96%. This is the best performance among all other algorithms tested on this dataset, outperforming the previous best method by a 1.7% margin.

Decision Automation for Electric Power Network Recovery

Critical infrastructure systems such as electric power networks, water networks, and transportation systems play a major role in the welfare of any community. In the aftermath of disasters, their recovery is of paramount importance; orderly and efficient recovery involves the assignment of limited resources (a combination of human repair workers and machines) to repair damaged infrastructure components. The decision maker must also deal with uncertainty in the outcome of the resource-allocation actions during recovery. The manual assignment of resources seldom is optimal despite the expertise of the decision maker because of the large number of choices and uncertainties in consequences of sequential decisions. This combinatorial assignment problem under uncertainty is known to be \mbox{NP-hard}. We propose a novel decision technique that addresses the massive number of decision choices for large-scale real-world problems; in addition, our method also features an experiential learning component that adaptively determines the utilization of the computational resources based on the performance of a small number of choices. Our framework is closed-loop, and naturally incorporates all the attractive features of such a decision-making system. In contrast to myopic approaches, which do not account for the future effects of the current choices, our methodology has an anticipatory learning component that effectively incorporates \emph{lookahead} into the solutions. To this end, we leverage the theory of regression analysis, Markov decision processes (MDPs), multi-armed bandits, and stochastic models of community damage from natural disasters to develop a method for near-optimal recovery of communities. Our method contributes to the general problem of MDPs with massive action spaces with application to recovery of communities affected by hazards.

Ranking and Selection as Stochastic Control

Under a Bayesian framework, we formulate the fully sequential sampling and selection decision in statistical ranking and selection as a stochastic control problem, and derive the associated Bellman equation. Using value function approximation, we derive an approximately optimal allocation policy. We show that this policy is not only computationally efficient but also possesses both one-step-ahead and asymptotic optimality for independent normal sampling distributions. Moreover, the proposed allocation policy is easily generalizable in the approximate dynamic programming paradigm.

Hypothesis Testing in Feedforward Networks with Broadcast Failures

Consider a countably infinite set of nodes, which sequentially make decisions between two given hypotheses. Each node takes a measurement of the underlying truth, observes the decisions from some immediate predecessors, and makes a decision between the given hypotheses. We consider two classes of broadcast failures: 1) each node broadcasts a decision to the other nodes, subject to random erasure in the form of a binary erasure channel; 2) each node broadcasts a randomly flipped decision to the other nodes in the form of a binary symmetric channel. We are interested in whether there exists a decision strategy consisting of a sequence of likelihood ratio tests such that the node decisions converge in probability to the underlying truth. In both cases, we show that if each node only learns from a bounded number of immediate predecessors, then there does not exist a decision strategy such that the decisions converge in probability to the underlying truth. However, in case 1, we show that if each node learns from an unboundedly growing number of predecessors, then the decisions converge in probability to the underlying truth, even when the erasure probabilities converge to 1. We also derive the convergence rate of the error probability. In case 2, we show that if each node learns from all of its previous predecessors, then the decisions converge in probability to the underlying truth when the flipping probabilities of the binary symmetric channels are bounded away from 1/2. In the case where the flipping probabilities converge to 1/2, we derive a necessary condition on the convergence rate of the flipping probabilities such that the decisions still converge to the underlying truth. We also explicitly characterize the relationship between the convergence rate of the error probability and the convergence rate of the flipping probabilities.

Learning in Hierarchical Social Networks

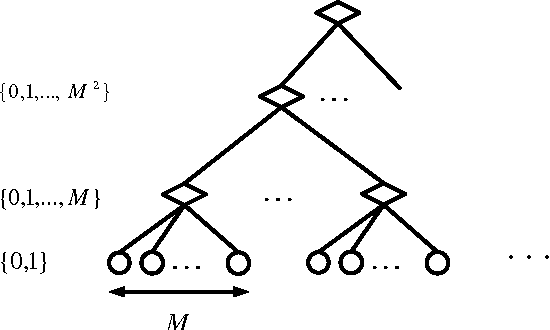
We study a social network consisting of agents organized as a hierarchical M-ary rooted tree, common in enterprise and military organizational structures. The goal is to aggregate information to solve a binary hypothesis testing problem. Each agent at a leaf of the tree, and only such an agent, makes a direct measurement of the underlying true hypothesis. The leaf agent then makes a decision and sends it to its supervising agent, at the next level of the tree. Each supervising agent aggregates the decisions from the M members of its group, produces a summary message, and sends it to its supervisor at the next level, and so on. Ultimately, the agent at the root of the tree makes an overall decision. We derive upper and lower bounds for the Type I and II error probabilities associated with this decision with respect to the number of leaf agents, which in turn characterize the converge rates of the Type I, Type II, and total error probabilities. We also provide a message-passing scheme involving non-binary message alphabets and characterize the exponent of the error probability with respect to the message alphabet size.