Stephen D. Howard
Learning in Hierarchical Social Networks
Nov 21, 2012

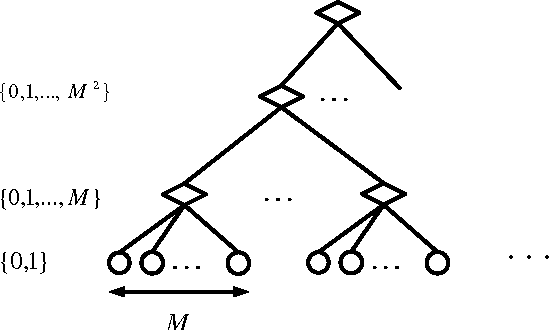
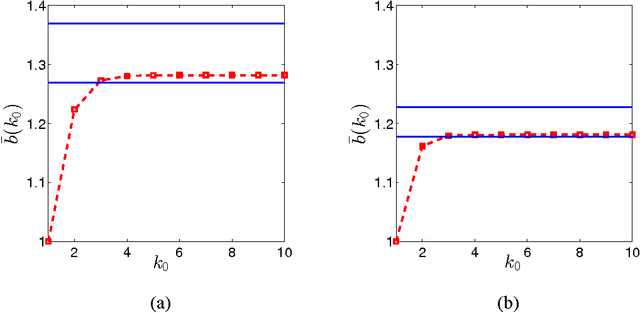
Abstract:We study a social network consisting of agents organized as a hierarchical M-ary rooted tree, common in enterprise and military organizational structures. The goal is to aggregate information to solve a binary hypothesis testing problem. Each agent at a leaf of the tree, and only such an agent, makes a direct measurement of the underlying true hypothesis. The leaf agent then makes a decision and sends it to its supervising agent, at the next level of the tree. Each supervising agent aggregates the decisions from the M members of its group, produces a summary message, and sends it to its supervisor at the next level, and so on. Ultimately, the agent at the root of the tree makes an overall decision. We derive upper and lower bounds for the Type I and II error probabilities associated with this decision with respect to the number of leaf agents, which in turn characterize the converge rates of the Type I, Type II, and total error probabilities. We also provide a message-passing scheme involving non-binary message alphabets and characterize the exponent of the error probability with respect to the message alphabet size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge