Low-Rank-Based Approximate Computation with Memristors

Memristor crossbars enable vector-matrix multiplication (VMM), and are promising for low-power applications. However, it can be difficult to write the memristor conductance values exactly. To improve the accuracy of VMM, we propose a scheme based on low-rank matrix approximation. Specifically, singular value decomposition (SVD) is first applied to obtain a low-rank approximation of the target matrix, which is then factored into a pair of smaller matrices. Subsequently, a two-step serial VMM is executed, where the stochastic write errors are mitigated through step-wise averaging. To evaluate the performance of the proposed scheme, we derive a general expression for the resulting computation error and provide an asymptotic analysis under a prescribed singular-value profile, which reveals how the error scales with matrix size and rank. Both analytical and numerical results confirm the superiority of the proposed scheme compared with the benchmark scheme.

Graph Neural Networks for Resource Allocation in Multi-Channel Wireless Networks

As the number of mobile devices continues to grow, interference has become a major bottleneck in improving data rates in wireless networks. Efficient joint channel and power allocation (JCPA) is crucial for managing interference. In this paper, we first propose an enhanced WMMSE (eWMMSE) algorithm to solve the JCPA problem in multi-channel wireless networks. To reduce the computational complexity of iterative optimization, we further introduce JCPGNN-M, a graph neural network-based solution that enables simultaneous multi-channel allocation for each user. We reformulate the problem as a Lagrangian function, which allows us to enforce the total power constraints systematically. Our solution involves combining this Lagrangian framework with GNNs and iteratively updating the Lagrange multipliers and resource allocation scheme. Unlike existing GNN-based methods that limit each user to a single channel, JCPGNN-M supports efficient spectrum reuse and scales well in dense network scenarios. Simulation results show that JCPGNN-M achieves better data rate compared to eWMMSE. Meanwhile, the inference time of JCPGNN-M is much lower than eWMMS, and it can generalize well to larger networks.

Emergence of Computational Structure in a Neural Network Physics Simulator

Neural networks often have identifiable computational structures - components of the network which perform an interpretable algorithm or task - but the mechanisms by which these emerge and the best methods for detecting these structures are not well understood. In this paper we investigate the emergence of computational structure in a transformer-like model trained to simulate the physics of a particle system, where the transformer's attention mechanism is used to transfer information between particles. We show that (a) structures emerge in the attention heads of the transformer which learn to detect particle collisions, (b) the emergence of these structures is associated to degenerate geometry in the loss landscape, and (c) the dynamics of this emergence follows a power law. This suggests that these components are governed by a degenerate "effective potential". These results have implications for the convergence time of computational structure within neural networks and suggest that the emergence of computational structure can be detected by studying the dynamics of network components.

Non-Asymptotic Bounds for Closed-Loop Identification of Unstable Nonlinear Stochastic Systems

We consider the problem of least squares parameter estimation from single-trajectory data for discrete-time, unstable, closed-loop nonlinear stochastic systems, with linearly parameterised uncertainty. Assuming a region of the state space produces informative data, and the system is sub-exponentially unstable, we establish non-asymptotic guarantees on the estimation error at times where the state trajectory evolves in this region. If the whole state space is informative, high probability guarantees on the error hold for all times. Examples are provided where our results are useful for analysis, but existing results are not.

GNN-Based Joint Channel and Power Allocation in Heterogeneous Wireless Networks

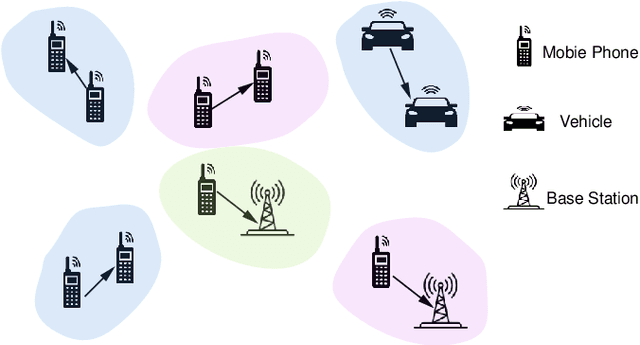
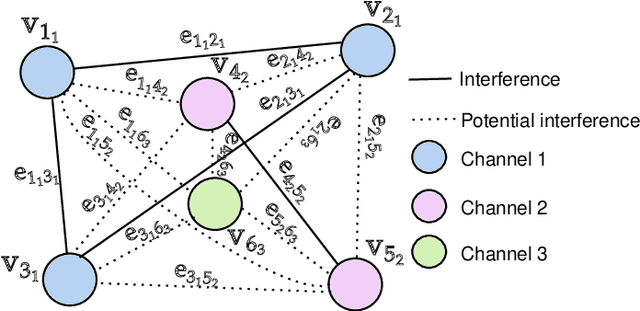
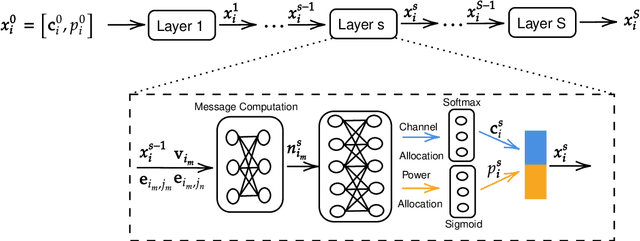
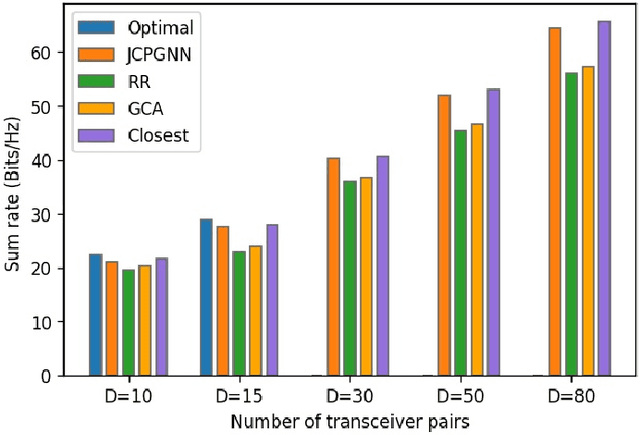
The optimal allocation of channels and power resources plays a crucial role in ensuring minimal interference, maximal data rates, and efficient energy utilisation. As a successful approach for tackling resource management problems in wireless networks, Graph Neural Networks (GNNs) have attracted a lot of attention. This article proposes a GNN-based algorithm to address the joint resource allocation problem in heterogeneous wireless networks. Concretely, we model the heterogeneous wireless network as a heterogeneous graph and then propose a graph neural network structure intending to allocate the available channels and transmit power to maximise the network throughput. Our proposed joint channel and power allocation graph neural network (JCPGNN) comprises a shared message computation layer and two task-specific layers, with a dedicated focus on channel and power allocation tasks, respectively. Comprehensive experiments demonstrate that the proposed algorithm achieves satisfactory performance but with higher computational efficiency compared to traditional optimisation algorithms.

Accelerating Graph Neural Networks via Edge Pruning for Power Allocation in Wireless Networks

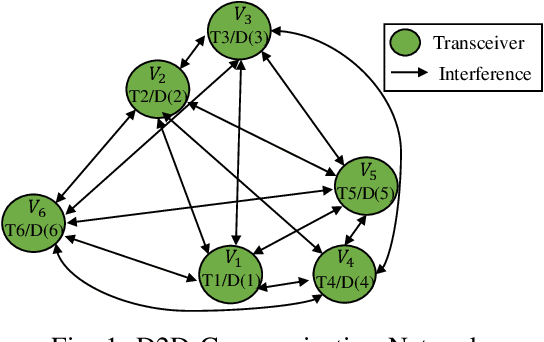
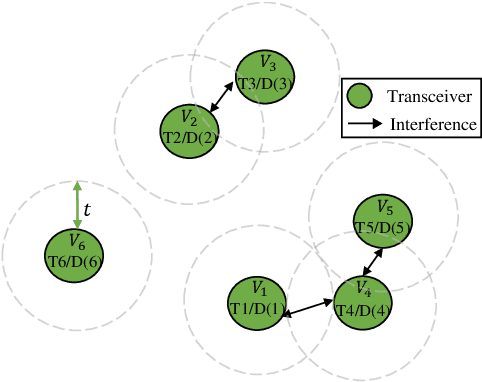
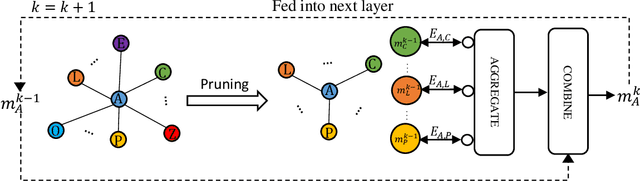
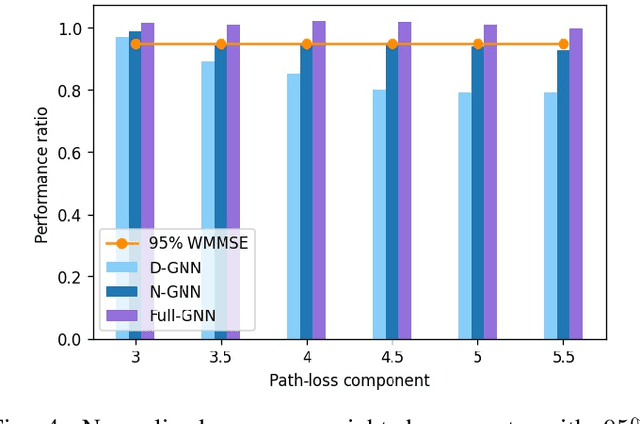
Neural Networks (GNNs) have recently emerged as a promising approach to tackling power allocation problems in wireless networks. Since unpaired transmitters and receivers are often spatially distant, the distanced-based threshold is proposed to reduce the computation time by excluding or including the channel state information in GNNs. In this paper, we are the first to introduce a neighbour-based threshold approach to GNNs to reduce the time complexity. Furthermore, we conduct a comprehensive analysis of both distance-based and neighbour-based thresholds and provide recommendations for selecting the appropriate value in different communication channel scenarios. We design the corresponding distance-based and neighbour-based Graph Neural Networks with the aim of allocating transmit powers to maximise the network throughput. Our results show that our proposed GNNs offer significant advantages in terms of reducing time complexity while preserving strong performance. Besides, we show that by choosing a suitable threshold, the time complexity is reduced from O(|V|^2) to O(|V|), where |V| is the total number of transceiver pairs.

Stability Bounds for Learning-Based Adaptive Control of Discrete-Time Multi-Dimensional Stochastic Linear Systems with Input Constraints

We consider the problem of adaptive stabilization for discrete-time, multi-dimensional linear systems with bounded control input constraints and unbounded stochastic disturbances, where the parameters of the true system are unknown. To address this challenge, we propose a certainty-equivalent control scheme which combines online parameter estimation with saturated linear control. We establish the existence of a high probability stability bound on the closed-loop system, under additional assumptions on the system and noise processes. Finally, numerical examples are presented to illustrate our results.

Graph Neural Networks for Power Allocation in Wireless Networks with Full Duplex Nodes

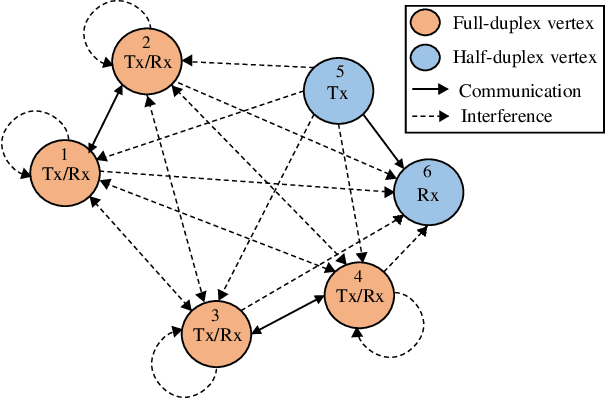
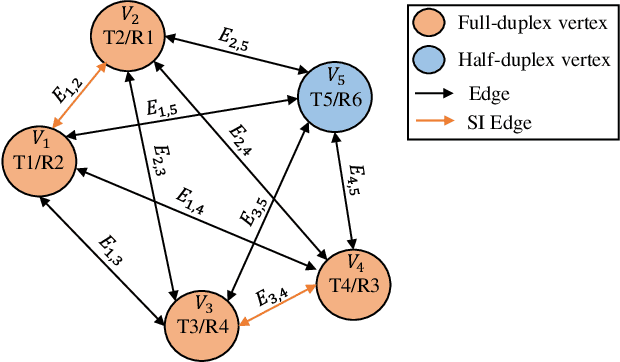
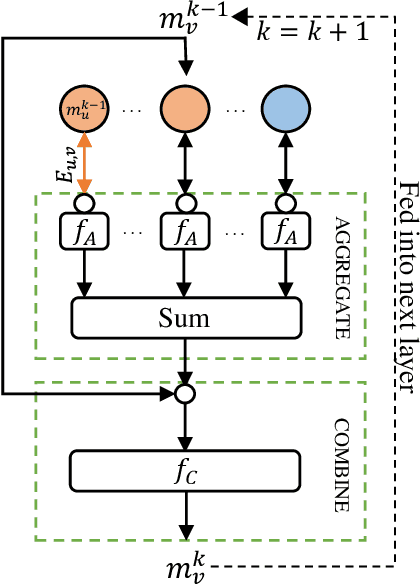
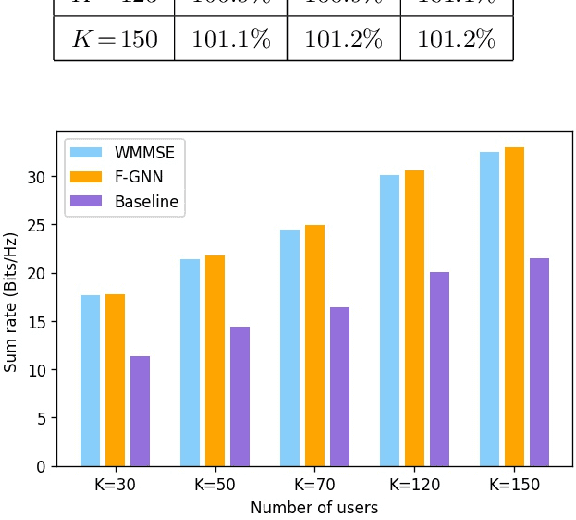
Due to mutual interference between users, power allocation problems in wireless networks are often non-convex and computationally challenging. Graph neural networks (GNNs) have recently emerged as a promising approach to tackling these problems and an approach that exploits the underlying topology of wireless networks. In this paper, we propose a novel graph representation method for wireless networks that include full-duplex (FD) nodes. We then design a corresponding FD Graph Neural Network (F-GNN) with the aim of allocating transmit powers to maximise the network throughput. Our results show that our F-GNN achieves state-of-art performance with significantly less computation time. Besides, F-GNN offers an excellent trade-off between performance and complexity compared to classical approaches. We further refine this trade-off by introducing a distance-based threshold for inclusion or exclusion of edges in the network. We show that an appropriately chosen threshold reduces required training time by roughly 20% with a relatively minor loss in performance.

On the tightness of information-theoretic bounds on generalization error of learning algorithms

A recent line of works, initiated by Russo and Xu, has shown that the generalization error of a learning algorithm can be upper bounded by information measures. In most of the relevant works, the convergence rate of the expected generalization error is in the form of $O(\sqrt{\lambda/n})$ where $\lambda$ is some information-theoretic quantities such as the mutual information or conditional mutual information between the data and the learned hypothesis. However, such a learning rate is typically considered to be ``slow", compared to a ``fast rate" of $O(\lambda/n)$ in many learning scenarios. In this work, we first show that the square root does not necessarily imply a slow rate, and a fast rate result can still be obtained using this bound under appropriate assumptions. Furthermore, we identify the critical conditions needed for the fast rate generalization error, which we call the $(\eta,c)$-central condition. Under this condition, we give information-theoretic bounds on the generalization error and excess risk, with a fast convergence rate for specific learning algorithms such as empirical risk minimization and its regularized version. Finally, several analytical examples are given to show the effectiveness of the bounds.

On the Value of Stochastic Side Information in Online Learning

We study the effectiveness of stochastic side information in deterministic online learning scenarios. We propose a forecaster to predict a deterministic sequence where its performance is evaluated against an expert class. We assume that certain stochastic side information is available to the forecaster but not the experts. We define the minimax expected regret for evaluating the forecasters performance, for which we obtain both upper and lower bounds. Consequently, our results characterize the improvement in the regret due to the stochastic side information. Compared with the classical online learning problem with regret scales with O(\sqrt(n)), the regret can be negative when the stochastic side information is more powerful than the experts. To illustrate, we apply the proposed bounds to two concrete examples of different types of side information.