Non-Asymptotic Bounds for Closed-Loop Identification of Unstable Nonlinear Stochastic Systems

We consider the problem of least squares parameter estimation from single-trajectory data for discrete-time, unstable, closed-loop nonlinear stochastic systems, with linearly parameterised uncertainty. Assuming a region of the state space produces informative data, and the system is sub-exponentially unstable, we establish non-asymptotic guarantees on the estimation error at times where the state trajectory evolves in this region. If the whole state space is informative, high probability guarantees on the error hold for all times. Examples are provided where our results are useful for analysis, but existing results are not.

Towards Fast and Safety-Guaranteed Trajectory Planning and Tracking for Time-Varying Systems

When deploying autonomous systems in unknown and changing environments, it is critical that their motion planning and control algorithms are computationally efficient and can be reapplied online in real time, whilst providing theoretical safety guarantees in the presence of disturbances. The satisfaction of these objectives becomes more challenging when considering time-varying dynamics and disturbances, which arise in real-world contexts. We develop methods with the potential to address these issues by applying an offline-computed safety guaranteeing controller on a physical system, to track a virtual system that evolves through a trajectory that is replanned online, accounting for constraints updated online. The first method we propose is designed for general time-varying systems over a finite horizon. Our second method overcomes the finite horizon restriction for periodic systems. We simulate our algorithms on a case study of an autonomous underwater vehicle subject to wave disturbances.

Task-Oriented Koopman-Based Control with Contrastive Encoder

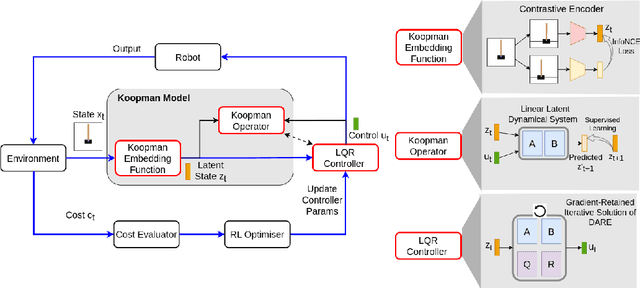
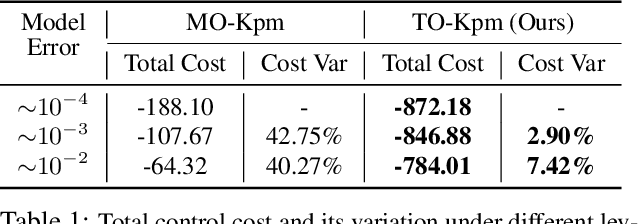
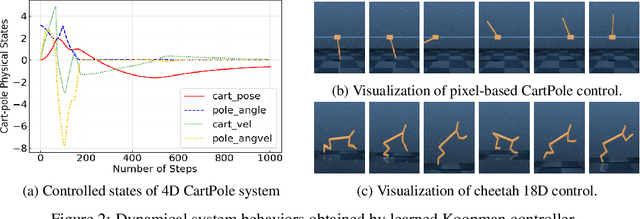
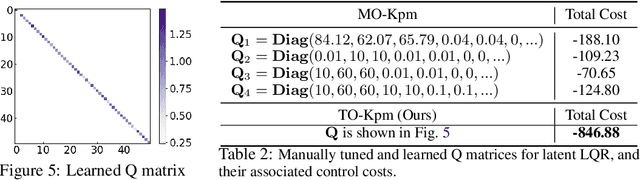
We present task-oriented Koopman-based control that utilizes end-to-end reinforcement learning and contrastive encoder to simultaneously learn the Koopman latent embedding, operator and associated linear controller within an iterative loop. By prioritizing the task cost as main objective for controller learning, we reduce the reliance of controller design on a well-identified model, which extends Koopman control beyond low-dimensional systems to high-dimensional, complex nonlinear systems, including pixel-based scenarios.

Stability Bounds for Learning-Based Adaptive Control of Discrete-Time Multi-Dimensional Stochastic Linear Systems with Input Constraints

We consider the problem of adaptive stabilization for discrete-time, multi-dimensional linear systems with bounded control input constraints and unbounded stochastic disturbances, where the parameters of the true system are unknown. To address this challenge, we propose a certainty-equivalent control scheme which combines online parameter estimation with saturated linear control. We establish the existence of a high probability stability bound on the closed-loop system, under additional assumptions on the system and noise processes. Finally, numerical examples are presented to illustrate our results.

Learning-Based Adaptive Control for Stochastic Linear Systems with Input Constraints

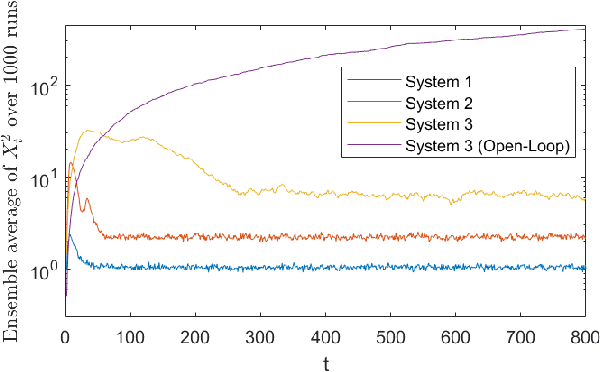
We propose a certainty-equivalence scheme for adaptive control of scalar linear systems subject to additive, i.i.d. Gaussian disturbances and bounded control input constraints, without requiring prior knowledge of the bounds of the system parameters, nor the control direction. Assuming that the system is at-worst marginally stable, mean square boundedness of the closed-loop system states is proven. Lastly, numerical examples are presented to illustrate our results.

Safety-guaranteed trajectory planning and control based on GP estimation for unmanned surface vessels

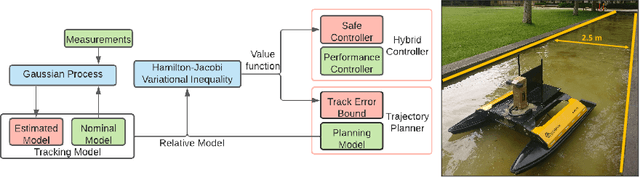
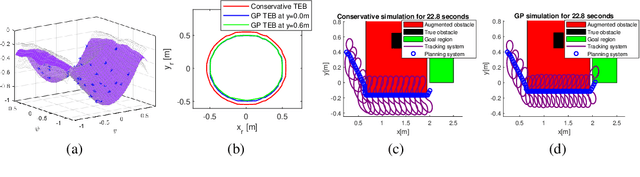
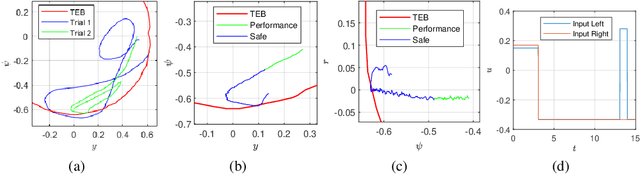
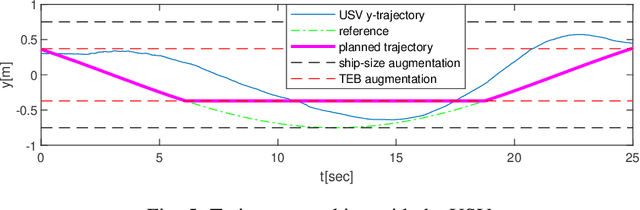
We propose a safety-guaranteed planning and control framework for unmanned surface vessels (USVs), using Gaussian processes (GPs) to learn uncertainties. The uncertainties encountered by USVs, including external disturbances and model mismatches, are potentially state-dependent, time-varying, and hard to capture with constant models. GP is a powerful learning-based tool that can be integrated with a model-based planning and control framework, which employs a Hamilton-Jacobi differential game formulation. Such a combination yields less conservative trajectories and safety-guaranteeing control strategies. We demonstrate the proposed framework in simulations and experiments on a CLEARPATH Heron USV.

MBVI: Model-Based Value Initialization for Reinforcement Learning

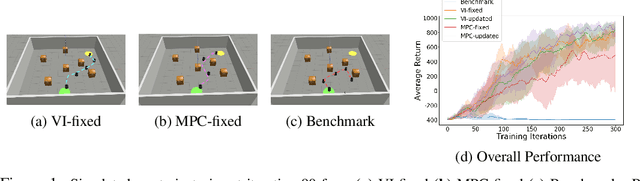
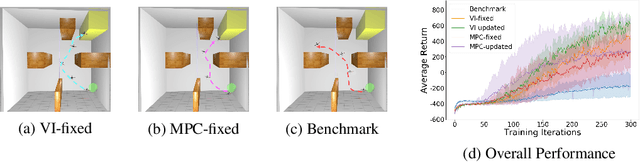
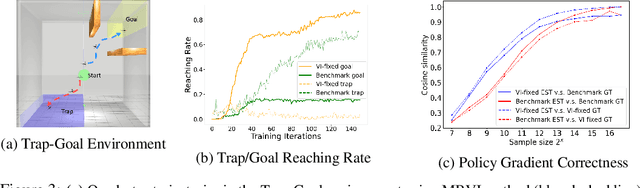
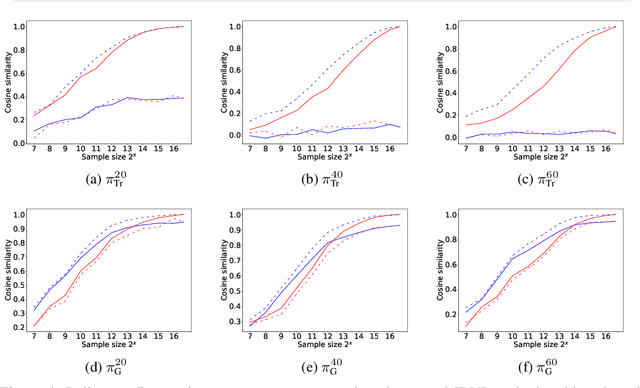
Model-free reinforcement learning (RL) is capable of learning control policies for high-dimensional, complex robotic tasks, but tends to be data inefficient. Model-based RL and optimal control have been proven to be much more data-efficient if an accurate model of the system and environment is known, but can be difficult to scale to expressive models for high-dimensional problems. In this paper, we propose a novel approach to alleviate data inefficiency of model-free RL by warm-starting the learning process using model-based solutions. We do so by initializing a high-dimensional value function via supervision from a low-dimensional value function obtained by applying model-based techniques on a low-dimensional problem featuring an approximate system model. Therefore, our approach exploits the model priors from a simplified problem space implicitly and avoids the direct use of high-dimensional, expressive models. We demonstrate our approach on two representative robotic learning tasks and observe significant improvements in performance and efficiency, and analyze our method empirically with a third task.