Non-Asymptotic Bounds for Closed-Loop Identification of Unstable Nonlinear Stochastic Systems

We consider the problem of least squares parameter estimation from single-trajectory data for discrete-time, unstable, closed-loop nonlinear stochastic systems, with linearly parameterised uncertainty. Assuming a region of the state space produces informative data, and the system is sub-exponentially unstable, we establish non-asymptotic guarantees on the estimation error at times where the state trajectory evolves in this region. If the whole state space is informative, high probability guarantees on the error hold for all times. Examples are provided where our results are useful for analysis, but existing results are not.

Stability Bounds for Learning-Based Adaptive Control of Discrete-Time Multi-Dimensional Stochastic Linear Systems with Input Constraints

We consider the problem of adaptive stabilization for discrete-time, multi-dimensional linear systems with bounded control input constraints and unbounded stochastic disturbances, where the parameters of the true system are unknown. To address this challenge, we propose a certainty-equivalent control scheme which combines online parameter estimation with saturated linear control. We establish the existence of a high probability stability bound on the closed-loop system, under additional assumptions on the system and noise processes. Finally, numerical examples are presented to illustrate our results.

Learning-Based Adaptive Control for Stochastic Linear Systems with Input Constraints

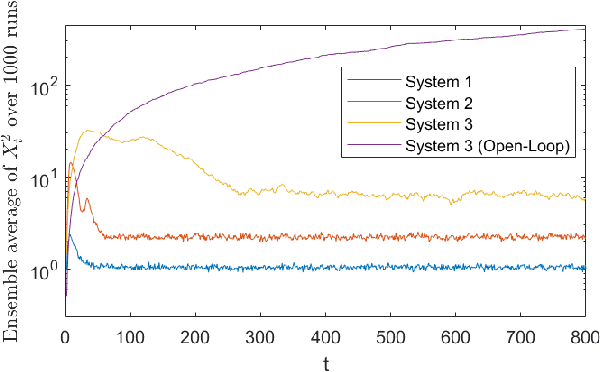
We propose a certainty-equivalence scheme for adaptive control of scalar linear systems subject to additive, i.i.d. Gaussian disturbances and bounded control input constraints, without requiring prior knowledge of the bounds of the system parameters, nor the control direction. Assuming that the system is at-worst marginally stable, mean square boundedness of the closed-loop system states is proven. Lastly, numerical examples are presented to illustrate our results.