Online Prediction of Stochastic Sequences with High Probability Regret Bounds

We revisit the classical problem of universal prediction of stochastic sequences with a finite time horizon $T$ known to the learner. The question we investigate is whether it is possible to derive vanishing regret bounds that hold with high probability, complementing existing bounds from the literature that hold in expectation. We propose such high-probability bounds which have a very similar form as the prior expectation bounds. For the case of universal prediction of a stochastic process over a countable alphabet, our bound states a convergence rate of $\mathcal{O}(T^{-1/2} δ^{-1/2})$ with probability as least $1-δ$ compared to prior known in-expectation bounds of the order $\mathcal{O}(T^{-1/2})$. We also propose an impossibility result which proves that it is not possible to improve the exponent of $δ$ in a bound of the same form without making additional assumptions.

An Asynchronous Decentralised Optimisation Algorithm for Nonconvex Problems

In this paper, we consider nonconvex decentralised optimisation and learning over a network of distributed agents. We develop an ADMM algorithm based on the Randomised Block Coordinate Douglas-Rachford splitting method which enables agents in the network to distributedly and asynchronously compute a set of first-order stationary solutions of the problem. To the best of our knowledge, this is the first decentralised and asynchronous algorithm for solving nonconvex optimisation problems with convergence proof. The numerical examples demonstrate the efficiency of the proposed algorithm for distributed Phase Retrieval and sparse Principal Component Analysis problems.

Emergence of Computational Structure in a Neural Network Physics Simulator

Neural networks often have identifiable computational structures - components of the network which perform an interpretable algorithm or task - but the mechanisms by which these emerge and the best methods for detecting these structures are not well understood. In this paper we investigate the emergence of computational structure in a transformer-like model trained to simulate the physics of a particle system, where the transformer's attention mechanism is used to transfer information between particles. We show that (a) structures emerge in the attention heads of the transformer which learn to detect particle collisions, (b) the emergence of these structures is associated to degenerate geometry in the loss landscape, and (c) the dynamics of this emergence follows a power law. This suggests that these components are governed by a degenerate "effective potential". These results have implications for the convergence time of computational structure within neural networks and suggest that the emergence of computational structure can be detected by studying the dynamics of network components.

Pulse Processing -- Overview and Challenges

The detection of irregularly spaced pulses of non-negligible width is a fascinating yet under-explored topic in signal processing. It sits adjacent to other core topics such as radar and symbol detection yet has its own distinctive challenges. Even modern techniques such as compressed sensing perform worse than may be expected on pulse processing problems. Real-world applications include nuclear spectroscopy, flow cytometry, seismic signal processing and neural spike sorting, and these in turn have applications to environmental radiation monitoring, surveying, diagnostic medicine, industrial imaging, biomedical imaging, top-down proteomics, and security screening, to name just a few. This overview paper endeavours to position the pulse processing problem in the context of signal processing. It also describes some current challenges in the field.

Recursive Filters as Linear Time-Invariant Systems

Recursive filters are treated as linear time-invariant (LTI) systems but they are not: uninitialised, they have an infinite number of outputs for any given input, while if initialised, they are not time-invariant. This short tutorial article explains how and why they can be treated as LTI systems, thereby allowing tools such as Fourier analysis to be applied. It also explains the origin of the z-transform, why the region of convergence is important, and why the z-transform fails to find an infinite number of solutions.

On the tightness of information-theoretic bounds on generalization error of learning algorithms

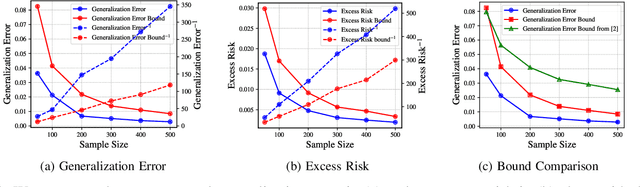
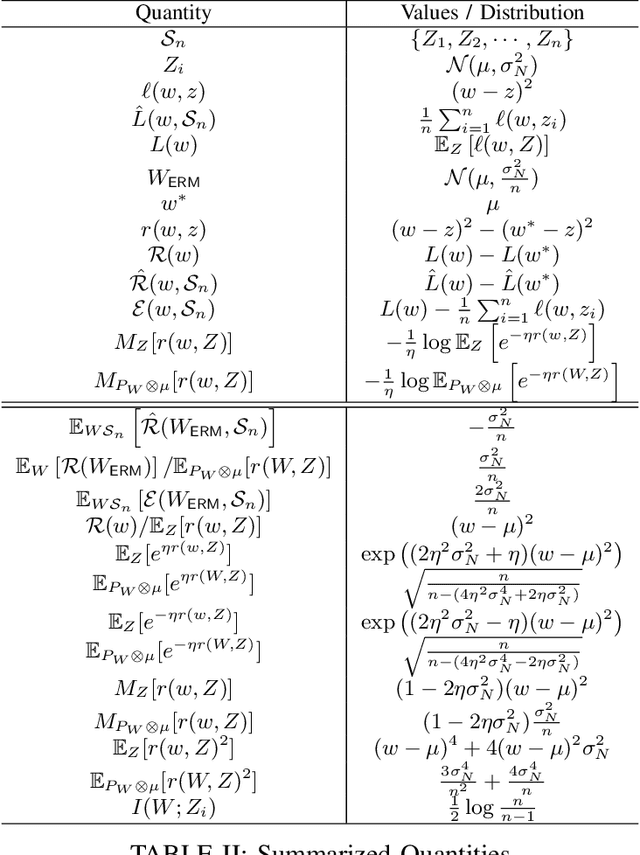
A recent line of works, initiated by Russo and Xu, has shown that the generalization error of a learning algorithm can be upper bounded by information measures. In most of the relevant works, the convergence rate of the expected generalization error is in the form of $O(\sqrt{\lambda/n})$ where $\lambda$ is some information-theoretic quantities such as the mutual information or conditional mutual information between the data and the learned hypothesis. However, such a learning rate is typically considered to be ``slow", compared to a ``fast rate" of $O(\lambda/n)$ in many learning scenarios. In this work, we first show that the square root does not necessarily imply a slow rate, and a fast rate result can still be obtained using this bound under appropriate assumptions. Furthermore, we identify the critical conditions needed for the fast rate generalization error, which we call the $(\eta,c)$-central condition. Under this condition, we give information-theoretic bounds on the generalization error and excess risk, with a fast convergence rate for specific learning algorithms such as empirical risk minimization and its regularized version. Finally, several analytical examples are given to show the effectiveness of the bounds.

An Information-Theoretic Analysis for Transfer Learning: Error Bounds and Applications

Transfer learning, or domain adaptation, is concerned with machine learning problems in which training and testing data come from possibly different probability distributions. In this work, we give an information-theoretic analysis on the generalization error and excess risk of transfer learning algorithms, following a line of work initiated by Russo and Xu. Our results suggest, perhaps as expected, that the Kullback-Leibler (KL) divergence $D(\mu||\mu')$ plays an important role in the characterizations where $\mu$ and $\mu'$ denote the distribution of the training data and the testing test, respectively. Specifically, we provide generalization error upper bounds for the empirical risk minimization (ERM) algorithm where data from both distributions are available in the training phase. We further apply the analysis to approximated ERM methods such as the Gibbs algorithm and the stochastic gradient descent method. We then generalize the mutual information bound with $\phi$-divergence and Wasserstein distance. These generalizations lead to tighter bounds and can handle the case when $\mu$ is not absolutely continuous with respect to $\mu'$. Furthermore, we apply a new set of techniques to obtain an alternative upper bound which gives a fast (and optimal) learning rate for some learning problems. Finally, inspired by the derived bounds, we propose the InfoBoost algorithm in which the importance weights for source and target data are adjusted adaptively in accordance to information measures. The empirical results show the effectiveness of the proposed algorithm.

Fast Rate Generalization Error Bounds: Variations on a Theme

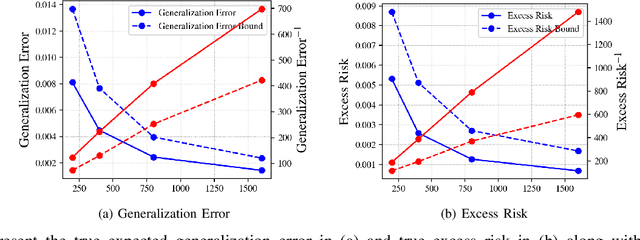
A recent line of works, initiated by Russo and Xu, has shown that the generalization error of a learning algorithm can be upper bounded by information measures. In most of the relevant works, the convergence rate of the expected generalization error is in the form of O(sqrt{lambda/n}) where lambda is some information-theoretic quantities such as the mutual information between the data sample and the learned hypothesis. However, such a learning rate is typically considered to be "slow", compared to a "fast rate" of O(1/n) in many learning scenarios. In this work, we first show that the square root does not necessarily imply a slow rate, and a fast rate (O(1/n)) result can still be obtained using this bound under appropriate assumptions. Furthermore, we identify the key conditions needed for the fast rate generalization error, which we call the (eta,c)-central condition. Under this condition, we give information-theoretic bounds on the generalization error and excess risk, with a convergence rate of O(\lambda/{n}) for specific learning algorithms such as empirical risk minimization. Finally, analytical examples are given to show the effectiveness of the bounds.

On Causality in Domain Adaptation and Semi-Supervised Learning: an Information-Theoretic Analysis

The establishment of the link between causality and unsupervised domain adaptation (UDA)/semi-supervised learning (SSL) has led to methodological advances in these learning problems in recent years. However, a formal theory that explains the role of causality in the generalization performance of UDA/SSL is still lacking. In this paper, we consider the UDA/SSL setting where we access m labeled source data and n unlabeled target data as training instances under a parametric probabilistic model. We study the learning performance (e.g., excess risk) of prediction in the target domain. Specifically, we distinguish two scenarios: the learning problem is called causal learning if the feature is the cause and the label is the effect, and is called anti-causal learning otherwise. We show that in causal learning, the excess risk depends on the size of the source sample at a rate of O(1/m) only if the labelling distribution between the source and target domains remains unchanged. In anti-causal learning, we show that the unlabeled data dominate the performance at a rate of typically O(1/n). Our analysis is based on the notion of potential outcome random variables and information theory. These results bring out the relationship between the data sample size and the hardness of the learning problem with different causal mechanisms.

On Orthogonal Approximate Message Passing

Approximate Message Passing (AMP) is an efficient iterative parameter-estimation technique for certain high-dimensional linear systems with non-Gaussian distributions, such as sparse systems. In AMP, a so-called Onsager term is added to keep estimation errors approximately Gaussian. Orthogonal AMP (OAMP) does not require this Onsager term, relying instead on an orthogonalization procedure to keep the current errors uncorrelated with (i.e., orthogonal to) past errors. In this paper, we show that the orthogonality in OAMP ensures that errors are "asymptotically independently and identically distributed Gaussian" (AIIDG). This AIIDG property, which is essential for the attractive performance of OAMP, holds for separable functions. We present a procedure to realize the required orthogonality for OAMP through Gram-Schmidt orthogonalization (GSO). We show that expectation propagation (EP), AMP, OAMP and some other algorithms can be unified under this orthogonality framework. The simplicity and generality of OAMP provide efficient solutions for estimation problems beyond the classical linear models; related applications will be discussed in a companion paper where new algorithms are developed for problems with multiple constraints and multiple measurement variables.