Fast Rate Generalization Error Bounds: Variations on a Theme
Paper and Code
May 13, 2022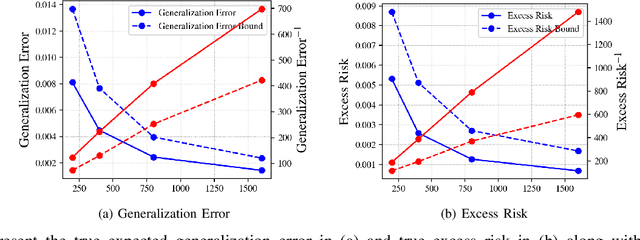


A recent line of works, initiated by Russo and Xu, has shown that the generalization error of a learning algorithm can be upper bounded by information measures. In most of the relevant works, the convergence rate of the expected generalization error is in the form of O(sqrt{lambda/n}) where lambda is some information-theoretic quantities such as the mutual information between the data sample and the learned hypothesis. However, such a learning rate is typically considered to be "slow", compared to a "fast rate" of O(1/n) in many learning scenarios. In this work, we first show that the square root does not necessarily imply a slow rate, and a fast rate (O(1/n)) result can still be obtained using this bound under appropriate assumptions. Furthermore, we identify the key conditions needed for the fast rate generalization error, which we call the (eta,c)-central condition. Under this condition, we give information-theoretic bounds on the generalization error and excess risk, with a convergence rate of O(\lambda/{n}) for specific learning algorithms such as empirical risk minimization. Finally, analytical examples are given to show the effectiveness of the bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge