Dynamical Label Augmentation and Calibration for Noisy Electronic Health Records

Medical research, particularly in predicting patient outcomes, heavily relies on medical time series data extracted from Electronic Health Records (EHR), which provide extensive information on patient histories. Despite rigorous examination, labeling errors are inevitable and can significantly impede accurate predictions of patient outcome. To address this challenge, we propose an \textbf{A}ttention-based Learning Framework with Dynamic \textbf{C}alibration and Augmentation for \textbf{T}ime series Noisy \textbf{L}abel \textbf{L}earning (ACTLL). This framework leverages a two-component Beta mixture model to identify the certain and uncertain sets of instances based on the fitness distribution of each class, and it captures global temporal dynamics while dynamically calibrating labels from the uncertain set or augmenting confident instances from the certain set. Experimental results on large-scale EHR datasets eICU and MIMIC-IV-ED, and several benchmark datasets from the UCR and UEA repositories, demonstrate that our model ACTLL has achieved state-of-the-art performance, especially under high noise levels.

SHIP: A Shapelet-based Approach for Interpretable Patient-Ventilator Asynchrony Detection

Patient-ventilator asynchrony (PVA) is a common and critical issue during mechanical ventilation, affecting up to 85% of patients. PVA can result in clinical complications such as discomfort, sleep disruption, and potentially more severe conditions like ventilator-induced lung injury and diaphragm dysfunction. Traditional PVA management, which relies on manual adjustments by healthcare providers, is often inadequate due to delays and errors. While various computational methods, including rule-based, statistical, and deep learning approaches, have been developed to detect PVA events, they face challenges related to dataset imbalances and lack of interpretability. In this work, we propose a shapelet-based approach SHIP for PVA detection, utilizing shapelets - discriminative subsequences in time-series data - to enhance detection accuracy and interpretability. Our method addresses dataset imbalances through shapelet-based data augmentation and constructs a shapelet pool to transform the dataset for more effective classification. The combined shapelet and statistical features are then used in a classifier to identify PVA events. Experimental results on medical datasets show that SHIP significantly improves PVA detection while providing interpretable insights into model decisions.

ShapeFormer: Shapelet Transformer for Multivariate Time Series Classification

Multivariate time series classification (MTSC) has attracted significant research attention due to its diverse real-world applications. Recently, exploiting transformers for MTSC has achieved state-of-the-art performance. However, existing methods focus on generic features, providing a comprehensive understanding of data, but they ignore class-specific features crucial for learning the representative characteristics of each class. This leads to poor performance in the case of imbalanced datasets or datasets with similar overall patterns but differing in minor class-specific details. In this paper, we propose a novel Shapelet Transformer (ShapeFormer), which comprises class-specific and generic transformer modules to capture both of these features. In the class-specific module, we introduce the discovery method to extract the discriminative subsequences of each class (i.e. shapelets) from the training set. We then propose a Shapelet Filter to learn the difference features between these shapelets and the input time series. We found that the difference feature for each shapelet contains important class-specific features, as it shows a significant distinction between its class and others. In the generic module, convolution filters are used to extract generic features that contain information to distinguish among all classes. For each module, we employ the transformer encoder to capture the correlation between their features. As a result, the combination of two transformer modules allows our model to exploit the power of both types of features, thereby enhancing the classification performance. Our experiments on 30 UEA MTSC datasets demonstrate that ShapeFormer has achieved the highest accuracy ranking compared to state-of-the-art methods. The code is available at https://github.com/xuanmay2701/shapeformer.

Survey on Leveraging Uncertainty Estimation Towards Trustworthy Deep Neural Networks: The Case of Reject Option and Post-training Processing

Although neural networks (especially deep neural networks) have achieved \textit{better-than-human} performance in many fields, their real-world deployment is still questionable due to the lack of awareness about the limitation in their knowledge. To incorporate such awareness in the machine learning model, prediction with reject option (also known as selective classification or classification with abstention) has been proposed in literature. In this paper, we present a systematic review of the prediction with the reject option in the context of various neural networks. To the best of our knowledge, this is the first study focusing on this aspect of neural networks. Moreover, we discuss different novel loss functions related to the reject option and post-training processing (if any) of network output for generating suitable measurements for knowledge awareness of the model. Finally, we address the application of the rejection option in reducing the prediction time for the real-time problems and present a comprehensive summary of the techniques related to the reject option in the context of extensive variety of neural networks. Our code is available on GitHub: \url{https://github.com/MehediHasanTutul/Reject_option}

On the tightness of information-theoretic bounds on generalization error of learning algorithms

A recent line of works, initiated by Russo and Xu, has shown that the generalization error of a learning algorithm can be upper bounded by information measures. In most of the relevant works, the convergence rate of the expected generalization error is in the form of $O(\sqrt{\lambda/n})$ where $\lambda$ is some information-theoretic quantities such as the mutual information or conditional mutual information between the data and the learned hypothesis. However, such a learning rate is typically considered to be ``slow", compared to a ``fast rate" of $O(\lambda/n)$ in many learning scenarios. In this work, we first show that the square root does not necessarily imply a slow rate, and a fast rate result can still be obtained using this bound under appropriate assumptions. Furthermore, we identify the critical conditions needed for the fast rate generalization error, which we call the $(\eta,c)$-central condition. Under this condition, we give information-theoretic bounds on the generalization error and excess risk, with a fast convergence rate for specific learning algorithms such as empirical risk minimization and its regularized version. Finally, several analytical examples are given to show the effectiveness of the bounds.

Enhancing Constraint Programming via Supervised Learning for Job Shop Scheduling

Constraint programming (CP) is an effective technique for solving constraint satisfaction and optimization problems. CP solvers typically use a variable ordering strategy to select which variable to explore first in the solving process, which has a large impact on the efficacy of the solvers. In this paper, we propose a novel variable ordering strategy based on supervised learning to solve job shop scheduling problems. We develop a classification model and a regression model to predict the optimal solution of a problem instance, and use the predicted solution to order variables for CP solvers. We show that training machine learning models is very efficient and can achieve a high accuracy. Our extensive experiments demonstrate that the learned variable ordering methods perform competitively compared to four existing methods. Finally, we show that hybridising the machine learning-based variable ordering methods with traditional domain-based methods is beneficial.

Multi-fidelity Gaussian Process for Biomanufacturing Process Modeling with Small Data

In biomanufacturing, developing an accurate model to simulate the complex dynamics of bioprocesses is an important yet challenging task. This is partially due to the uncertainty associated with bioprocesses, high data acquisition cost, and lack of data availability to learn complex relations in bioprocesses. To deal with these challenges, we propose to use a statistical machine learning approach, multi-fidelity Gaussian process, for process modelling in biomanufacturing. Gaussian process regression is a well-established technique based on probability theory which can naturally consider uncertainty in a dataset via Gaussian noise, and multi-fidelity techniques can make use of multiple sources of information with different levels of fidelity, thus suitable for bioprocess modeling with small data. We apply the multi-fidelity Gaussian process to solve two significant problems in biomanufacturing, bioreactor scale-up and knowledge transfer across cell lines, and demonstrate its efficacy on real-world datasets.

An Information-Theoretic Analysis for Transfer Learning: Error Bounds and Applications

Transfer learning, or domain adaptation, is concerned with machine learning problems in which training and testing data come from possibly different probability distributions. In this work, we give an information-theoretic analysis on the generalization error and excess risk of transfer learning algorithms, following a line of work initiated by Russo and Xu. Our results suggest, perhaps as expected, that the Kullback-Leibler (KL) divergence $D(\mu||\mu')$ plays an important role in the characterizations where $\mu$ and $\mu'$ denote the distribution of the training data and the testing test, respectively. Specifically, we provide generalization error upper bounds for the empirical risk minimization (ERM) algorithm where data from both distributions are available in the training phase. We further apply the analysis to approximated ERM methods such as the Gibbs algorithm and the stochastic gradient descent method. We then generalize the mutual information bound with $\phi$-divergence and Wasserstein distance. These generalizations lead to tighter bounds and can handle the case when $\mu$ is not absolutely continuous with respect to $\mu'$. Furthermore, we apply a new set of techniques to obtain an alternative upper bound which gives a fast (and optimal) learning rate for some learning problems. Finally, inspired by the derived bounds, we propose the InfoBoost algorithm in which the importance weights for source and target data are adjusted adaptively in accordance to information measures. The empirical results show the effectiveness of the proposed algorithm.

Fast Rate Generalization Error Bounds: Variations on a Theme

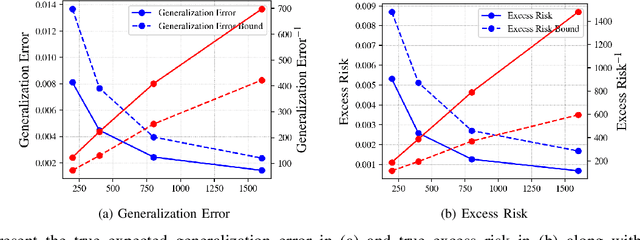
A recent line of works, initiated by Russo and Xu, has shown that the generalization error of a learning algorithm can be upper bounded by information measures. In most of the relevant works, the convergence rate of the expected generalization error is in the form of O(sqrt{lambda/n}) where lambda is some information-theoretic quantities such as the mutual information between the data sample and the learned hypothesis. However, such a learning rate is typically considered to be "slow", compared to a "fast rate" of O(1/n) in many learning scenarios. In this work, we first show that the square root does not necessarily imply a slow rate, and a fast rate (O(1/n)) result can still be obtained using this bound under appropriate assumptions. Furthermore, we identify the key conditions needed for the fast rate generalization error, which we call the (eta,c)-central condition. Under this condition, we give information-theoretic bounds on the generalization error and excess risk, with a convergence rate of O(\lambda/{n}) for specific learning algorithms such as empirical risk minimization. Finally, analytical examples are given to show the effectiveness of the bounds.

On Causality in Domain Adaptation and Semi-Supervised Learning: an Information-Theoretic Analysis

The establishment of the link between causality and unsupervised domain adaptation (UDA)/semi-supervised learning (SSL) has led to methodological advances in these learning problems in recent years. However, a formal theory that explains the role of causality in the generalization performance of UDA/SSL is still lacking. In this paper, we consider the UDA/SSL setting where we access m labeled source data and n unlabeled target data as training instances under a parametric probabilistic model. We study the learning performance (e.g., excess risk) of prediction in the target domain. Specifically, we distinguish two scenarios: the learning problem is called causal learning if the feature is the cause and the label is the effect, and is called anti-causal learning otherwise. We show that in causal learning, the excess risk depends on the size of the source sample at a rate of O(1/m) only if the labelling distribution between the source and target domains remains unchanged. In anti-causal learning, we show that the unlabeled data dominate the performance at a rate of typically O(1/n). Our analysis is based on the notion of potential outcome random variables and information theory. These results bring out the relationship between the data sample size and the hardness of the learning problem with different causal mechanisms.