Enhancing Constraint Programming via Supervised Learning for Job Shop Scheduling

Constraint programming (CP) is an effective technique for solving constraint satisfaction and optimization problems. CP solvers typically use a variable ordering strategy to select which variable to explore first in the solving process, which has a large impact on the efficacy of the solvers. In this paper, we propose a novel variable ordering strategy based on supervised learning to solve job shop scheduling problems. We develop a classification model and a regression model to predict the optimal solution of a problem instance, and use the predicted solution to order variables for CP solvers. We show that training machine learning models is very efficient and can achieve a high accuracy. Our extensive experiments demonstrate that the learned variable ordering methods perform competitively compared to four existing methods. Finally, we show that hybridising the machine learning-based variable ordering methods with traditional domain-based methods is beneficial.

An Efficient Merge Search Matheuristic for Maximising the Net Present Value of Project Schedules

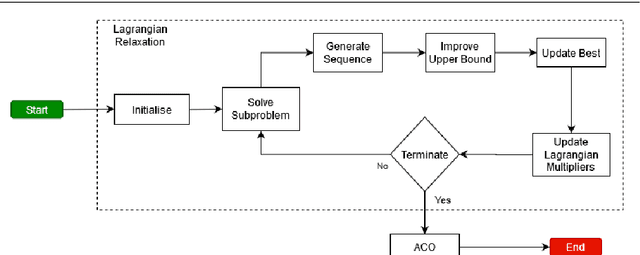
Resource constrained project scheduling is an important combinatorial optimisation problem with many practical applications. With complex requirements such as precedence constraints, limited resources, and finance-based objectives, finding optimal solutions for large problem instances is very challenging even with well-customised meta-heuristics and matheuristics. To address this challenge, we propose a new math-heuristic algorithm based on Merge Search and parallel computing to solve the resource constrained project scheduling with the aim of maximising the net present value. This paper presents a novel matheuristic framework designed for resource constrained project scheduling, Merge search, which is a variable partitioning and merging mechanism to formulate restricted mixed integer programs with the aim of improving an existing pool of solutions. The solution pool is obtained via a customised parallel ant colony optimisation algorithm, which is also capable of generating high quality solutions on its own. The experimental results show that the proposed method outperforms the current state-of-the-art algorithms on known benchmark problem instances. Further analyses also demonstrate that the proposed algorithm is substantially more efficient compared to its counterparts in respect to its convergence properties when considering multiple cores.

Instance Space Analysis for the Car Sequencing Problem

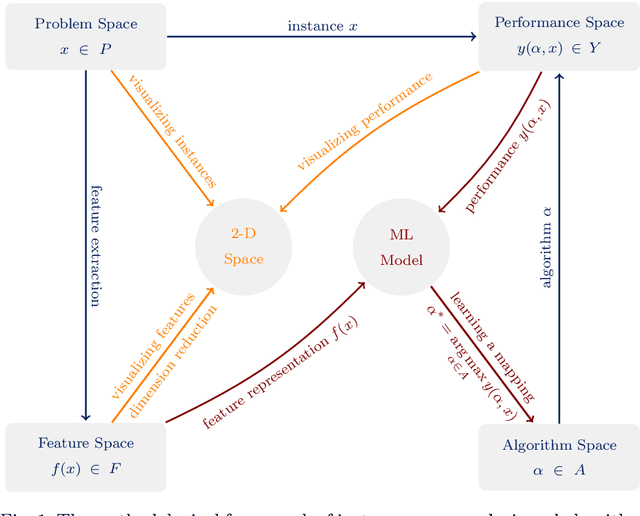
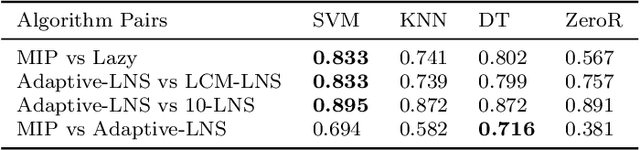
In this paper, we investigate an important research question in the car sequencing problem, that is, what characteristics make an instance hard to solve? To do so, we carry out an Instance Space Analysis for the car sequencing problem, by extracting a vector of problem features to characterize an instance and projecting feature vectors onto a two-dimensional space using principal component analysis. The resulting two dimensional visualizations provide insights into both the characteristics of the instances used for testing and to compare how these affect different optimisation algorithms. This guides us in constructing a new set of benchmark instances with a range of instance properties. These are shown to be both more diverse than the previous benchmarks and include many hard to solve instances. We systematically compare the performance of six algorithms for solving the car sequencing problem. The methods tested include three existing algorithms from the literature and three new ones. Importantly, we build machine learning models to identify the niche in the instance space that an algorithm is expected to perform well on. Our results show that the new algorithms are state-of-the-art. This analysis helps to understand problem hardness and select an appropriate algorithm for solving a given car sequencing problem instance.

Boosting Ant Colony Optimization via Solution Prediction and Machine Learning

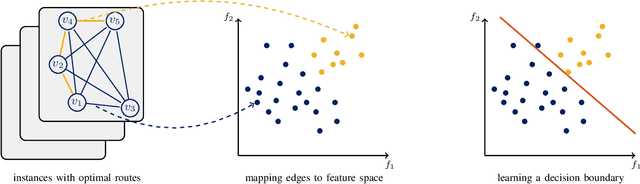
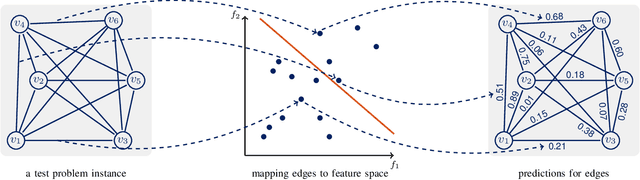
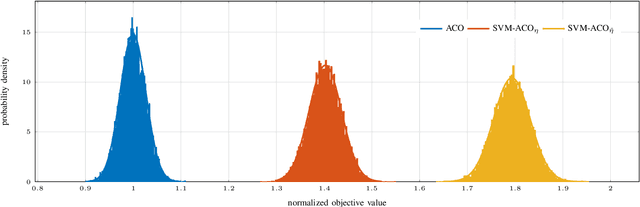
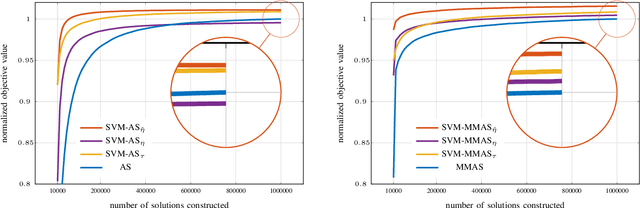
This paper introduces an enhanced meta-heuristic (ML-ACO) that combines machine learning (ML) and ant colony optimization (ACO) to solve combinatorial optimization problems. To illustrate the underlying mechanism of our enhanced algorithm, we start by describing a test problem -- the orienteering problem -- used to demonstrate the efficacy of ML-ACO. In this problem, the objective is to find a route that visits a subset of vertices in a graph within a time budget to maximize the collected score. In the first phase of our ML-ACO algorithm, an ML model is trained using a set of small problem instances where the optimal solution is known. Specifically, classification models are used to classify an edge as being part of the optimal route, or not, using problem-specific features and statistical measures. We have tested several classification models including graph neural networks, logistic regression and support vector machines. The trained model is then used to predict the probability that an edge in the graph of a test problem instance belongs to the corresponding optimal route. In the second phase, we incorporate the predicted probabilities into the ACO component of our algorithm. Here, the probability values bias sampling towards favoring those predicted high-quality edges when constructing feasible routes. We empirically show that ML-ACO generates results that are significantly better than the standard ACO algorithm, especially when the computational budget is limited. Furthermore, we show our algorithm is robust in the sense that (a) its overall performance is not sensitive to any particular classification model, and (b) it generalizes well to large and real-world problem instances. Our approach integrating ML with a meta-heuristic is generic and can be applied to a wide range of combinatorial optimization problems.