Yunzhuang Shen
Adaptive Stabilization Based on Machine Learning for Column Generation
May 18, 2024



Abstract:Column generation (CG) is a well-established method for solving large-scale linear programs. It involves iteratively optimizing a subproblem containing a subset of columns and using its dual solution to generate new columns with negative reduced costs. This process continues until the dual values converge to the optimal dual solution to the original problem. A natural phenomenon in CG is the heavy oscillation of the dual values during iterations, which can lead to a substantial slowdown in the convergence rate. Stabilization techniques are devised to accelerate the convergence of dual values by using information beyond the state of the current subproblem. However, there remains a significant gap in obtaining more accurate dual values at an earlier stage. To further narrow this gap, this paper introduces a novel approach consisting of 1) a machine learning approach for accurate prediction of optimal dual solutions and 2) an adaptive stabilization technique that effectively capitalizes on accurate predictions. On the graph coloring problem, we show that our method achieves a significantly improved convergence rate compared to traditional methods.
Enhancing Column Generation by a Machine-Learning-Based Pricing Heuristic for Graph Coloring
Dec 08, 2021


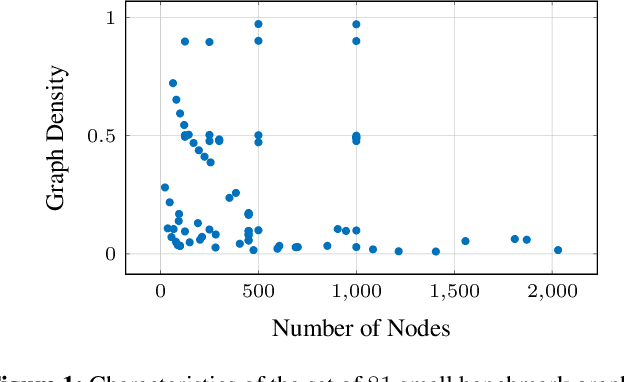
Abstract:Column Generation (CG) is an effective method for solving large-scale optimization problems. CG starts by solving a sub-problem with a subset of columns (i.e., variables) and gradually includes new columns that can improve the solution of the current subproblem. The new columns are generated as needed by repeatedly solving a pricing problem, which is often NP-hard and is a bottleneck of the CG approach. To tackle this, we propose a Machine-Learning-based Pricing Heuristic (MLPH)that can generate many high-quality columns efficiently. In each iteration of CG, our MLPH leverages an ML model to predict the optimal solution of the pricing problem, which is then used to guide a sampling method to efficiently generate multiple high-quality columns. Using the graph coloring problem, we empirically show that MLPH significantly enhancesCG as compared to six state-of-the-art methods, and the improvement in CG can lead to substantially better performance of the branch-and-price exact method.
Learning Primal Heuristics for Mixed Integer Programs
Jul 02, 2021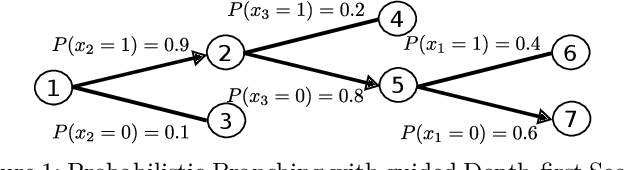
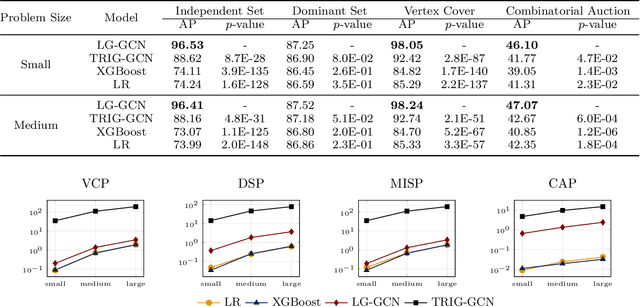
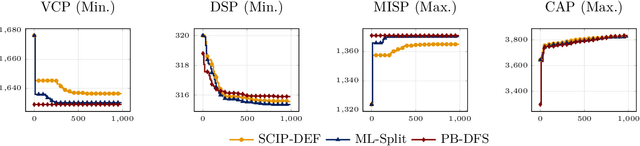
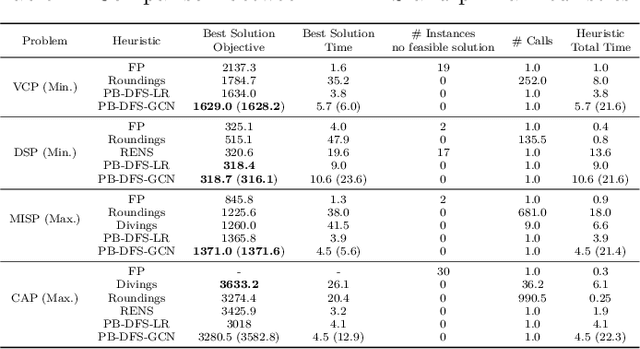
Abstract:This paper proposes a novel primal heuristic for Mixed Integer Programs, by employing machine learning techniques. Mixed Integer Programming is a general technique for formulating combinatorial optimization problems. Inside a solver, primal heuristics play a critical role in finding good feasible solutions that enable one to tighten the duality gap from the outset of the Branch-and-Bound algorithm (B&B), greatly improving its performance by pruning the B&B tree aggressively. In this paper, we investigate whether effective primal heuristics can be automatically learned via machine learning. We propose a new method to represent an optimization problem as a graph, and train a Graph Convolutional Network on solved problem instances with known optimal solutions. This in turn can predict the values of decision variables in the optimal solution for an unseen problem instance of a similar type. The prediction of variable solutions is then leveraged by a novel configuration of the B&B method, Probabilistic Branching with guided Depth-first Search (PB-DFS) approach, aiming to find (near-)optimal solutions quickly. The experimental results show that this new heuristic can find better primal solutions at a much earlier stage of the solving process, compared to other state-of-the-art primal heuristics.
Boosting Ant Colony Optimization via Solution Prediction and Machine Learning
Jul 29, 2020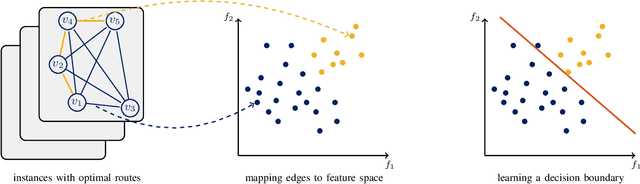
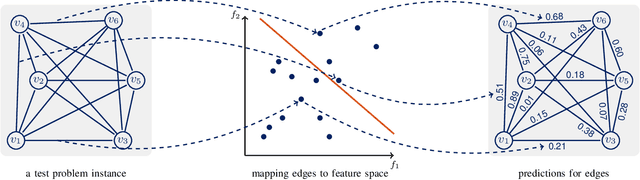
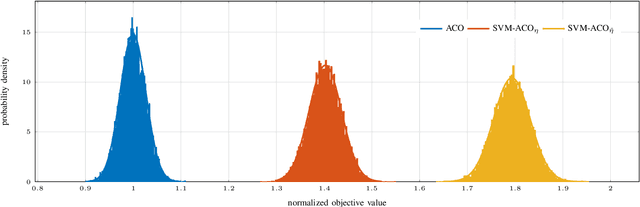
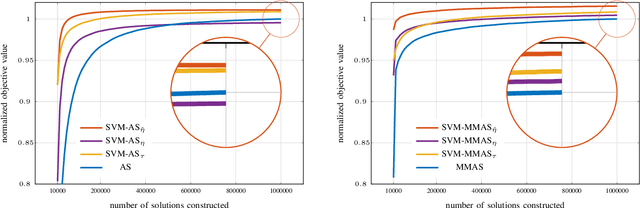
Abstract:This paper introduces an enhanced meta-heuristic (ML-ACO) that combines machine learning (ML) and ant colony optimization (ACO) to solve combinatorial optimization problems. To illustrate the underlying mechanism of our enhanced algorithm, we start by describing a test problem -- the orienteering problem -- used to demonstrate the efficacy of ML-ACO. In this problem, the objective is to find a route that visits a subset of vertices in a graph within a time budget to maximize the collected score. In the first phase of our ML-ACO algorithm, an ML model is trained using a set of small problem instances where the optimal solution is known. Specifically, classification models are used to classify an edge as being part of the optimal route, or not, using problem-specific features and statistical measures. We have tested several classification models including graph neural networks, logistic regression and support vector machines. The trained model is then used to predict the probability that an edge in the graph of a test problem instance belongs to the corresponding optimal route. In the second phase, we incorporate the predicted probabilities into the ACO component of our algorithm. Here, the probability values bias sampling towards favoring those predicted high-quality edges when constructing feasible routes. We empirically show that ML-ACO generates results that are significantly better than the standard ACO algorithm, especially when the computational budget is limited. Furthermore, we show our algorithm is robust in the sense that (a) its overall performance is not sensitive to any particular classification model, and (b) it generalizes well to large and real-world problem instances. Our approach integrating ML with a meta-heuristic is generic and can be applied to a wide range of combinatorial optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge