Adaptive Stabilization Based on Machine Learning for Column Generation

Column generation (CG) is a well-established method for solving large-scale linear programs. It involves iteratively optimizing a subproblem containing a subset of columns and using its dual solution to generate new columns with negative reduced costs. This process continues until the dual values converge to the optimal dual solution to the original problem. A natural phenomenon in CG is the heavy oscillation of the dual values during iterations, which can lead to a substantial slowdown in the convergence rate. Stabilization techniques are devised to accelerate the convergence of dual values by using information beyond the state of the current subproblem. However, there remains a significant gap in obtaining more accurate dual values at an earlier stage. To further narrow this gap, this paper introduces a novel approach consisting of 1) a machine learning approach for accurate prediction of optimal dual solutions and 2) an adaptive stabilization technique that effectively capitalizes on accurate predictions. On the graph coloring problem, we show that our method achieves a significantly improved convergence rate compared to traditional methods.

Enhancing Column Generation by a Machine-Learning-Based Pricing Heuristic for Graph Coloring

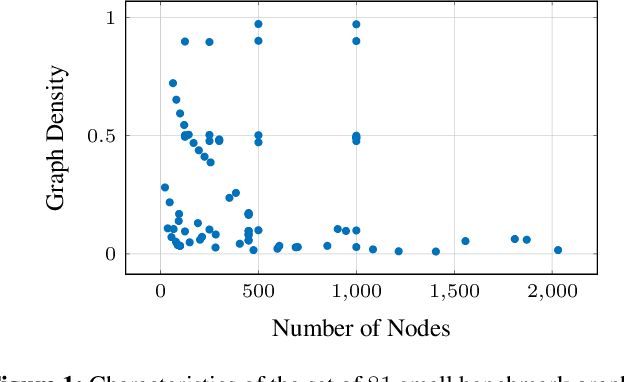
Column Generation (CG) is an effective method for solving large-scale optimization problems. CG starts by solving a sub-problem with a subset of columns (i.e., variables) and gradually includes new columns that can improve the solution of the current subproblem. The new columns are generated as needed by repeatedly solving a pricing problem, which is often NP-hard and is a bottleneck of the CG approach. To tackle this, we propose a Machine-Learning-based Pricing Heuristic (MLPH)that can generate many high-quality columns efficiently. In each iteration of CG, our MLPH leverages an ML model to predict the optimal solution of the pricing problem, which is then used to guide a sampling method to efficiently generate multiple high-quality columns. Using the graph coloring problem, we empirically show that MLPH significantly enhancesCG as compared to six state-of-the-art methods, and the improvement in CG can lead to substantially better performance of the branch-and-price exact method.

Learning Primal Heuristics for Mixed Integer Programs

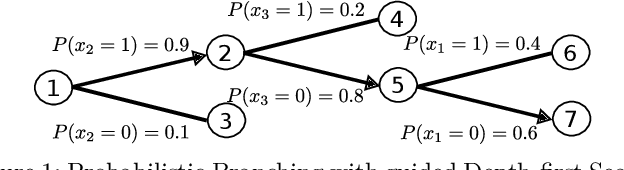
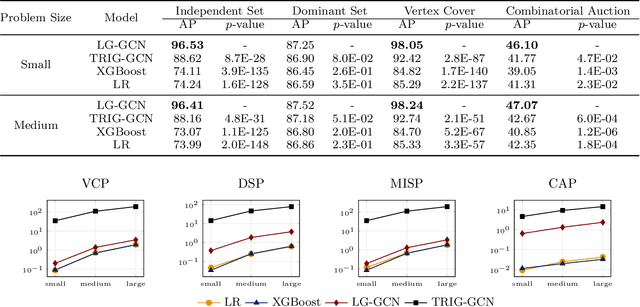
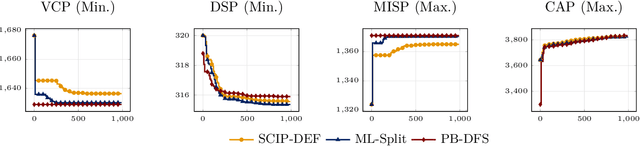
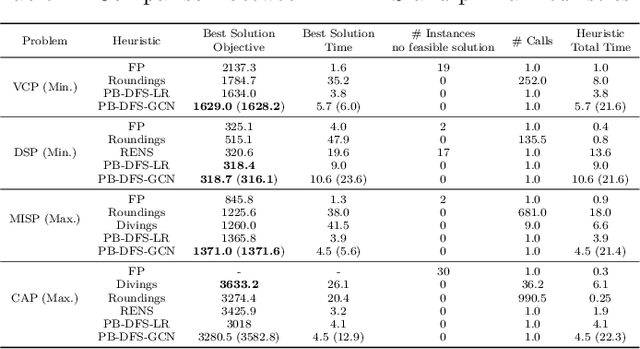
This paper proposes a novel primal heuristic for Mixed Integer Programs, by employing machine learning techniques. Mixed Integer Programming is a general technique for formulating combinatorial optimization problems. Inside a solver, primal heuristics play a critical role in finding good feasible solutions that enable one to tighten the duality gap from the outset of the Branch-and-Bound algorithm (B&B), greatly improving its performance by pruning the B&B tree aggressively. In this paper, we investigate whether effective primal heuristics can be automatically learned via machine learning. We propose a new method to represent an optimization problem as a graph, and train a Graph Convolutional Network on solved problem instances with known optimal solutions. This in turn can predict the values of decision variables in the optimal solution for an unseen problem instance of a similar type. The prediction of variable solutions is then leveraged by a novel configuration of the B&B method, Probabilistic Branching with guided Depth-first Search (PB-DFS) approach, aiming to find (near-)optimal solutions quickly. The experimental results show that this new heuristic can find better primal solutions at a much earlier stage of the solving process, compared to other state-of-the-art primal heuristics.