Can LLMs Simulate L2-English Dialogue? An Information-Theoretic Analysis of L1-Dependent Biases

This study evaluates Large Language Models' (LLMs) ability to simulate non-native-like English use observed in human second language (L2) learners interfered with by their native first language (L1). In dialogue-based interviews, we prompt LLMs to mimic L2 English learners with specific L1s (e.g., Japanese, Thai, Urdu) across seven languages, comparing their outputs to real L2 learner data. Our analysis examines L1-driven linguistic biases, such as reference word usage and avoidance behaviors, using information-theoretic and distributional density measures. Results show that modern LLMs (e.g., Qwen2.5, LLAMA3.3, DeepseekV3, GPT-4o) replicate L1-dependent patterns observed in human L2 data, with distinct influences from various languages (e.g., Japanese, Korean, and Mandarin significantly affect tense agreement, and Urdu influences noun-verb collocations). Our results reveal the potential of LLMs for L2 dialogue generation and evaluation for future educational applications.

'No' Matters: Out-of-Distribution Detection in Multimodality Long Dialogue

Out-of-distribution (OOD) detection in multimodal contexts is essential for identifying deviations in combined inputs from different modalities, particularly in applications like open-domain dialogue systems or real-life dialogue interactions. This paper aims to improve the user experience that involves multi-round long dialogues by efficiently detecting OOD dialogues and images. We introduce a novel scoring framework named Dialogue Image Aligning and Enhancing Framework (DIAEF) that integrates the visual language models with the novel proposed scores that detect OOD in two key scenarios (1) mismatches between the dialogue and image input pair and (2) input pairs with previously unseen labels. Our experimental results, derived from various benchmarks, demonstrate that integrating image and multi-round dialogue OOD detection is more effective with previously unseen labels than using either modality independently. In the presence of mismatched pairs, our proposed score effectively identifies these mismatches and demonstrates strong robustness in long dialogues. This approach enhances domain-aware, adaptive conversational agents and establishes baselines for future studies.

CNIMA: A Universal Evaluation Framework and Automated Approach for Assessing Second Language Dialogues

We develop CNIMA (Chinese Non-Native Interactivity Measurement and Automation), a Chinese-as-a-second-language labelled dataset with 10K dialogues. We annotate CNIMA using an evaluation framework -- originally introduced for English-as-a-second-language dialogues -- that assesses micro-level features (e.g.\ backchannels) and macro-level interactivity labels (e.g.\ topic management) and test the framework's transferability from English to Chinese. We found the framework robust across languages and revealed universal and language-specific relationships between micro-level and macro-level features. Next, we propose an approach to automate the evaluation and find strong performance, creating a new tool for automated second language assessment. Our system can be adapted to other languages easily as it uses large language models and as such does not require large-scale annotated training data.

On the tightness of information-theoretic bounds on generalization error of learning algorithms

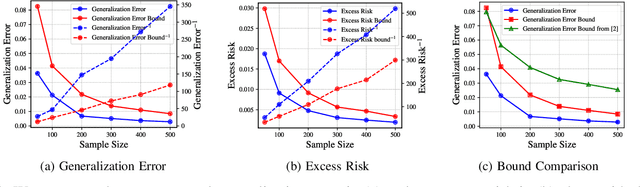
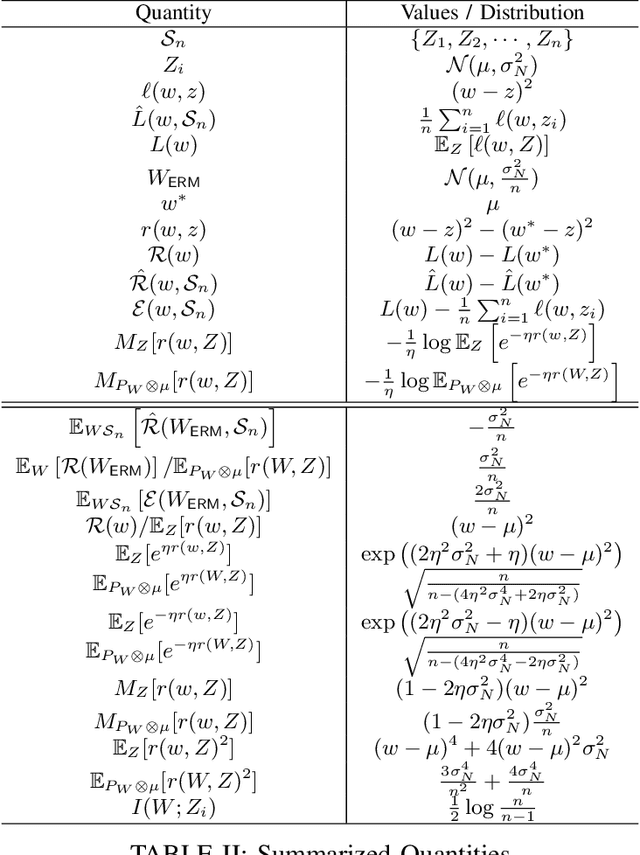
A recent line of works, initiated by Russo and Xu, has shown that the generalization error of a learning algorithm can be upper bounded by information measures. In most of the relevant works, the convergence rate of the expected generalization error is in the form of $O(\sqrt{\lambda/n})$ where $\lambda$ is some information-theoretic quantities such as the mutual information or conditional mutual information between the data and the learned hypothesis. However, such a learning rate is typically considered to be ``slow", compared to a ``fast rate" of $O(\lambda/n)$ in many learning scenarios. In this work, we first show that the square root does not necessarily imply a slow rate, and a fast rate result can still be obtained using this bound under appropriate assumptions. Furthermore, we identify the critical conditions needed for the fast rate generalization error, which we call the $(\eta,c)$-central condition. Under this condition, we give information-theoretic bounds on the generalization error and excess risk, with a fast convergence rate for specific learning algorithms such as empirical risk minimization and its regularized version. Finally, several analytical examples are given to show the effectiveness of the bounds.

On the Value of Stochastic Side Information in Online Learning

We study the effectiveness of stochastic side information in deterministic online learning scenarios. We propose a forecaster to predict a deterministic sequence where its performance is evaluated against an expert class. We assume that certain stochastic side information is available to the forecaster but not the experts. We define the minimax expected regret for evaluating the forecasters performance, for which we obtain both upper and lower bounds. Consequently, our results characterize the improvement in the regret due to the stochastic side information. Compared with the classical online learning problem with regret scales with O(\sqrt(n)), the regret can be negative when the stochastic side information is more powerful than the experts. To illustrate, we apply the proposed bounds to two concrete examples of different types of side information.

An Information-Theoretic Analysis for Transfer Learning: Error Bounds and Applications

Transfer learning, or domain adaptation, is concerned with machine learning problems in which training and testing data come from possibly different probability distributions. In this work, we give an information-theoretic analysis on the generalization error and excess risk of transfer learning algorithms, following a line of work initiated by Russo and Xu. Our results suggest, perhaps as expected, that the Kullback-Leibler (KL) divergence $D(\mu||\mu')$ plays an important role in the characterizations where $\mu$ and $\mu'$ denote the distribution of the training data and the testing test, respectively. Specifically, we provide generalization error upper bounds for the empirical risk minimization (ERM) algorithm where data from both distributions are available in the training phase. We further apply the analysis to approximated ERM methods such as the Gibbs algorithm and the stochastic gradient descent method. We then generalize the mutual information bound with $\phi$-divergence and Wasserstein distance. These generalizations lead to tighter bounds and can handle the case when $\mu$ is not absolutely continuous with respect to $\mu'$. Furthermore, we apply a new set of techniques to obtain an alternative upper bound which gives a fast (and optimal) learning rate for some learning problems. Finally, inspired by the derived bounds, we propose the InfoBoost algorithm in which the importance weights for source and target data are adjusted adaptively in accordance to information measures. The empirical results show the effectiveness of the proposed algorithm.

Fast Rate Generalization Error Bounds: Variations on a Theme

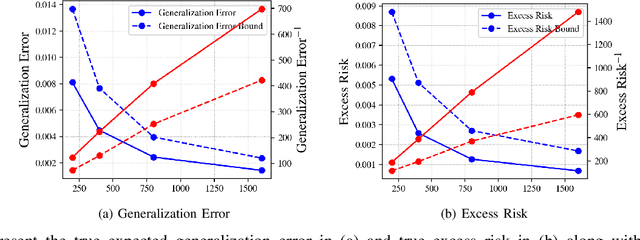
A recent line of works, initiated by Russo and Xu, has shown that the generalization error of a learning algorithm can be upper bounded by information measures. In most of the relevant works, the convergence rate of the expected generalization error is in the form of O(sqrt{lambda/n}) where lambda is some information-theoretic quantities such as the mutual information between the data sample and the learned hypothesis. However, such a learning rate is typically considered to be "slow", compared to a "fast rate" of O(1/n) in many learning scenarios. In this work, we first show that the square root does not necessarily imply a slow rate, and a fast rate (O(1/n)) result can still be obtained using this bound under appropriate assumptions. Furthermore, we identify the key conditions needed for the fast rate generalization error, which we call the (eta,c)-central condition. Under this condition, we give information-theoretic bounds on the generalization error and excess risk, with a convergence rate of O(\lambda/{n}) for specific learning algorithms such as empirical risk minimization. Finally, analytical examples are given to show the effectiveness of the bounds.

On Causality in Domain Adaptation and Semi-Supervised Learning: an Information-Theoretic Analysis

The establishment of the link between causality and unsupervised domain adaptation (UDA)/semi-supervised learning (SSL) has led to methodological advances in these learning problems in recent years. However, a formal theory that explains the role of causality in the generalization performance of UDA/SSL is still lacking. In this paper, we consider the UDA/SSL setting where we access m labeled source data and n unlabeled target data as training instances under a parametric probabilistic model. We study the learning performance (e.g., excess risk) of prediction in the target domain. Specifically, we distinguish two scenarios: the learning problem is called causal learning if the feature is the cause and the label is the effect, and is called anti-causal learning otherwise. We show that in causal learning, the excess risk depends on the size of the source sample at a rate of O(1/m) only if the labelling distribution between the source and target domains remains unchanged. In anti-causal learning, we show that the unlabeled data dominate the performance at a rate of typically O(1/n). Our analysis is based on the notion of potential outcome random variables and information theory. These results bring out the relationship between the data sample size and the hardness of the learning problem with different causal mechanisms.

A Bayesian Approach to (Online) Transfer Learning: Theory and Algorithms

Transfer learning is a machine learning paradigm where knowledge from one problem is utilized to solve a new but related problem. While conceivable that knowledge from one task could be useful for solving a related task, if not executed properly, transfer learning algorithms can impair the learning performance instead of improving it -- commonly known as negative transfer. In this paper, we study transfer learning from a Bayesian perspective, where a parametric statistical model is used. Specifically, we study three variants of transfer learning problems, instantaneous, online, and time-variant transfer learning. For each problem, we define an appropriate objective function, and provide either exact expressions or upper bounds on the learning performance using information-theoretic quantities, which allow simple and explicit characterizations when the sample size becomes large. Furthermore, examples show that the derived bounds are accurate even for small sample sizes. The obtained bounds give valuable insights into the effect of prior knowledge for transfer learning, at least with respect to our Bayesian formulation of the transfer learning problem. In particular, we formally characterize the conditions under which negative transfer occurs. Lastly, we devise two (online) transfer learning algorithms that are amenable to practical implementations, one of which does not require the parametric assumption. We demonstrate the effectiveness of our algorithms with real data sets, focusing primarily on when the source and target data have strong similarities.

Online Transfer Learning: Negative Transfer and Effect of Prior Knowledge

Transfer learning is a machine learning paradigm where the knowledge from one task is utilized to resolve the problem in a related task. On the one hand, it is conceivable that knowledge from one task could be useful for solving a related problem. On the other hand, it is also recognized that if not executed properly, transfer learning algorithms could in fact impair the learning performance instead of improving it - commonly known as "negative transfer". In this paper, we study the online transfer learning problems where the source samples are given in an offline way while the target samples arrive sequentially. We define the expected regret of the online transfer learning problem and provide upper bounds on the regret using information-theoretic quantities. We also obtain exact expressions for the bounds when the sample size becomes large. Examples show that the derived bounds are accurate even for small sample sizes. Furthermore, the obtained bounds give valuable insight on the effect of prior knowledge for transfer learning in our formulation. In particular, we formally characterize the conditions under which negative transfer occurs.