Orthogonal AMP for Problems with Multiple Measurement Vectors and/or Multiple Transforms

Approximate message passing (AMP) algorithms break a (high-dimensional) statistical problem into parts then repeatedly solve each part in turn, akin to alternating projections. A distinguishing feature is their asymptotic behaviours can be accurately predicted via their associated state evolution equations. Orthogonal AMP (OAMP) was recently developed to avoid the need for computing the so-called Onsager term in traditional AMP algorithms, providing two clear benefits: the derivation of an OAMP algorithm is both straightforward and more broadly applicable. OAMP was originally demonstrated for statistical problems with a single measurement vector and single transform. This paper extends OAMP to statistical problems with multiple measurement vectors (MMVs) and multiple transforms (MTs). We name the resulting algorithms as OAMP-MMV and OAMP-MT respectively, and their combination as augmented OAMP (A-OAMP). Whereas the extension of traditional AMP algorithms to such problems would be challenging, the orthogonal principle underpinning OAMP makes these extensions straightforward. The MMV and MT models are widely applicable to signal processing and communications. We present an example of MIMO relay system with correlated source data and signal clipping, which can be modelled as a joint MMV-MT system. While existing methods meet with difficulties in this example, OAMP offers an efficient solution with excellent performance.

Capacity Optimality of OAMP in Coded Large Unitarily Invariant Systems

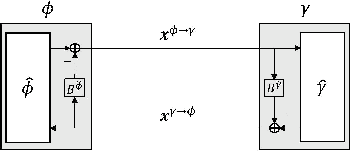
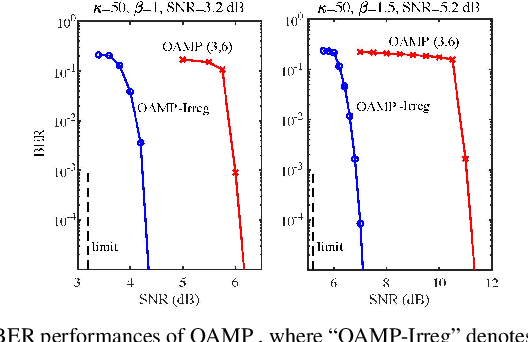
This paper investigates a large unitarily invariant system (LUIS) involving a unitarily invariant sensing matrix, an arbitrary fixed signal distribution, and forward error control (FEC) coding. Several area properties are established based on the state evolution of orthogonal approximate message passing (OAMP) in an un-coded LUIS. Under the assumptions that the state evolution for joint OAMP and FEC decoding is correct and the replica method is reliable, we analyze the achievable rate of OAMP. We prove that OAMP reaches the constrained capacity predicted by the replica method of the LUIS with an arbitrary signal distribution based on matched FEC coding. Meanwhile, we elaborate a constrained capacity-achieving coding principle for LUIS, based on which irregular low-density parity-check (LDPC) codes are optimized for binary signaling in the simulation results. We show that OAMP with the optimized codes has significant performance improvement over the un-optimized ones and the well-known Turbo linear MMSE algorithm. For quadrature phase-shift keying (QPSK) modulation, constrained capacity-approaching bit error rate (BER) performances are observed under various channel conditions.

On Orthogonal Approximate Message Passing

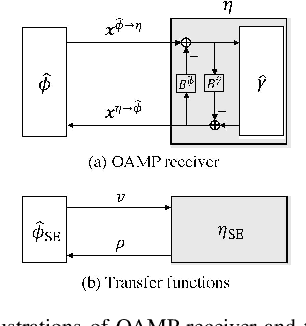
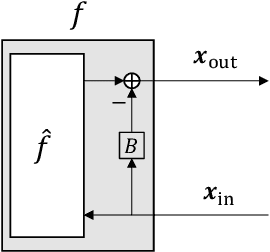
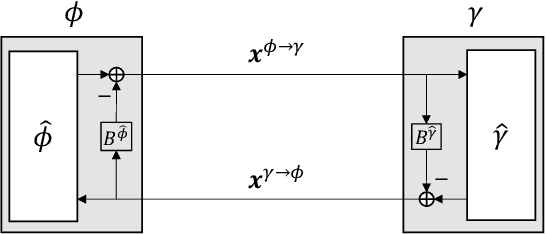
Approximate Message Passing (AMP) is an efficient iterative parameter-estimation technique for certain high-dimensional linear systems with non-Gaussian distributions, such as sparse systems. In AMP, a so-called Onsager term is added to keep estimation errors approximately Gaussian. Orthogonal AMP (OAMP) does not require this Onsager term, relying instead on an orthogonalization procedure to keep the current errors uncorrelated with (i.e., orthogonal to) past errors. In this paper, we show that the orthogonality in OAMP ensures that errors are "asymptotically independently and identically distributed Gaussian" (AIIDG). This AIIDG property, which is essential for the attractive performance of OAMP, holds for separable functions. We present a procedure to realize the required orthogonality for OAMP through Gram-Schmidt orthogonalization (GSO). We show that expectation propagation (EP), AMP, OAMP and some other algorithms can be unified under this orthogonality framework. The simplicity and generality of OAMP provide efficient solutions for estimation problems beyond the classical linear models; related applications will be discussed in a companion paper where new algorithms are developed for problems with multiple constraints and multiple measurement variables.

Capacity Optimality of OAMP: Beyond IID Sensing Matrices and Gaussian Signaling

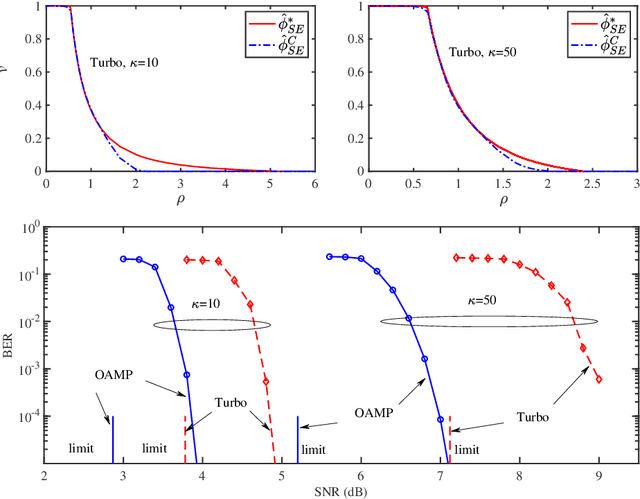
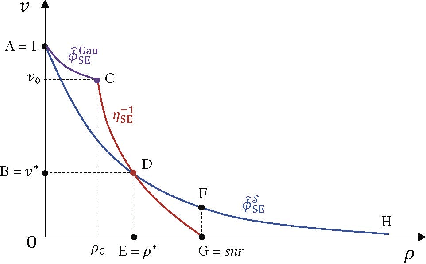
This paper studies a large unitarily invariant system (LUIS) involving a unitarily invariant sensing matrix, an arbitrary signal distribution, and forward error control (FEC) coding. We develop a universal Gram-Schmidt orthogonalization for orthogonal approximate message passing (OAMP). Numerous area properties are established based on the state evolution and minimum mean squared error (MMSE) property of OAMP in an un-coded LUIS. As a byproduct, we provide an alternative derivation for the constrained capacity of a LUIS. Under the assumption that the state evolution for OAMP is correct for the coded system, the achievable rate of OAMP is analyzed. We prove that OAMP achieves the constrained capacity of the LUIS with an arbitrary signal distribution provided that a matching condition is satisfied. Meanwhile, we elaborate a capacity-achieving coding principle for LUIS, based on which irregular low-density parity-check (LDPC) codes are optimized for binary signaling in the numerical results. We show that OAMP with the optimized codes has significant performance improvement over the un-optimized ones and the well-known Turbo linear MMSE algorithm. For quadrature phase-shift keying (QPSK) modulation, capacity-approaching bit error rate (BER) performances are observed under various channel conditions.