Emergence of Computational Structure in a Neural Network Physics Simulator

Neural networks often have identifiable computational structures - components of the network which perform an interpretable algorithm or task - but the mechanisms by which these emerge and the best methods for detecting these structures are not well understood. In this paper we investigate the emergence of computational structure in a transformer-like model trained to simulate the physics of a particle system, where the transformer's attention mechanism is used to transfer information between particles. We show that (a) structures emerge in the attention heads of the transformer which learn to detect particle collisions, (b) the emergence of these structures is associated to degenerate geometry in the loss landscape, and (c) the dynamics of this emergence follows a power law. This suggests that these components are governed by a degenerate "effective potential". These results have implications for the convergence time of computational structure within neural networks and suggest that the emergence of computational structure can be detected by studying the dynamics of network components.

PINN-Ray: A Physics-Informed Neural Network to Model Soft Robotic Fin Ray Fingers

Modelling complex deformation for soft robotics provides a guideline to understand their behaviour, leading to safe interaction with the environment. However, building a surrogate model with high accuracy and fast inference speed can be challenging for soft robotics due to the nonlinearity from complex geometry, large deformation, material nonlinearity etc. The reality gap from surrogate models also prevents their further deployment in the soft robotics domain. In this study, we proposed a physics-informed Neural Networks (PINNs) named PINN-Ray to model complex deformation for a Fin Ray soft robotic gripper, which embeds the minimum potential energy principle from elastic mechanics and additional high-fidelity experimental data into the loss function of neural network for training. This method is significant in terms of its generalisation to complex geometry and robust to data scarcity as compared to other data-driven neural networks. Furthermore, it has been extensively evaluated to model the deformation of the Fin Ray finger under external actuation. PINN-Ray demonstrates improved accuracy as compared with Finite element modelling (FEM) after applying the data assimilation scheme to treat the sim-to-real gap. Additionally, we introduced our automated framework to design, fabricate soft robotic fingers, and characterise their deformation by visual tracking, which provides a guideline for the fast prototype of soft robotics.

Efficiency and robustness in Monte Carlo sampling of 3-D geophysical inversions with Obsidian v0.1.2: Setting up for success

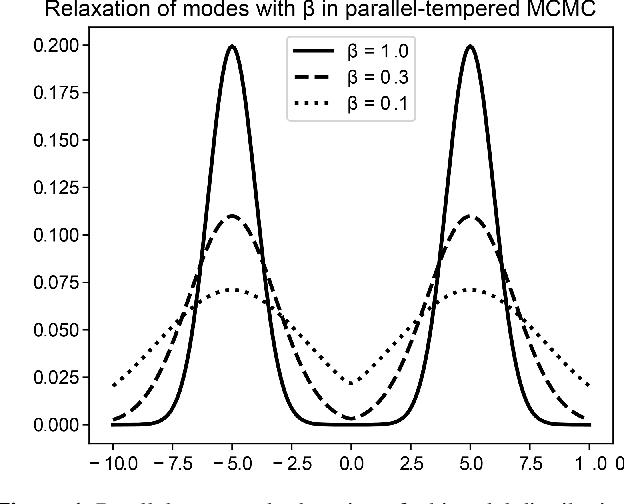
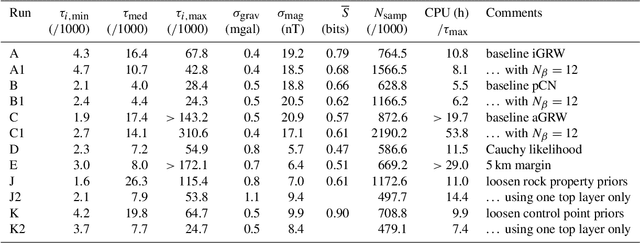
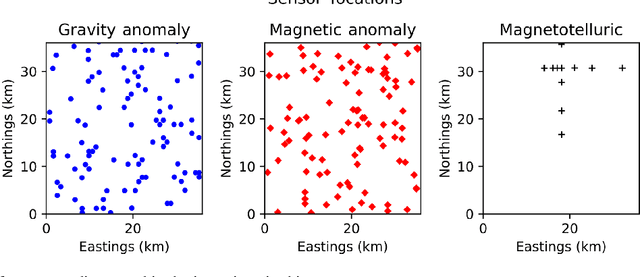
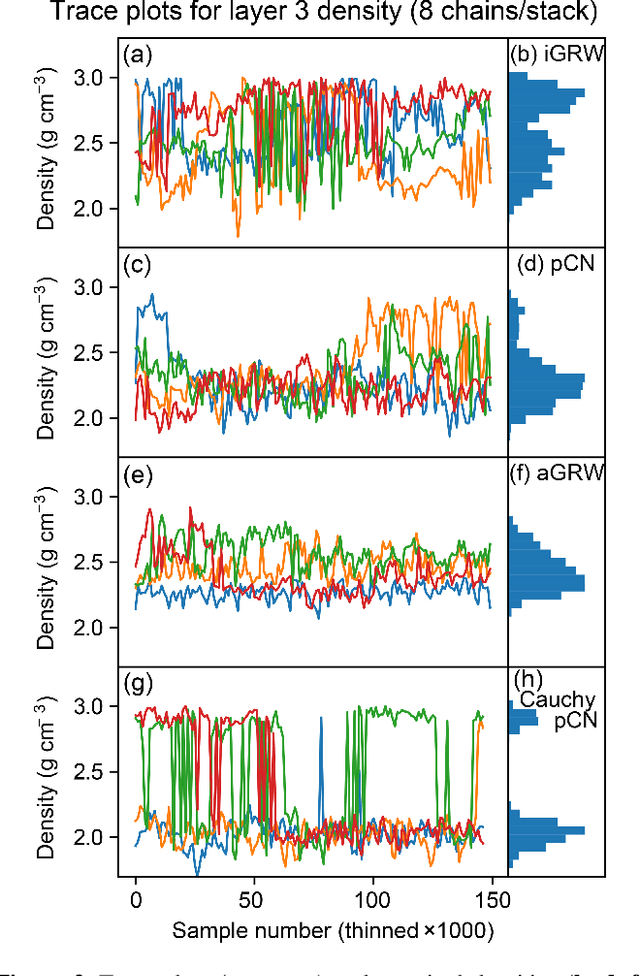
The rigorous quantification of uncertainty in geophysical inversions is a challenging problem. Inversions are often ill-posed and the likelihood surface may be multi-modal; properties of any single mode become inadequate uncertainty measures, and sampling methods become inefficient for irregular posteriors or high-dimensional parameter spaces. We explore the influences of different choices made by the practitioner on the efficiency and accuracy of Bayesian geophysical inversion methods that rely on Markov chain Monte Carlo sampling to assess uncertainty, using a multi-sensor inversion of the three-dimensional structure and composition of a region in the Cooper Basin of South Australia as a case study. The inversion is performed using an updated version of the Obsidian distributed inversion software. We find that the posterior for this inversion has complex local covariance structure, hindering the efficiency of adaptive sampling methods that adjust the proposal based on the chain history. Within the context of a parallel-tempered Markov chain Monte Carlo scheme for exploring high-dimensional multi-modal posteriors, a preconditioned Crank-Nicholson proposal outperforms more conventional forms of random walk. Aspects of the problem setup, such as priors on petrophysics or on 3-D geological structure, affect the shape and separation of posterior modes, influencing sampling performance as well as the inversion results. Use of uninformative priors on sensor noise can improve inversion results by enabling optimal weighting among multiple sensors even if noise levels are uncertain. Efficiency could be further increased by using posterior gradient information within proposals, which Obsidian does not currently support, but which could be emulated using posterior surrogates.