Sanghamitra Dutta
TabDistill: Distilling Transformers into Neural Nets for Few-Shot Tabular Classification
Nov 07, 2025Abstract:Transformer-based models have shown promising performance on tabular data compared to their classical counterparts such as neural networks and Gradient Boosted Decision Trees (GBDTs) in scenarios with limited training data. They utilize their pre-trained knowledge to adapt to new domains, achieving commendable performance with only a few training examples, also called the few-shot regime. However, the performance gain in the few-shot regime comes at the expense of significantly increased complexity and number of parameters. To circumvent this trade-off, we introduce TabDistill, a new strategy to distill the pre-trained knowledge in complex transformer-based models into simpler neural networks for effectively classifying tabular data. Our framework yields the best of both worlds: being parameter-efficient while performing well with limited training data. The distilled neural networks surpass classical baselines such as regular neural networks, XGBoost and logistic regression under equal training data, and in some cases, even the original transformer-based models that they were distilled from.
Few-Shot Knowledge Distillation of LLMs With Counterfactual Explanations
Oct 24, 2025Abstract:Knowledge distillation is a promising approach to transfer capabilities from complex teacher models to smaller, resource-efficient student models that can be deployed easily, particularly in task-aware scenarios. However, existing methods of task-aware distillation typically require substantial quantities of data which may be unavailable or expensive to obtain in many practical scenarios. In this paper, we address this challenge by introducing a novel strategy called Counterfactual-explanation-infused Distillation CoD for few-shot task-aware knowledge distillation by systematically infusing counterfactual explanations. Counterfactual explanations (CFEs) refer to inputs that can flip the output prediction of the teacher model with minimum perturbation. Our strategy CoD leverages these CFEs to precisely map the teacher's decision boundary with significantly fewer samples. We provide theoretical guarantees for motivating the role of CFEs in distillation, from both statistical and geometric perspectives. We mathematically show that CFEs can improve parameter estimation by providing more informative examples near the teacher's decision boundary. We also derive geometric insights on how CFEs effectively act as knowledge probes, helping the students mimic the teacher's decision boundaries more effectively than standard data. We perform experiments across various datasets and LLMs to show that CoD outperforms standard distillation approaches in few-shot regimes (as low as 8-512 samples). Notably, CoD only uses half of the original samples used by the baselines, paired with their corresponding CFEs and still improves performance.
Improving Consistency in Retrieval-Augmented Systems with Group Similarity Rewards
Oct 05, 2025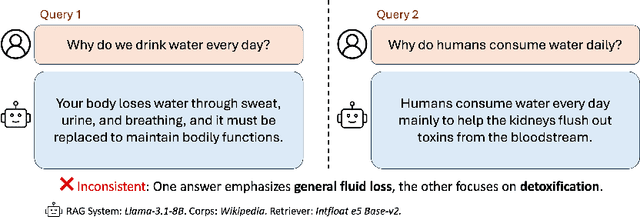
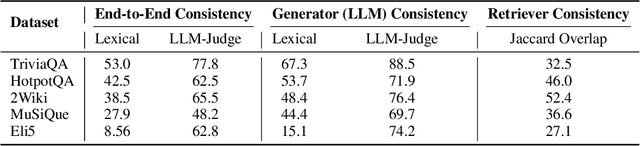
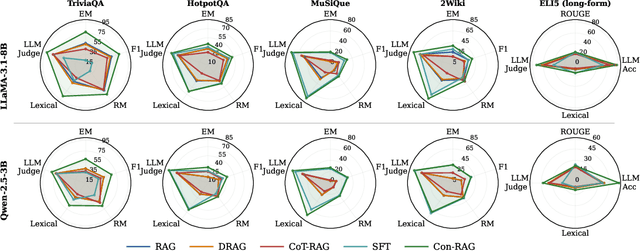
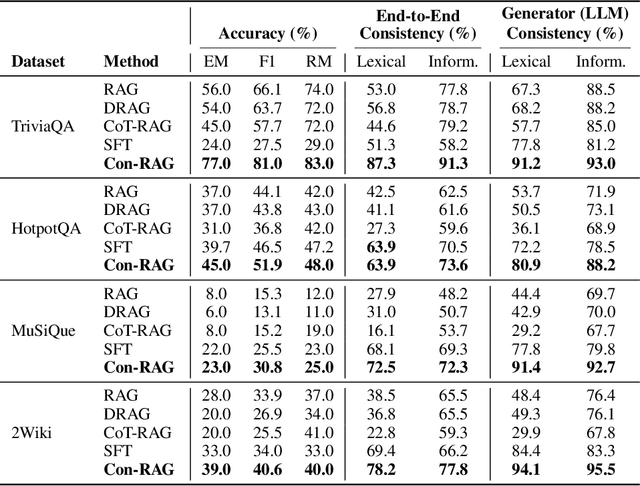
Abstract:RAG systems are increasingly deployed in high-stakes domains where users expect outputs to be consistent across semantically equivalent queries. However, existing systems often exhibit significant inconsistencies due to variability in both the retriever and generator (LLM), undermining trust and reliability. In this work, we focus on information consistency, i.e., the requirement that outputs convey the same core content across semantically equivalent inputs. We introduce a principled evaluation framework that decomposes RAG consistency into retriever-level, generator-level, and end-to-end components, helping identify inconsistency sources. To improve consistency, we propose Paraphrased Set Group Relative Policy Optimization (PS-GRPO), an RL approach that leverages multiple rollouts across paraphrased set to assign group similarity rewards. We leverage PS-GRPO to achieve Information Consistent RAG (Con-RAG), training the generator to produce consistent outputs across paraphrased queries and remain robust to retrieval-induced variability. Because exact reward computation over paraphrase sets is computationally expensive, we also introduce a scalable approximation method that retains effectiveness while enabling efficient, large-scale training. Empirical evaluations across short-form, multi-hop, and long-form QA benchmarks demonstrate that Con-RAG significantly improves both consistency and accuracy over strong baselines, even in the absence of explicit ground-truth supervision. Our work provides practical solutions for evaluating and building reliable RAG systems for safety-critical deployments.
VISION: Robust and Interpretable Code Vulnerability Detection Leveraging Counterfactual Augmentation
Aug 26, 2025Abstract:Automated detection of vulnerabilities in source code is an essential cybersecurity challenge, underpinning trust in digital systems and services. Graph Neural Networks (GNNs) have emerged as a promising approach as they can learn structural and logical code relationships in a data-driven manner. However, their performance is severely constrained by training data imbalances and label noise. GNNs often learn 'spurious' correlations from superficial code similarities, producing detectors that fail to generalize well to unseen real-world data. In this work, we propose a unified framework for robust and interpretable vulnerability detection, called VISION, to mitigate spurious correlations by systematically augmenting a counterfactual training dataset. Counterfactuals are samples with minimal semantic modifications but opposite labels. Our framework includes: (i) generating counterfactuals by prompting a Large Language Model (LLM); (ii) targeted GNN training on paired code examples with opposite labels; and (iii) graph-based interpretability to identify the crucial code statements relevant for vulnerability predictions while ignoring spurious ones. We find that VISION reduces spurious learning and enables more robust, generalizable detection, improving overall accuracy (from 51.8% to 97.8%), pairwise contrast accuracy (from 4.5% to 95.8%), and worst-group accuracy (from 0.7% to 85.5%) on the Common Weakness Enumeration (CWE)-20 vulnerability. We further demonstrate gains using proposed metrics: intra-class attribution variance, inter-class attribution distance, and node score dependency. We also release CWE-20-CFA, a benchmark of 27,556 functions (real and counterfactual) from the high-impact CWE-20 category. Finally, VISION advances transparent and trustworthy AI-based cybersecurity systems through interactive visualization for human-in-the-loop analysis.
Counterfactual Explanations for Model Ensembles Using Entropic Risk Measures
Mar 11, 2025



Abstract:Counterfactual explanations indicate the smallest change in input that can translate to a different outcome for a machine learning model. Counterfactuals have generated immense interest in high-stakes applications such as finance, education, hiring, etc. In several use-cases, the decision-making process often relies on an ensemble of models rather than just one. Despite significant research on counterfactuals for one model, the problem of generating a single counterfactual explanation for an ensemble of models has received limited interest. Each individual model might lead to a different counterfactual, whereas trying to find a counterfactual accepted by all models might significantly increase cost (effort). We propose a novel strategy to find the counterfactual for an ensemble of models using the perspective of entropic risk measure. Entropic risk is a convex risk measure that satisfies several desirable properties. We incorporate our proposed risk measure into a novel constrained optimization to generate counterfactuals for ensembles that stay valid for several models. The main significance of our measure is that it provides a knob that allows for the generation of counterfactuals that stay valid under an adjustable fraction of the models. We also show that a limiting case of our entropic-risk-based strategy yields a counterfactual valid for all models in the ensemble (worst-case min-max approach). We study the trade-off between the cost (effort) for the counterfactual and its validity for an ensemble by varying degrees of risk aversion, as determined by our risk parameter knob. We validate our performance on real-world datasets.
Demystifying the Accuracy-Interpretability Trade-Off: A Case Study of Inferring Ratings from Reviews
Mar 10, 2025Abstract:Interpretable machine learning models offer understandable reasoning behind their decision-making process, though they may not always match the performance of their black-box counterparts. This trade-off between interpretability and model performance has sparked discussions around the deployment of AI, particularly in critical applications where knowing the rationale of decision-making is essential for trust and accountability. In this study, we conduct a comparative analysis of several black-box and interpretable models, focusing on a specific NLP use case that has received limited attention: inferring ratings from reviews. Through this use case, we explore the intricate relationship between the performance and interpretability of different models. We introduce a quantitative score called Composite Interpretability (CI) to help visualize the trade-off between interpretability and performance, particularly in the case of composite models. Our results indicate that, in general, the learning performance improves as interpretability decreases, but this relationship is not strictly monotonic, and there are instances where interpretable models are more advantageous.
Private Counterfactual Retrieval With Immutable Features
Nov 15, 2024Abstract:In a classification task, counterfactual explanations provide the minimum change needed for an input to be classified into a favorable class. We consider the problem of privately retrieving the exact closest counterfactual from a database of accepted samples while enforcing that certain features of the input sample cannot be changed, i.e., they are \emph{immutable}. An applicant (user) whose feature vector is rejected by a machine learning model wants to retrieve the sample closest to them in the database without altering a private subset of their features, which constitutes the immutable set. While doing this, the user should keep their feature vector, immutable set and the resulting counterfactual index information-theoretically private from the institution. We refer to this as immutable private counterfactual retrieval (I-PCR) problem which generalizes PCR to a more practical setting. In this paper, we propose two I-PCR schemes by leveraging techniques from private information retrieval (PIR) and characterize their communication costs. Further, we quantify the information that the user learns about the database and compare it for the proposed schemes.
Quantifying Knowledge Distillation Using Partial Information Decomposition
Nov 12, 2024Abstract:Knowledge distillation provides an effective method for deploying complex machine learning models in resource-constrained environments. It typically involves training a smaller student model to emulate either the probabilistic outputs or the internal feature representations of a larger teacher model. By doing so, the student model often achieves substantially better performance on a downstream task compared to when it is trained independently. Nevertheless, the teacher's internal representations can also encode noise or additional information that may not be relevant to the downstream task. This observation motivates our primary question: What are the information-theoretic limits of knowledge transfer? To this end, we leverage a body of work in information theory called Partial Information Decomposition (PID) to quantify the distillable and distilled knowledge of a teacher's representation corresponding to a given student and a downstream task. Moreover, we demonstrate that this metric can be practically used in distillation to address challenges caused by the complexity gap between the teacher and the student representations.
Private Counterfactual Retrieval
Oct 17, 2024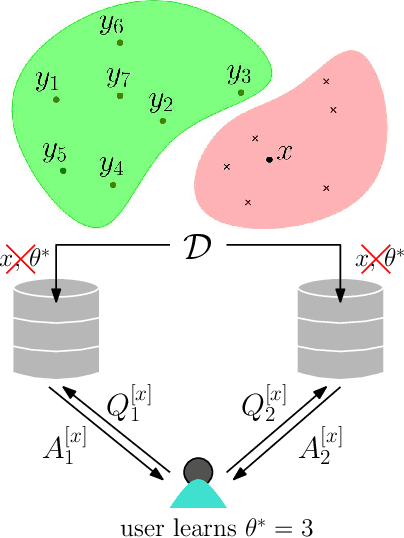

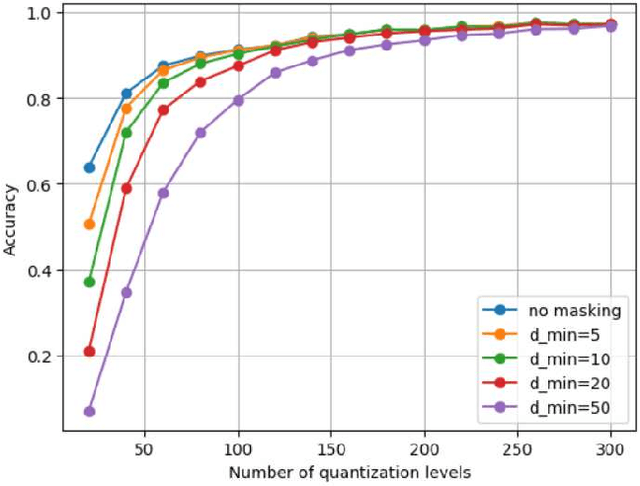
Abstract:Transparency and explainability are two extremely important aspects to be considered when employing black-box machine learning models in high-stake applications. Providing counterfactual explanations is one way of catering this requirement. However, this also poses a threat to the privacy of both the institution that is providing the explanation as well as the user who is requesting it. In this work, we propose multiple schemes inspired by private information retrieval (PIR) techniques which ensure the \emph{user's privacy} when retrieving counterfactual explanations. We present a scheme which retrieves the \emph{exact} nearest neighbor counterfactual explanation from a database of accepted points while achieving perfect (information-theoretic) privacy for the user. While the scheme achieves perfect privacy for the user, some leakage on the database is inevitable which we quantify using a mutual information based metric. Furthermore, we propose strategies to reduce this leakage to achieve an advanced degree of database privacy. We extend these schemes to incorporate user's preference on transforming their attributes, so that a more actionable explanation can be received. Since our schemes rely on finite field arithmetic, we empirically validate our schemes on real datasets to understand the trade-off between the accuracy and the finite field sizes.
Quantifying Prediction Consistency Under Model Multiplicity in Tabular LLMs
Jul 04, 2024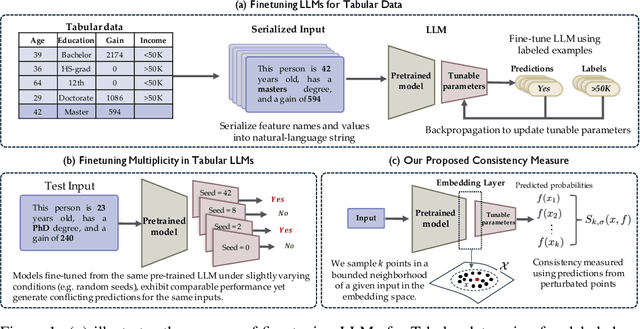
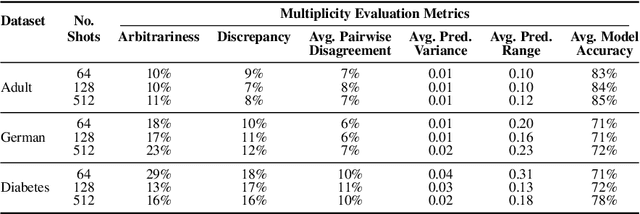
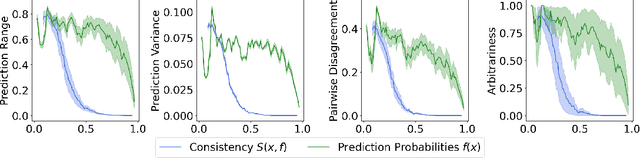
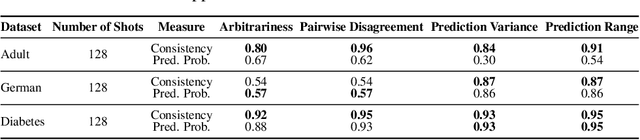
Abstract:Fine-tuning large language models (LLMs) on limited tabular data for classification tasks can lead to \textit{fine-tuning multiplicity}, where equally well-performing models make conflicting predictions on the same inputs due to variations in the training process (i.e., seed, random weight initialization, retraining on additional or deleted samples). This raises critical concerns about the robustness and reliability of Tabular LLMs, particularly when deployed for high-stakes decision-making, such as finance, hiring, education, healthcare, etc. This work formalizes the challenge of fine-tuning multiplicity in Tabular LLMs and proposes a novel metric to quantify the robustness of individual predictions without expensive model retraining. Our metric quantifies a prediction's stability by analyzing (sampling) the model's local behavior around the input in the embedding space. Interestingly, we show that sampling in the local neighborhood can be leveraged to provide probabilistic robustness guarantees against a broad class of fine-tuned models. By leveraging Bernstein's Inequality, we show that predictions with sufficiently high robustness (as defined by our measure) will remain consistent with high probability. We also provide empirical evaluation on real-world datasets to support our theoretical results. Our work highlights the importance of addressing fine-tuning instabilities to enable trustworthy deployment of LLMs in high-stakes and safety-critical applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge