Private Information Retrieval With Arbitrary Privacy Requirements for Graph-Based Storage

We reformulate the definition of privacy in the private information retrieval (PIR) problem to accommodate flexible privacy requirements. We focus on graph-replicated PIR, with a generalized privacy requirement, instead of requiring all messages to be private from all servers, during retrieval. Towards this, we define a privacy requirement set for each server, which can be an arbitrary subset of all message indices, as long as the stored message indices are in their privacy requirement set. Since both the storage and privacy requirement sets have many possibilities, we focus on two specific storage settings, namely the path and cyclic graphs. We consider several privacy settings for each of them, which are not necessarily the same, to give different examples for privacy sets. Of particular interest are the privacy sets that comprise the indices of messages stored at servers within a neighborhood range. The neighborhood range parameter allows a transition from the recently introduced local PIR [1] to the standard graph-replicated PIR. In these cases, we derive bounds on the capacity or find the exact capacity.

Local Private Information Retrieval: A New Privacy Perspective for Graph-Based Replicated Systems

We rethink the definition of privacy in multi-server, graph-replicated private information retrieval (PIR) systems, and introduce a novel setting where the user's privacy is governed by the servers' storage structure. In particular, while retrieving a message from a server, the user is concerned with hiding their desired message index from the server, only if the server stores the corresponding message. We coin this privacy requirement as local user privacy and the resulting PIR problem as local PIR on the graph. Our goal is to measure the gain in communication efficiency of local PIR, compared to that of canonical PIR, by establishing its capacity, i.e., the maximum number of message symbols retrieved, per downloaded symbol. To this end, we observe a remarkable gain in the local PIR capacity of graphs, that are disjoint union of distinct graphs, which is multiplicative, compared to the PIR capacity, when the individual graphs are identical. For connected graphs, we propose schemes to establish capacity lower bounds for edge-transitive and bipartite graphs, which are greater than the best-known PIR capacity bounds. Finally, we derive the exact local PIR capacity for the cyclic graph, and the path graph with an odd number of vertices.

The Role of Common Randomness Replication in Symmetric PIR on Graph-Based Replicated Systems

In symmetric private information retrieval (SPIR), a user communicates with multiple servers to retrieve from them a message in a database, while not revealing the message index to any individual server (user privacy), and learning no additional information about the database (database privacy). We study the problem of SPIR on graph-replicated database systems, where each node of the graph represents a server and each link represents a message. Each message is replicated at exactly two servers; those at which the link representing the message is incident. To ensure database privacy, the servers share a set of common randomness, independent of the database and the user's desired message index. We study two cases of common randomness distribution to the servers: i) graph-replicated common randomness, and ii) fully-replicated common randomness. Given a graph-replicated database system, in i), we assign one randomness variable independently to every pair of servers sharing a message, while in ii), we assign an identical set of randomness variable to all servers, irrespective of the underlying graph. In both settings, our goal is to characterize the SPIR capacity, i.e., the maximum number of desired message symbols retrieved per downloaded symbol, and quantify the minimum amount of common randomness required to achieve the capacity. To this goal, in setting i), we derive a general lower bound on the SPIR capacity, and show it to be tight for path and regular graphs through a matching converse. Moreover, we establish that the minimum size of common randomness required for SPIR is equal to the message size. In setting ii), the SPIR capacity improves over the first, more restrictive setting. We show this through capacity lower bounds for a class of graphs, by constructing SPIR schemes from PIR schemes.

HetDAPAC: Leveraging Attribute Heterogeneity in Distributed Attribute-Based Private Access Control

Verifying user attributes to provide fine-grained access control to databases is fundamental to attribute-based authentication. Either a single (central) authority verifies all the attributes, or multiple independent authorities verify the attributes distributedly. In the central setup, the authority verifies all user attributes, and the user downloads only the authorized record. While this is communication efficient, it reveals all user attributes to the authority. A distributed setup prevents this privacy breach by letting each authority verify and learn only one attribute. Motivated by this, Jafarpisheh~et~al. introduced an information-theoretic formulation, called distributed attribute-based private access control (DAPAC). With $N$ non-colluding authorities (servers), $N$ attributes and $K$ possible values for each attribute, the DAPAC system lets each server learn only the single attribute value that it verifies, and is oblivious to the remaining $N-1$. The user retrieves its designated record, without learning anything about the remaining database records. The goal is to maximize the rate, i.e., the ratio of desired message size to total download size. However, not all attributes are sensitive, and DAPAC's privacy constraints can be too restrictive, negatively affecting the rate. To leverage the heterogeneous privacy requirements of user attributes, we propose heterogeneous (Het)DAPAC, a framework which off-loads verification of $N-D$ of the $N$ attributes to a central server, and retains DAPAC's architecture for the $D$ sensitive attributes. We first present a HetDAPAC scheme, which improves the rate from $\frac{1}{2K}$ to $\frac{1}{K+1}$, while sacrificing the privacy of a few non-sensitive attributes. Unlike DAPAC, our scheme entails a download imbalance across servers; we propose a second scheme achieving a balanced per-server download and a rate of $\frac{D+1}{2KD}$.

Effect of Full Common Randomness Replication in Symmetric PIR on Graph-Based Replicated Systems

We revisit the problem of symmetric private information retrieval (SPIR) in settings where the database replication is modeled by a simple graph. Here, each vertex corresponds to a server, and a message is replicated on two servers if and only if there is an edge between them. To satisfy the requirement of database privacy, we let all the servers share some common randomness, independent of the messages. We aim to quantify the improvement in SPIR capacity, i.e., the maximum ratio of the number of desired and downloaded symbols, compared to the setting with graph-replicated common randomness. Towards this, we develop an algorithm to convert a class of PIR schemes into the corresponding SPIR schemes, thereby establishing a capacity lower bound on graphs for which such schemes exist. This includes the class of path and cyclic graphs for which we derive capacity upper bounds that are tighter than the trivial bounds given by the respective PIR capacities. For the special case of path graph with three vertices, we identify the SPIR capacity to be $\frac{1}{2}$.

Multi-Agent Distributed Optimization With Feasible Set Privacy

We consider the problem of decentralized constrained optimization with multiple agents $E_1,\ldots,E_N$ who jointly wish to learn the optimal solution set while keeping their feasible sets $\mathcal{P}_1,\ldots,\mathcal{P}_N$ private from each other. We assume that the objective function $f$ is known to all agents and each feasible set is a collection of points from a universal alphabet $\mathcal{P}_{alph}$. A designated agent (leader) starts the communication with the remaining (non-leader) agents, and is the first to retrieve the solution set. The leader searches for the solution by sending queries to and receiving answers from the non-leaders, such that the information on the individual feasible sets revealed to the leader should be no more than nominal, i.e., what is revealed from learning the solution set alone. We develop achievable schemes for obtaining the solution set at nominal information leakage, and characterize their communication costs under two communication setups between agents. In this work, we focus on two kinds of network setups: i) ring, where each agent communicates with two adjacent agents, and ii) star, where only the leader communicates with the remaining agents. We show that, if the leader first learns the joint feasible set through an existing private set intersection (PSI) protocol and then deduces the solution set, the information leaked to the leader is greater than nominal. Moreover, we draw connection of our schemes to threshold PSI (ThPSI), which is a PSI-variant where the intersection is revealed only when its cardinality is larger than a threshold value. Finally, for various realizations of $f$ mapped uniformly at random to a fixed range of values, our schemes are more communication-efficient with a high probability compared to retrieving the entire feasible set through PSI.

Symmetric Private Information Retrieval (SPIR) on Graph-Based Replicated Systems

We introduce the problem of symmetric private information retrieval (SPIR) on replicated databases modeled by a simple graph. In this model, each vertex corresponds to a server, and a message is replicated on two servers if and only if there is an edge between them. We consider the setting where the server-side common randomness necessary to accomplish SPIR is also replicated at the servers according to the graph, and we call this as message-specific common randomness. In this setting, we establish a lower bound on the SPIR capacity, i.e., the maximum download rate, for general graphs, by proposing an achievable SPIR scheme. Next, we prove that, for any SPIR scheme to be feasible, the minimum size of message-specific randomness should be equal to the size of a message. Finally, by providing matching upper bounds, we derive the exact SPIR capacity for the class of path and regular graphs.

Private Information Retrieval on Multigraph-Based Replicated Storage

We consider the private information retrieval (PIR) problem for a multigraph-based replication system, where each set of $r$ files is stored on two of the servers according to an underlying $r$-multigraph. Our goal is to establish upper and lower bounds on the PIR capacity of the $r$-multigraph. Specifically, we first propose a construction for multigraph-based PIR systems that leverages the symmetry of the underlying graph-based PIR scheme, deriving a capacity lower bound for such multigraphs. Then, we establish a general upper bound using linear programming, expressed as a function of the underlying graph parameters. Our bounds are demonstrated to be tight for PIR systems on multipaths for even number of vertices.

Private Counterfactual Retrieval With Immutable Features

In a classification task, counterfactual explanations provide the minimum change needed for an input to be classified into a favorable class. We consider the problem of privately retrieving the exact closest counterfactual from a database of accepted samples while enforcing that certain features of the input sample cannot be changed, i.e., they are \emph{immutable}. An applicant (user) whose feature vector is rejected by a machine learning model wants to retrieve the sample closest to them in the database without altering a private subset of their features, which constitutes the immutable set. While doing this, the user should keep their feature vector, immutable set and the resulting counterfactual index information-theoretically private from the institution. We refer to this as immutable private counterfactual retrieval (I-PCR) problem which generalizes PCR to a more practical setting. In this paper, we propose two I-PCR schemes by leveraging techniques from private information retrieval (PIR) and characterize their communication costs. Further, we quantify the information that the user learns about the database and compare it for the proposed schemes.

Private Counterfactual Retrieval

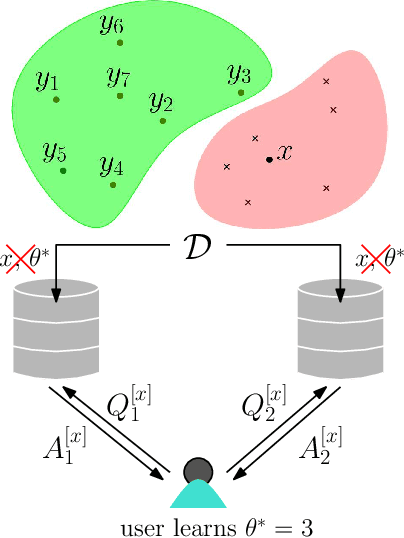
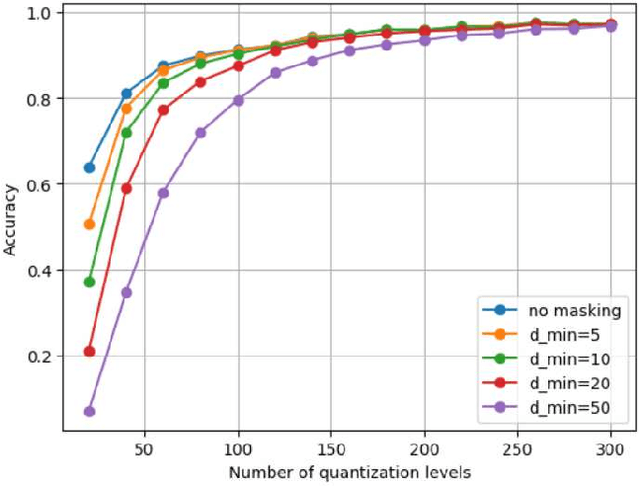
Transparency and explainability are two extremely important aspects to be considered when employing black-box machine learning models in high-stake applications. Providing counterfactual explanations is one way of catering this requirement. However, this also poses a threat to the privacy of both the institution that is providing the explanation as well as the user who is requesting it. In this work, we propose multiple schemes inspired by private information retrieval (PIR) techniques which ensure the \emph{user's privacy} when retrieving counterfactual explanations. We present a scheme which retrieves the \emph{exact} nearest neighbor counterfactual explanation from a database of accepted points while achieving perfect (information-theoretic) privacy for the user. While the scheme achieves perfect privacy for the user, some leakage on the database is inevitable which we quantify using a mutual information based metric. Furthermore, we propose strategies to reduce this leakage to achieve an advanced degree of database privacy. We extend these schemes to incorporate user's preference on transforming their attributes, so that a more actionable explanation can be received. Since our schemes rely on finite field arithmetic, we empirically validate our schemes on real datasets to understand the trade-off between the accuracy and the finite field sizes.