The Asymptotic Capacity of Byzantine Symmetric Private Information Retrieval and Its Consequences

We consider the problem of finding the asymptotic capacity of symmetric private information retrieval (SPIR) with $B$ Byzantine servers. Prior to finding the capacity, a definition for the Byzantine servers is needed since in the literature there are two different definitions. In \cite{byzantine_tpir}, where it was first defined, the Byzantine servers can send any symbol from the storage, their received queries and some independent random symbols. In \cite{unresponsive_byzantine_1}, Byzantine servers send any random symbol independently of their storage and queries. It is clear that these definitions are not identical, especially when \emph{symmetric} privacy is required. To that end, we define Byzantine servers, inspired by \cite{byzantine_tpir}, as the servers that can share everything, before and after the scheme initiation. In this setting, we find an upper bound, for an infinite number of messages case, that should be satisfied for all schemes that protect against this setting and develop a scheme that achieves this upper bound. Hence, we identify the capacity of the problem.

Entanglement-Assisted Coding for Arbitrary Linear Computations Over a Quantum MAC

We study a linear computation problem over a quantum multiple access channel (LC-QMAC), where $S$ servers share an entangled state and separately store classical data streams $W_1,\cdots, W_S$ over a finite field $\mathbb{F}_d$. A user aims to compute $K$ linear combinations of these data streams, represented as $Y = \mathbf{V}_1 W_1 + \mathbf{V}_2 W_2 + \cdots + \mathbf{V}_S W_S \in \mathbb{F}_d^{K \times 1}$. To this end, each server encodes its classical information into its local quantum subsystem and transmits it to the user, who retrieves the desired computations via quantum measurements. In this work, we propose an achievable scheme for LC-QMAC based on the stabilizer formalism and the ideas from entanglement-assisted quantum error-correcting codes (EAQECC). Specifically, given any linear computation matrix, we construct a self-orthogonal matrix that can be implemented using the stabilizer formalism. Also, we apply precoding matrices to minimize the number of auxiliary qudits required. Our scheme achieves more computations per qudit, i.e., a higher computation rate, compared to the best-known methods in the literature, and attains the capacity in certain cases.

Byzantine-Eavesdropper Alliance: How to Achieve Symmetric Privacy in Quantum $X$-Secure $B$-Byzantine $E$-Eavesdropped $U$-Unresponsive $T$-Colluding PIR?

We consider the quantum \emph{symmetric} private information retrieval (QSPIR) problem in a system with $N$ databases and $K$ messages, with $U$ unresponsive servers, $T$-colluding servers, and $X$-security parameter, under several fundamental threat models. In the first model, there are $\mathcal{E}_1$ eavesdropped links in the uplink direction (the direction from the user to the $N$ servers), $\mathcal{E}_2$ eavesdropped links in the downlink direction (the direction from the servers to the user), where $|\mathcal{E}_1|, |\mathcal{E}_2| \leq E$; we coin this eavesdropper setting as \emph{dynamic} eavesdroppers. We show that super-dense coding gain can be achieved for some regimes. In the second model, we consider the case with Byzantine servers, i.e., servers that can coordinate to devise a plan to harm the privacy and security of the system together with static eavesdroppers, by listening to the same links in both uplink and downlink directions. It is important to note the considerable difference between the two threat models, since the eavesdroppers can take huge advantage of the presence of the Byzantine servers. Unlike the previous works in SPIR with Byzantine servers, that assume that the Byzantine servers can send only random symbols independent of the stored messages, we follow the definition of Byzantine servers in \cite{byzantine_tpir}, where the Byzantine servers can send symbols that can be functions of the storage, queries, as well as the random symbols in a way that can produce worse harm to the system. In the third and the most novel threat model, we consider the presence of Byzantine servers and dynamic eavesdroppers together. We show that having dynamic eavesdroppers along with Byzantine servers in the same system model creates more threats to the system than having static eavesdroppers with Byzantine servers.

Private Counterfactual Retrieval With Immutable Features

In a classification task, counterfactual explanations provide the minimum change needed for an input to be classified into a favorable class. We consider the problem of privately retrieving the exact closest counterfactual from a database of accepted samples while enforcing that certain features of the input sample cannot be changed, i.e., they are \emph{immutable}. An applicant (user) whose feature vector is rejected by a machine learning model wants to retrieve the sample closest to them in the database without altering a private subset of their features, which constitutes the immutable set. While doing this, the user should keep their feature vector, immutable set and the resulting counterfactual index information-theoretically private from the institution. We refer to this as immutable private counterfactual retrieval (I-PCR) problem which generalizes PCR to a more practical setting. In this paper, we propose two I-PCR schemes by leveraging techniques from private information retrieval (PIR) and characterize their communication costs. Further, we quantify the information that the user learns about the database and compare it for the proposed schemes.

Private Counterfactual Retrieval

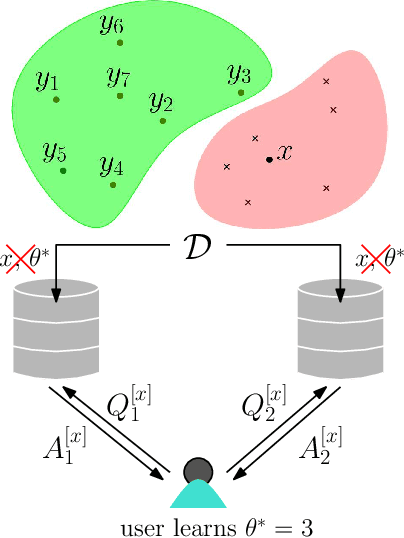
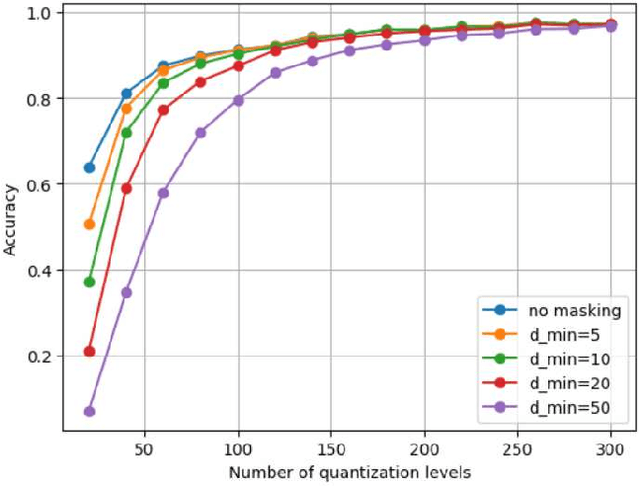
Transparency and explainability are two extremely important aspects to be considered when employing black-box machine learning models in high-stake applications. Providing counterfactual explanations is one way of catering this requirement. However, this also poses a threat to the privacy of both the institution that is providing the explanation as well as the user who is requesting it. In this work, we propose multiple schemes inspired by private information retrieval (PIR) techniques which ensure the \emph{user's privacy} when retrieving counterfactual explanations. We present a scheme which retrieves the \emph{exact} nearest neighbor counterfactual explanation from a database of accepted points while achieving perfect (information-theoretic) privacy for the user. While the scheme achieves perfect privacy for the user, some leakage on the database is inevitable which we quantify using a mutual information based metric. Furthermore, we propose strategies to reduce this leakage to achieve an advanced degree of database privacy. We extend these schemes to incorporate user's preference on transforming their attributes, so that a more actionable explanation can be received. Since our schemes rely on finite field arithmetic, we empirically validate our schemes on real datasets to understand the trade-off between the accuracy and the finite field sizes.

Quantum $X$-Secure $B$-Byzantine $T$-Colluding Private Information Retrieval

We consider the problems arising from the presence of Byzantine servers in a quantum private information retrieval (QPIR) setting. This is the first work to precisely define what the capabilities of Byzantine servers could be in a QPIR context. We show that quantum Byzantine servers have more capabilities than their classical counterparts due to the possibilities created by the quantum encoding procedure. We focus on quantum Byzantine servers that can apply any reversible operations on their individual qudits. In this case, the Byzantine servers can generate any error, i.e., this covers \emph{all} possible single qudit operations that can be done by the Byzantine servers on their qudits. We design a scheme that is resilient to these kinds of manipulations. We show that the scheme designed achieves superdense coding gain in all cases, i.e., $R_Q= \max \left\{0,\min\left\{1,2\left(1-\frac{X+T+2B}{N}\right)\right\}\right\}$.

Quantum Private Membership Aggregation

We consider the problem of private set membership aggregation of $N$ parties by using an entangled quantum state. In this setting, the $N$ parties, which share an entangled state, aim to \emph{privately} know the number of times each element (message) is repeated among the $N$ parties, with respect to a universal set $\mathcal{K}$. This problem has applications in private comparison, ranking, voting, etc. We propose an encoding algorithm that maps the classical information into distinguishable quantum states, along with a decoding algorithm that exploits the distinguishability of the mapped states. The proposed scheme can also be used to calculate the $N$ party private summation modulo $P$.

Private Membership Aggregation

We consider the problem of private membership aggregation (PMA), in which a user counts the number of times a certain element is stored in a system of independent parties that store arbitrary sets of elements from a universal alphabet. The parties are not allowed to learn which element is being counted by the user. Further, neither the user nor the other parties are allowed to learn the stored elements of each party involved in the process. PMA is a generalization of the recently introduced problem of $K$ private set intersection ($K$-PSI). The $K$-PSI problem considers a set of $M$ parties storing arbitrary sets of elements, and a user who wants to determine if a certain element is repeated at least at $K$ parties out of the $M$ parties without learning which party has the required element and which party does not. To solve the general problem of PMA, we dissect it into four categories based on the privacy requirement and the collusions among databases/parties. We map these problems into equivalent private information retrieval (PIR) problems. We propose achievable schemes for each of the four variants of the problem based on the concept of cross-subspace alignment (CSA). The proposed schemes achieve \emph{linear} communication complexity as opposed to the state-of-the-art $K$-PSI scheme that requires \emph{exponential} complexity even though our PMA problems contain more security and privacy constraints.

Quantum Symmetric Private Information Retrieval with Secure Storage and Eavesdroppers

We consider both the classical and quantum variations of $X$-secure, $E$-eavesdropped and $T$-colluding symmetric private information retrieval (SPIR). This is the first work to study SPIR with $X$-security in classical or quantum variations. We first develop a scheme for classical $X$-secure, $E$-eavesdropped and $T$-colluding SPIR (XSETSPIR) based on a modified version of cross subspace alignment (CSA), which achieves a rate of $R= 1 - \frac{X+\max(T,E)}{N}$. The modified scheme achieves the same rate as the scheme used for $X$-secure PIR with the extra benefit of symmetric privacy. Next, we extend this scheme to its quantum counterpart based on the $N$-sum box abstraction. This is the first work to consider the presence of eavesdroppers in quantum private information retrieval (QPIR). In the quantum variation, the eavesdroppers have better access to information over the quantum channel compared to the classical channel due to the over-the-air decodability. To that end, we develop another scheme specialized to combat eavesdroppers over quantum channels. The scheme proposed for $X$-secure, $E$-eavesdropped and $T$-colluding quantum SPIR (XSETQSPIR) in this work maintains the super-dense coding gain from the shared entanglement between the databases, i.e., achieves a rate of $R_Q = \min\left\{ 1, 2\left(1-\frac{X+\max(T,E)}{N}\right)\right\}$.

Asymmetric $X$-Secure $T$-Private Information Retrieval: More Databases is Not Always Better

We consider a special case of $X$-secure $T$-private information retrieval (XSTPIR), where the security requirement is \emph{asymmetric} due to possible missing communication links between the $N$ databases considered in the system. We define the problem with a communication matrix that indicates all possible communications among the databases, and propose a database grouping mechanism that collects subsets of databases in an optimal manner, followed by a group-based PIR scheme to perform asymmetric XSTPIR with the goal of maximizing the communication rate (minimizing the download cost). We provide an upper bound on the general achievable rate of asymmetric XSTPIR, and show that the proposed scheme achieves this upper bound in some cases. The proposed approach outperforms classical XSTPIR under certain conditions, and the results of this work show that unlike in the symmetric case, some databases with certain properties can be dropped to achieve higher rates, concluding that more databases is not always better.