Private Information Retrieval on Multigraph-Based Replicated Storage

We consider the private information retrieval (PIR) problem for a multigraph-based replication system, where each set of $r$ files is stored on two of the servers according to an underlying $r$-multigraph. Our goal is to establish upper and lower bounds on the PIR capacity of the $r$-multigraph. Specifically, we first propose a construction for multigraph-based PIR systems that leverages the symmetry of the underlying graph-based PIR scheme, deriving a capacity lower bound for such multigraphs. Then, we establish a general upper bound using linear programming, expressed as a function of the underlying graph parameters. Our bounds are demonstrated to be tight for PIR systems on multipaths for even number of vertices.

Gradient Coding from Cyclic MDS Codes and Expander Graphs

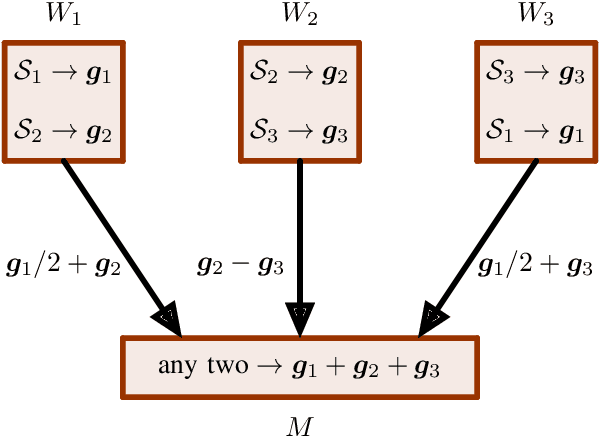
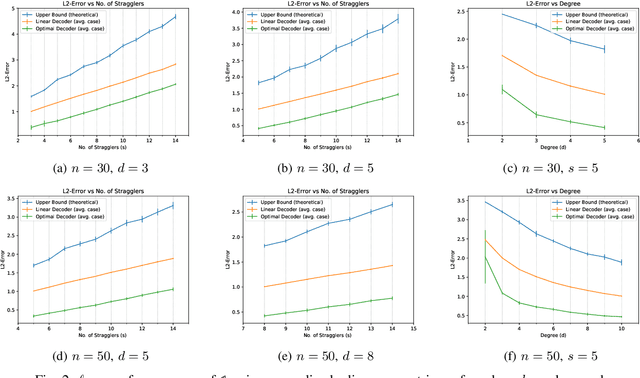
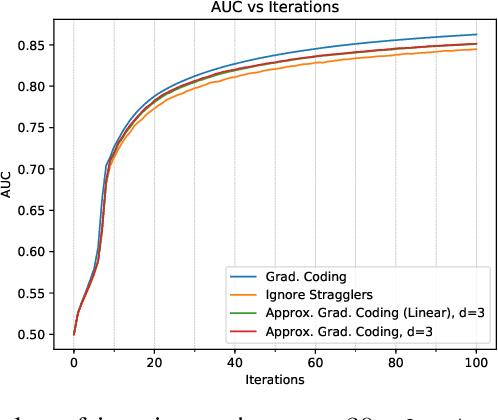
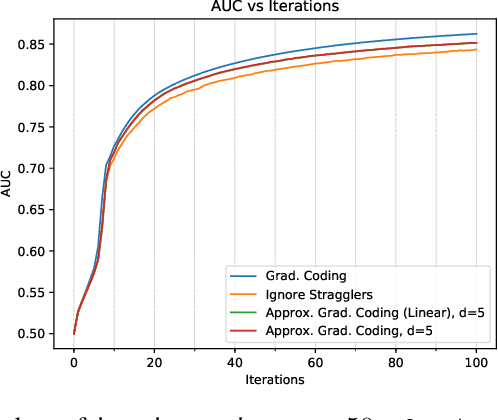
Gradient coding is a technique for straggler mitigation in distributed learning. In this paper we design novel gradient codes using tools from classical coding theory, namely, cyclic MDS codes, which compare favourably with existing solutions, both in the applicable range of parameters and in the complexity of the involved algorithms. Second, we introduce an approximate variant of the gradient coding problem, in which we settle for approximate gradient computation instead of the exact one. This approach enables graceful degradation, i.e., the $\ell_2$ error of the approximate gradient is a decreasing function of the number of stragglers. Our main result is that the normalized adjacency matrix of an expander graph can yield excellent approximate gradient codes, and that this approach allows us to perform significantly less computation compared to exact gradient coding. We experimentally test our approach on Amazon EC2, and show that the generalization error of approximate gradient coding is very close to the full gradient while requiring significantly less computation from the workers.