Robust Counterfactual Explanations for Neural Networks With Probabilistic Guarantees
Paper and Code
May 19, 2023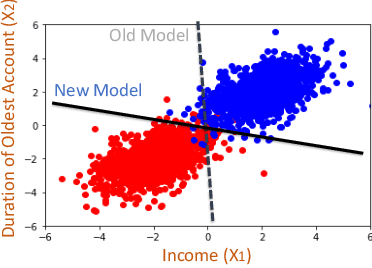
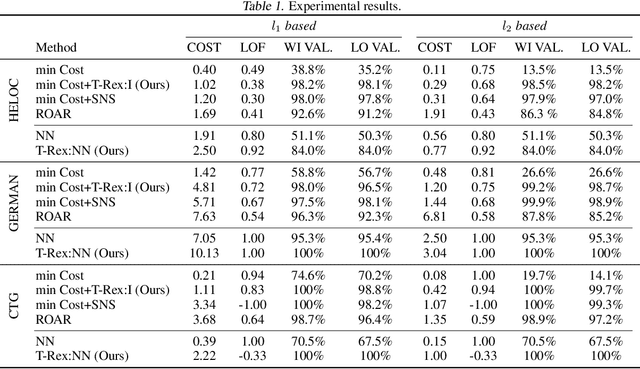
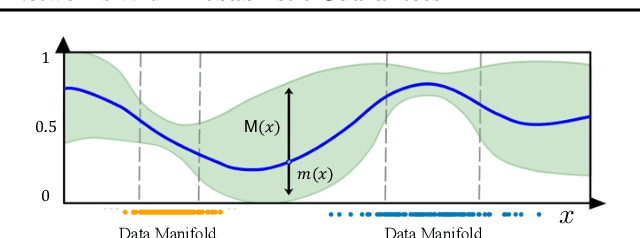
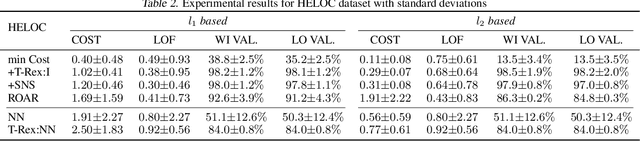
There is an emerging interest in generating robust counterfactual explanations that would remain valid if the model is updated or changed even slightly. Towards finding robust counterfactuals, existing literature often assumes that the original model $m$ and the new model $M$ are bounded in the parameter space, i.e., $\|\text{Params}(M){-}\text{Params}(m)\|{<}\Delta$. However, models can often change significantly in the parameter space with little to no change in their predictions or accuracy on the given dataset. In this work, we introduce a mathematical abstraction termed \emph{naturally-occurring} model change, which allows for arbitrary changes in the parameter space such that the change in predictions on points that lie on the data manifold is limited. Next, we propose a measure -- that we call \emph{Stability} -- to quantify the robustness of counterfactuals to potential model changes for differentiable models, e.g., neural networks. Our main contribution is to show that counterfactuals with sufficiently high value of \emph{Stability} as defined by our measure will remain valid after potential ``naturally-occurring'' model changes with high probability (leveraging concentration bounds for Lipschitz function of independent Gaussians). Since our quantification depends on the local Lipschitz constant around a data point which is not always available, we also examine practical relaxations of our proposed measure and demonstrate experimentally how they can be incorporated to find robust counterfactuals for neural networks that are close, realistic, and remain valid after potential model changes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge