Distributed Risk-Sensitive Safety Filters for Uncertain Discrete-Time Systems

Ensuring safety in multi-agent systems is a significant challenge, particularly in settings where centralized coordination is impractical. In this work, we propose a novel risk-sensitive safety filter for discrete-time multi-agent systems with uncertain dynamics that leverages control barrier functions (CBFs) defined through value functions. Our approach relies on centralized risk-sensitive safety conditions based on exponential risk operators to ensure robustness against model uncertainties. We introduce a distributed formulation of the safety filter by deriving two alternative strategies: one based on worst-case anticipation and another on proximity to a known safe policy. By allowing agents to switch between strategies, feasibility can be ensured. Through detailed numerical evaluations, we demonstrate the efficacy of our approach in maintaining safety without being overly conservative.

Koopman-Equivariant Gaussian Processes

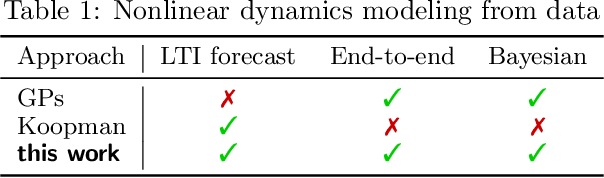
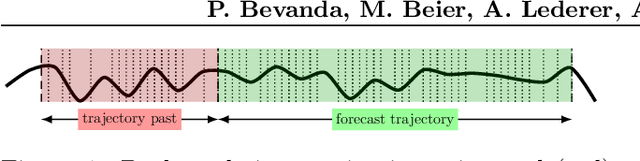
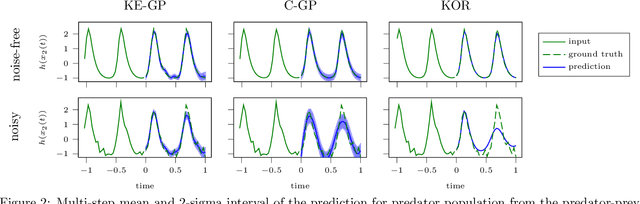
Credible forecasting and representation learning of dynamical systems are of ever-increasing importance for reliable decision-making. To that end, we propose a family of Gaussian processes (GP) for dynamical systems with linear time-invariant responses, which are nonlinear only in initial conditions. This linearity allows us to tractably quantify forecasting and representational uncertainty, simultaneously alleviating the challenge of computing the distribution of trajectories from a GP-based dynamical system and enabling a new probabilistic treatment of learning Koopman operator representations. Using a trajectory-based equivariance -- which we refer to as \textit{Koopman equivariance} -- we obtain a GP model with enhanced generalization capabilities. To allow for large-scale regression, we equip our framework with variational inference based on suitable inducing points. Experiments demonstrate on-par and often better forecasting performance compared to kernel-based methods for learning dynamical systems.

Stable Inverse Reinforcement Learning: Policies from Control Lyapunov Landscapes

Learning from expert demonstrations to flexibly program an autonomous system with complex behaviors or to predict an agent's behavior is a powerful tool, especially in collaborative control settings. A common method to solve this problem is inverse reinforcement learning (IRL), where the observed agent, e.g., a human demonstrator, is assumed to behave according to the optimization of an intrinsic cost function that reflects its intent and informs its control actions. While the framework is expressive, it is also computationally demanding and generally lacks convergence guarantees. We therefore propose a novel, stability-certified IRL approach by reformulating the cost function inference problem to learning control Lyapunov functions (CLF) from demonstrations data. By additionally exploiting closed-form expressions for associated control policies, we are able to efficiently search the space of CLFs by observing the attractor landscape of the induced dynamics. For the construction of the inverse optimal CLFs, we use a Sum of Squares and formulate a convex optimization problem. We present a theoretical analysis of the optimality properties provided by the CLF and evaluate our approach using both simulated and real-world data.

Data-driven Force Observer for Human-Robot Interaction with Series Elastic Actuators using Gaussian Processes

Ensuring safety and adapting to the user's behavior are of paramount importance in physical human-robot interaction. Thus, incorporating elastic actuators in the robot's mechanical design has become popular, since it offers intrinsic compliance and additionally provide a coarse estimate for the interaction force by measuring the deformation of the elastic components. While observer-based methods have been shown to improve these estimates, they rely on accurate models of the system, which are challenging to obtain in complex operating environments. In this work, we overcome this issue by learning the unknown dynamics components using Gaussian process (GP) regression. By employing the learned model in a Bayesian filtering framework, we improve the estimation accuracy and additionally obtain an observer that explicitly considers local model uncertainty in the confidence measure of the state estimate. Furthermore, we derive guaranteed estimation error bounds, thus, facilitating the use in safety-critical applications. We demonstrate the effectiveness of the proposed approach experimentally in a human-exoskeleton interaction scenario.

Cooperative Learning with Gaussian Processes for Euler-Lagrange Systems Tracking Control under Switching Topologies

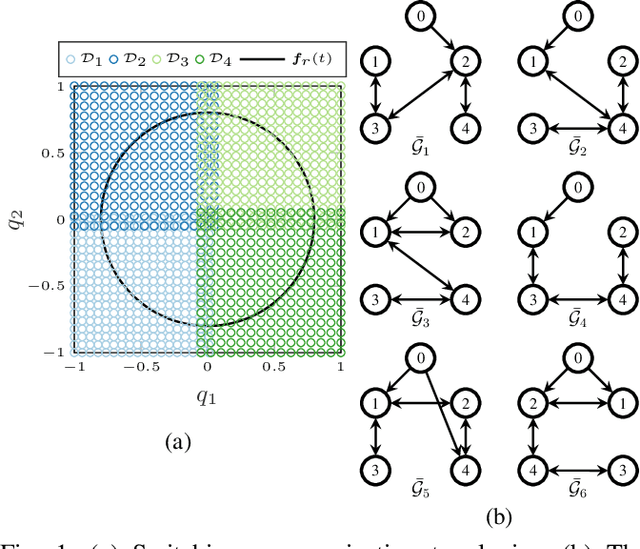
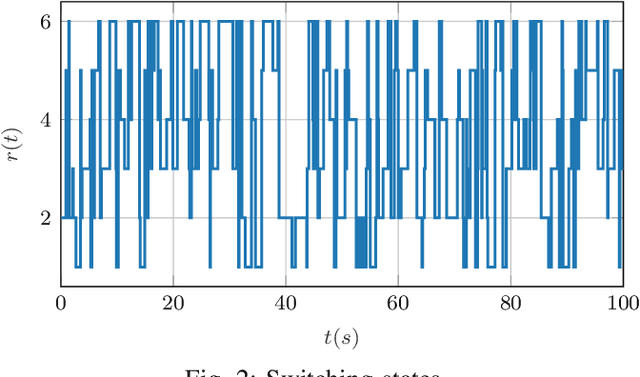
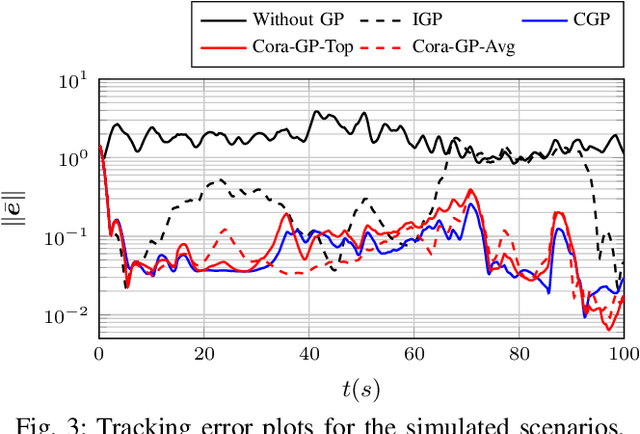
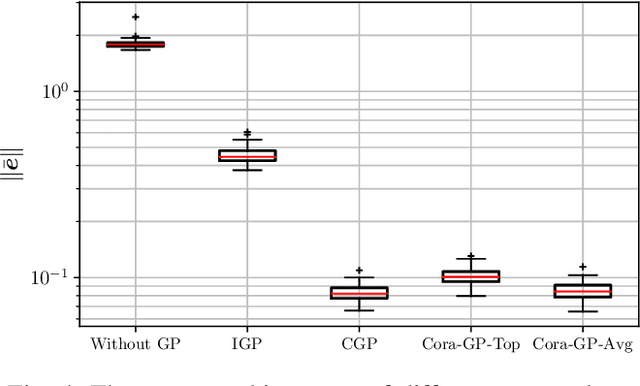
This work presents an innovative learning-based approach to tackle the tracking control problem of Euler-Lagrange multi-agent systems with partially unknown dynamics operating under switching communication topologies. The approach leverages a correlation-aware cooperative algorithm framework built upon Gaussian process regression, which adeptly captures inter-agent correlations for uncertainty predictions. A standout feature is its exceptional efficiency in deriving the aggregation weights achieved by circumventing the computationally intensive posterior variance calculations. Through Lyapunov stability analysis, the distributed control law ensures bounded tracking errors with high probability. Simulation experiments validate the protocol's efficacy in effectively managing complex scenarios, establishing it as a promising solution for robust tracking control in multi-agent systems characterized by uncertain dynamics and dynamic communication structures.

Episodic Gaussian Process-Based Learning Control with Vanishing Tracking Errors

Due to the increasing complexity of technical systems, accurate first principle models can often not be obtained. Supervised machine learning can mitigate this issue by inferring models from measurement data. Gaussian process regression is particularly well suited for this purpose due to its high data-efficiency and its explicit uncertainty representation, which allows the derivation of prediction error bounds. These error bounds have been exploited to show tracking accuracy guarantees for a variety of control approaches, but their direct dependency on the training data is generally unclear. We address this issue by deriving a Bayesian prediction error bound for GP regression, which we show to decay with the growth of a novel, kernel-based measure of data density. Based on the prediction error bound, we prove time-varying tracking accuracy guarantees for learned GP models used as feedback compensation of unknown nonlinearities, and show to achieve vanishing tracking error with increasing data density. This enables us to develop an episodic approach for learning Gaussian process models, such that an arbitrary tracking accuracy can be guaranteed. The effectiveness of the derived theory is demonstrated in several simulations.

Koopman Kernel Regression

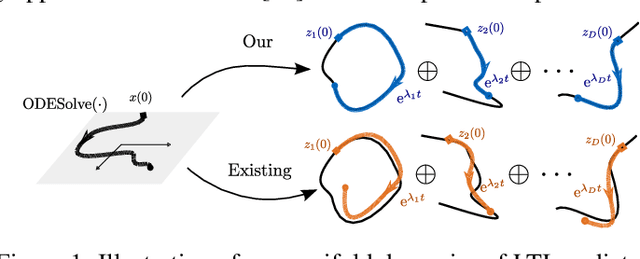
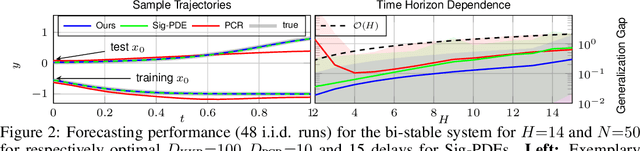
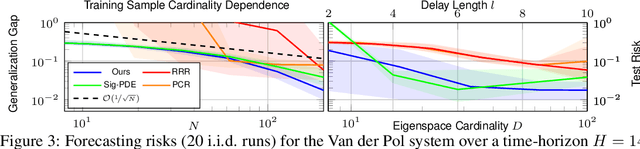
Many machine learning approaches for decision making, such as reinforcement learning, rely on simulators or predictive models to forecast the time-evolution of quantities of interest, e.g., the state of an agent or the reward of a policy. Forecasts of such complex phenomena are commonly described by highly nonlinear dynamical systems, making their use in optimization-based decision-making challenging. Koopman operator theory offers a beneficial paradigm for addressing this problem by characterizing forecasts via linear dynamical systems. This makes system analysis and long-term predictions simple -- involving only matrix multiplications. However, the transformation to a linear system is generally non-trivial and unknown, requiring learning-based approaches. While there exists a variety of approaches, they usually lack crucial learning-theoretic guarantees, such that the behavior of the obtained models with increasing data and dimensionality is often unclear. We address the aforementioned by deriving a novel reproducing kernel Hilbert space (RKHS) that solely spans transformations into linear dynamical systems. The resulting Koopman Kernel Regression (KKR) framework enables the use of statistical learning tools from function approximation for novel convergence results and generalization risk bounds under weaker assumptions than existing work. Our numerical experiments indicate advantages over state-of-the-art statistical learning approaches for Koopman-based predictors.

Can Learning Deteriorate Control? Analyzing Computational Delays in Gaussian Process-Based Event-Triggered Online Learning

When the dynamics of systems are unknown, supervised machine learning techniques are commonly employed to infer models from data. Gaussian process (GP) regression is a particularly popular learning method for this purpose due to the existence of prediction error bounds. Moreover, GP models can be efficiently updated online, such that event-triggered online learning strategies can be pursued to ensure specified tracking accuracies. However, existing trigger conditions must be able to be evaluated at arbitrary times, which cannot be achieved in practice due to non-negligible computation times. Therefore, we first derive a delay-aware tracking error bound, which reveals an accuracy-delay trade-off. Based on this result, we propose a novel event trigger for GP-based online learning with computational delays, which we show to offer advantages over offline trained GP models for sufficiently small computation times. Finally, we demonstrate the effectiveness of the proposed event trigger for online learning in simulations.

Learning-Based Optimal Control with Performance Guarantees for Unknown Systems with Latent States

As control engineering methods are applied to increasingly complex systems, data-driven approaches for system identification appear as a promising alternative to physics-based modeling. While many of these approaches rely on the availability of state measurements, the states of a complex system are often not directly measurable. It may then be necessary to jointly estimate the dynamics and a latent state, making it considerably more challenging to design controllers with performance guarantees. This paper proposes a novel method for the computation of an optimal input trajectory for unknown nonlinear systems with latent states. Probabilistic performance guarantees are derived for the resulting input trajectory, and an approach to validate the performance of arbitrary control laws is presented. The effectiveness of the proposed method is demonstrated in a numerical simulation.

Safe Learning-Based Control of Elastic Joint Robots via Control Barrier Functions

Ensuring safety is of paramount importance in physical human-robot interaction applications. This requires both an adherence to safety constraints defined on the system state, as well as guaranteeing compliant behaviour of the robot. If the underlying dynamical system is known exactly, the former can be addressed with the help of control barrier functions. Incorporation of elastic actuators in the robot's mechanical design can address the latter requirement. However, this elasticity can increase the complexity of the resulting system, leading to unmodeled dynamics, such that control barrier functions cannot directly ensure safety. In this paper, we mitigate this issue by learning the unknown dynamics using Gaussian process regression. By employing the model in a feedback linearizing control law, the safety conditions resulting from control barrier functions can be robustified to take into account model errors, while remaining feasible. In order enforce them on-line, we formulate the derived safety conditions in the form of a second-order cone program. We demonstrate our proposed approach with simulations on a two-degree of freedom planar robot with elastic joints.