Koopman-Equivariant Gaussian Processes

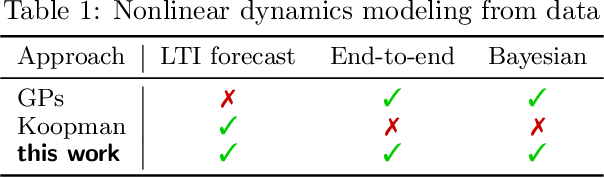
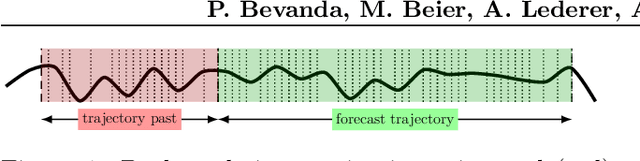
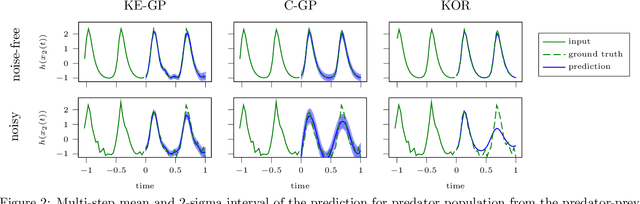
Credible forecasting and representation learning of dynamical systems are of ever-increasing importance for reliable decision-making. To that end, we propose a family of Gaussian processes (GP) for dynamical systems with linear time-invariant responses, which are nonlinear only in initial conditions. This linearity allows us to tractably quantify forecasting and representational uncertainty, simultaneously alleviating the challenge of computing the distribution of trajectories from a GP-based dynamical system and enabling a new probabilistic treatment of learning Koopman operator representations. Using a trajectory-based equivariance -- which we refer to as \textit{Koopman equivariance} -- we obtain a GP model with enhanced generalization capabilities. To allow for large-scale regression, we equip our framework with variational inference based on suitable inducing points. Experiments demonstrate on-par and often better forecasting performance compared to kernel-based methods for learning dynamical systems.

Koopman Kernel Regression

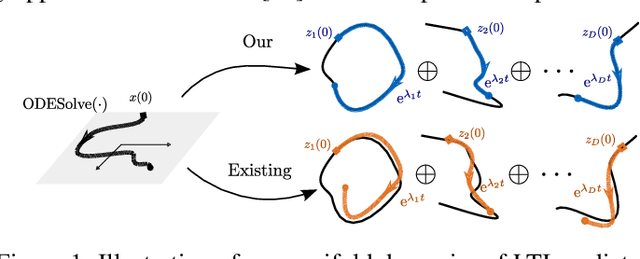
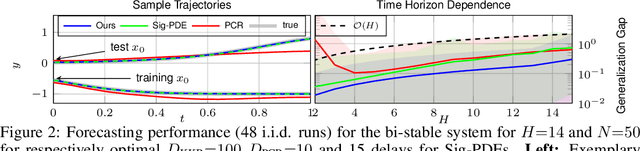
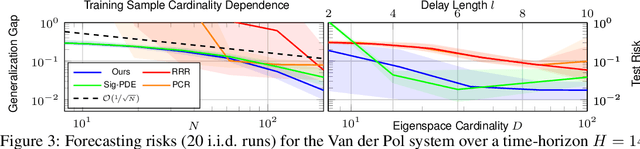
Many machine learning approaches for decision making, such as reinforcement learning, rely on simulators or predictive models to forecast the time-evolution of quantities of interest, e.g., the state of an agent or the reward of a policy. Forecasts of such complex phenomena are commonly described by highly nonlinear dynamical systems, making their use in optimization-based decision-making challenging. Koopman operator theory offers a beneficial paradigm for addressing this problem by characterizing forecasts via linear dynamical systems. This makes system analysis and long-term predictions simple -- involving only matrix multiplications. However, the transformation to a linear system is generally non-trivial and unknown, requiring learning-based approaches. While there exists a variety of approaches, they usually lack crucial learning-theoretic guarantees, such that the behavior of the obtained models with increasing data and dimensionality is often unclear. We address the aforementioned by deriving a novel reproducing kernel Hilbert space (RKHS) that solely spans transformations into linear dynamical systems. The resulting Koopman Kernel Regression (KKR) framework enables the use of statistical learning tools from function approximation for novel convergence results and generalization risk bounds under weaker assumptions than existing work. Our numerical experiments indicate advantages over state-of-the-art statistical learning approaches for Koopman-based predictors.

Towards Data-driven LQR with KoopmanizingFlows

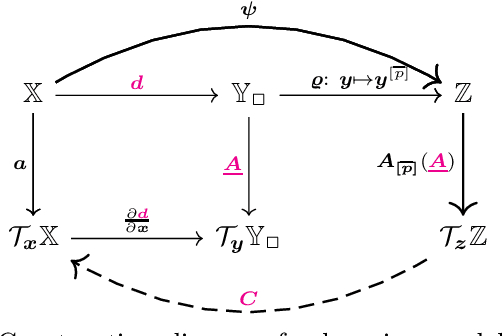
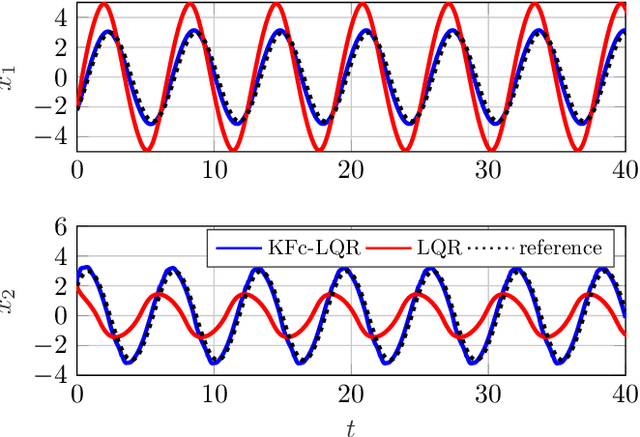
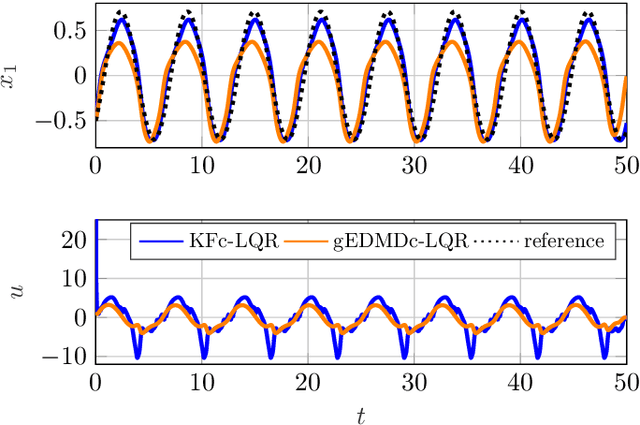
We propose a novel framework for learning linear time-invariant (LTI) models for a class of continuous-time non-autonomous nonlinear dynamics based on a representation of Koopman operators. In general, the operator is infinite-dimensional but, crucially, linear. To utilize it for efficient LTI control, we learn a finite representation of the Koopman operator that is linear in controls while concurrently learning meaningful lifting coordinates. For the latter, we rely on KoopmanizingFlows - a diffeomorphism-based representation of Koopman operators. With such a learned model, we can replace the nonlinear infinite-horizon optimal control problem with quadratic costs to that of a linear quadratic regulator (LQR), facilitating efficacious optimal control for nonlinear systems. The prediction and control efficacy of the proposed method is verified on simulation examples.

KoopmanizingFlows: Diffeomorphically Learning Stable Koopman Operators

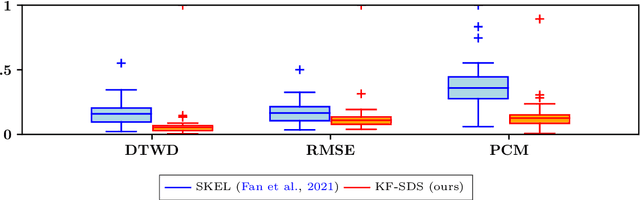
We propose a novel framework for constructing linear time-invariant (LTI) models for data-driven representations of the Koopman operator for a class of stable nonlinear dynamics. The Koopman operator (generator) lifts a finite-dimensional nonlinear system to a possibly infinite-dimensional linear feature space. To utilize it for modeling, one needs to discover finite-dimensional representations of the Koopman operator. Learning suitable features is challenging, as one needs to learn LTI features that are both Koopman-invariant (evolve linearly under the dynamics) as well as relevant (spanning the original state) - a generally unsupervised learning task. For a theoretically well-founded solution to this problem, we propose learning Koopman-invariant coordinates by composing a diffeomorphic learner with a lifted aggregate system of a latent linear model. Using an unconstrained parameterization of stable matrices along with the aforementioned feature construction, we learn the Koopman operator features without assuming a predefined library of functions or knowing the spectrum, while ensuring stability regardless of the operator approximation accuracy. We demonstrate the superior efficacy of the proposed method in comparison to a state-of-the-art method on the well-known LASA handwriting dataset.