Grasping in Uncertain Environments: A Case Study For Industrial Robotic Recycling

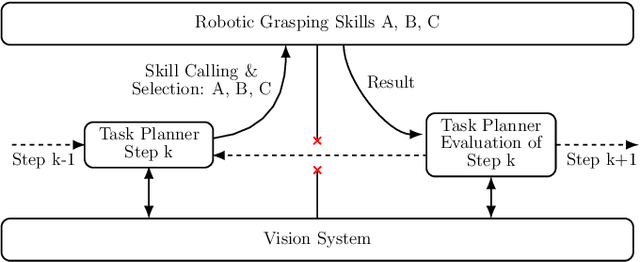
Autonomous robotic grasping of uncertain objects in uncertain environments is an impactful open challenge for the industries of the future. One such industry is the recycling of Waste Electrical and Electronic Equipment (WEEE) materials, in which electric devices are disassembled and readied for the recovery of raw materials. Since devices may contain hazardous materials and their disassembly involves heavy manual labor, robotic disassembly is a promising venue. However, since devices may be damaged, dirty and unidentified, robotic disassembly is challenging since object models are unavailable or cannot be relied upon. This case study explores grasping strategies for industrial robotic disassembly of WEEE devices with uncertain vision data. We propose three grippers and appropriate tactile strategies for force-based manipulation that improves grasping robustness. For each proposed gripper, we develop corresponding strategies that can perform effectively in different grasping tasks and leverage the grippers design and unique strengths. Through experiments conducted in lab and factory settings for four different WEEE devices, we demonstrate how object uncertainty may be overcome by tactile sensing and compliant techniques, significantly increasing grasping success rates.

KoopmanizingFlows: Diffeomorphically Learning Stable Koopman Operators

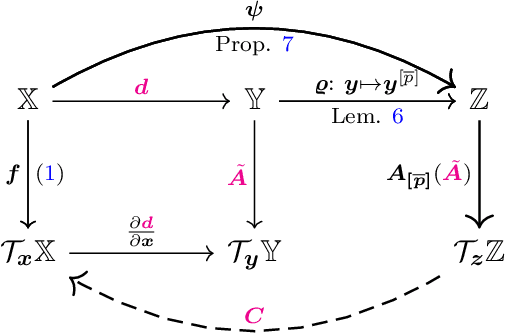
We propose a novel framework for constructing linear time-invariant (LTI) models for data-driven representations of the Koopman operator for a class of stable nonlinear dynamics. The Koopman operator (generator) lifts a finite-dimensional nonlinear system to a possibly infinite-dimensional linear feature space. To utilize it for modeling, one needs to discover finite-dimensional representations of the Koopman operator. Learning suitable features is challenging, as one needs to learn LTI features that are both Koopman-invariant (evolve linearly under the dynamics) as well as relevant (spanning the original state) - a generally unsupervised learning task. For a theoretically well-founded solution to this problem, we propose learning Koopman-invariant coordinates by composing a diffeomorphic learner with a lifted aggregate system of a latent linear model. Using an unconstrained parameterization of stable matrices along with the aforementioned feature construction, we learn the Koopman operator features without assuming a predefined library of functions or knowing the spectrum, while ensuring stability regardless of the operator approximation accuracy. We demonstrate the superior efficacy of the proposed method in comparison to a state-of-the-art method on the well-known LASA handwriting dataset.