Grasping in Uncertain Environments: A Case Study For Industrial Robotic Recycling

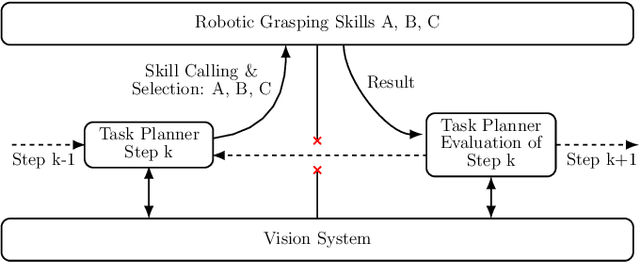
Autonomous robotic grasping of uncertain objects in uncertain environments is an impactful open challenge for the industries of the future. One such industry is the recycling of Waste Electrical and Electronic Equipment (WEEE) materials, in which electric devices are disassembled and readied for the recovery of raw materials. Since devices may contain hazardous materials and their disassembly involves heavy manual labor, robotic disassembly is a promising venue. However, since devices may be damaged, dirty and unidentified, robotic disassembly is challenging since object models are unavailable or cannot be relied upon. This case study explores grasping strategies for industrial robotic disassembly of WEEE devices with uncertain vision data. We propose three grippers and appropriate tactile strategies for force-based manipulation that improves grasping robustness. For each proposed gripper, we develop corresponding strategies that can perform effectively in different grasping tasks and leverage the grippers design and unique strengths. Through experiments conducted in lab and factory settings for four different WEEE devices, we demonstrate how object uncertainty may be overcome by tactile sensing and compliant techniques, significantly increasing grasping success rates.

MS2MP: A Min-Sum Message Passing Algorithm for Motion Planning

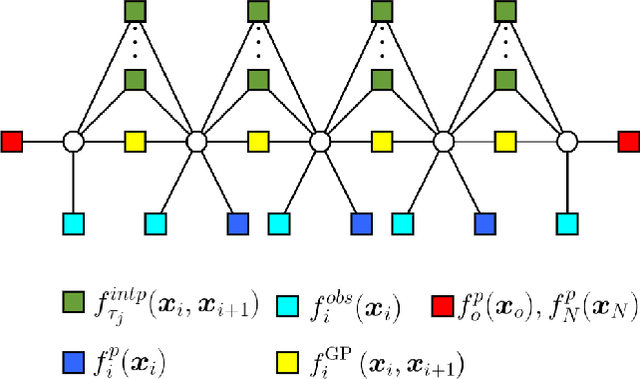
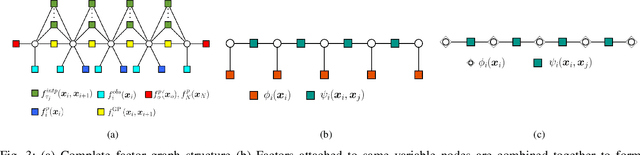
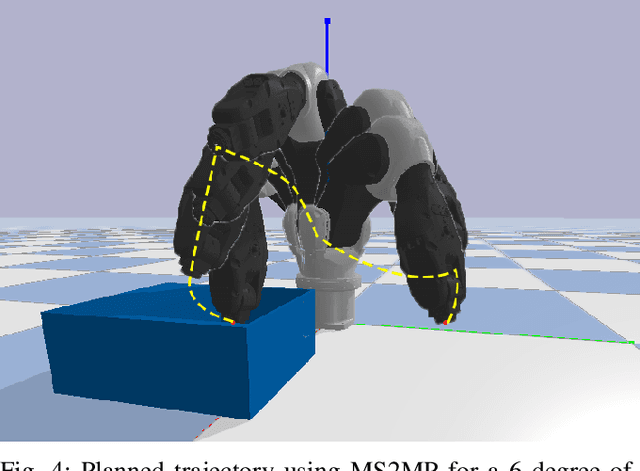
Gaussian Process (GP) formulation of continuoustime trajectory offers a fast solution to the motion planning problem via probabilistic inference on factor graph. However, often the solution converges to in-feasible local minima and the planned trajectory is not collision-free. We propose a message passing algorithm that is more sensitive to obstacles with fast convergence time. We leverage the utility of min-sum message passing algorithm that performs local computations at each node to solve the inference problem on factor graph. We first introduce the notion of compound factor node to transform the factor graph to a linearly structured graph. We next develop an algorithm denoted as Min-sum Message Passing algorithm for Motion Planning (MS2MP) that combines numerical optimization with message passing to find collision-free trajectories. MS2MP performs numerical optimization to solve non-linear least square minimization problem at each compound factor node and then exploits the linear structure of factor graph to compute the maximum a posteriori (MAP) estimation of complete graph by passing messages among graph nodes. The decentralized optimization approach of each compound node increases sensitivity towards avoiding obstacles for harder planning problems. We evaluate our algorithm by performing extensive experiments for exemplary motion planning tasks for a robot manipulator. Our evaluation reveals that MS2MP improves existing work in convergence time and success rate.

Reducing Overestimation Bias in Multi-Agent Domains Using Double Centralized Critics

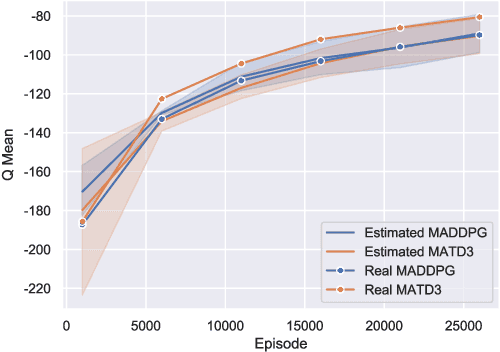
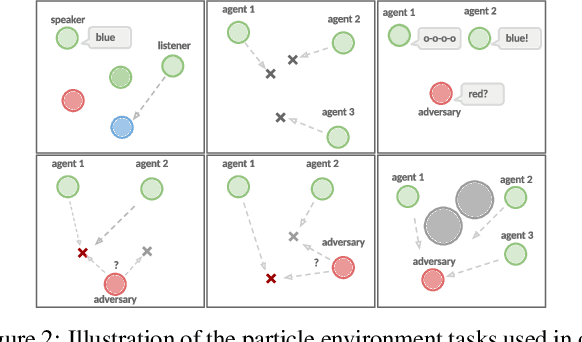
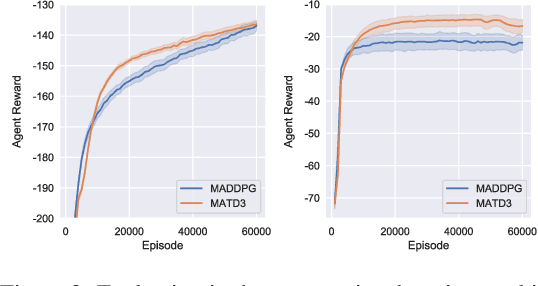
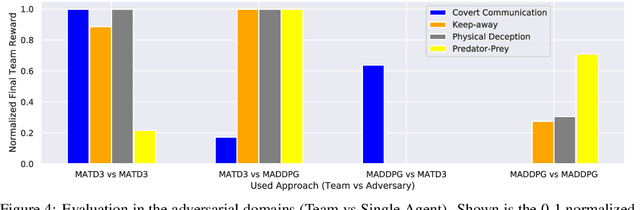
Many real world tasks require multiple agents to work together. Multi-agent reinforcement learning (RL) methods have been proposed in recent years to solve these tasks, but current methods often fail to efficiently learn policies. We thus investigate the presence of a common weakness in single-agent RL, namely value function overestimation bias, in the multi-agent setting. Based on our findings, we propose an approach that reduces this bias by using double centralized critics. We evaluate it on six mixed cooperative-competitive tasks, showing a significant advantage over current methods. Finally, we investigate the application of multi-agent methods to high-dimensional robotic tasks and show that our approach can be used to learn decentralized policies in this domain.