Grasping in Uncertain Environments: A Case Study For Industrial Robotic Recycling

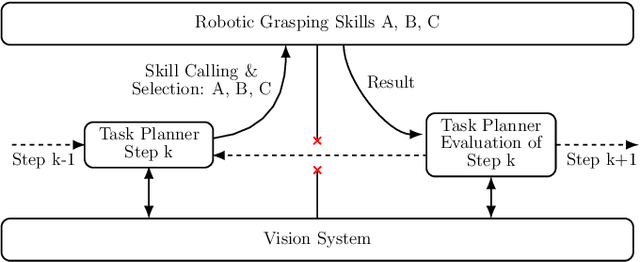
Autonomous robotic grasping of uncertain objects in uncertain environments is an impactful open challenge for the industries of the future. One such industry is the recycling of Waste Electrical and Electronic Equipment (WEEE) materials, in which electric devices are disassembled and readied for the recovery of raw materials. Since devices may contain hazardous materials and their disassembly involves heavy manual labor, robotic disassembly is a promising venue. However, since devices may be damaged, dirty and unidentified, robotic disassembly is challenging since object models are unavailable or cannot be relied upon. This case study explores grasping strategies for industrial robotic disassembly of WEEE devices with uncertain vision data. We propose three grippers and appropriate tactile strategies for force-based manipulation that improves grasping robustness. For each proposed gripper, we develop corresponding strategies that can perform effectively in different grasping tasks and leverage the grippers design and unique strengths. Through experiments conducted in lab and factory settings for four different WEEE devices, we demonstrate how object uncertainty may be overcome by tactile sensing and compliant techniques, significantly increasing grasping success rates.

A Fast Approach to Minimum Curvature Raceline Planning via Probabilistic Inference

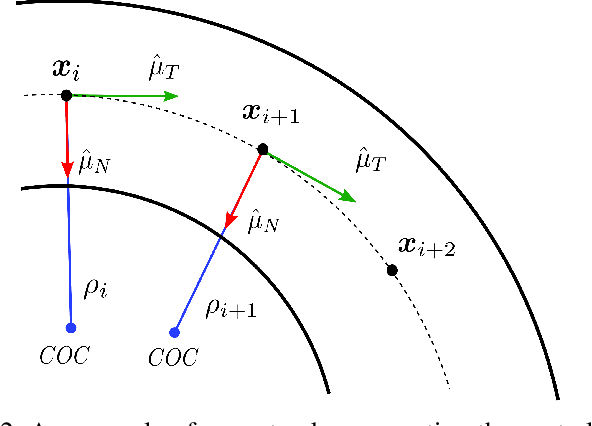
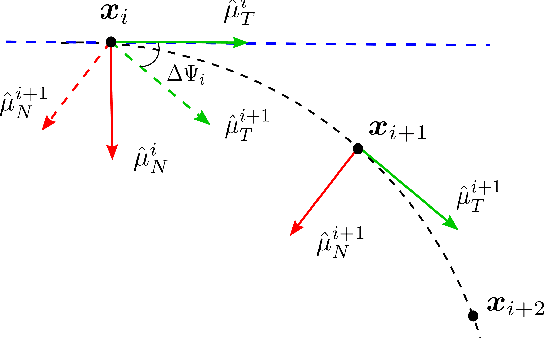
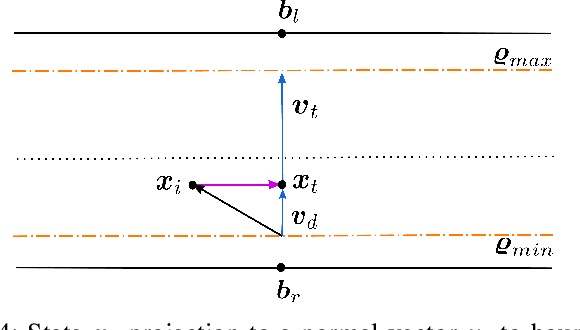
Finding a racing path that allows minimum lap time is the first and foremost step in overall autonomous race car planning. Minimum curvature path is the raceline that offers the highest cornering speed resulting in improved lap time for a given racetrack. Unfortunately, solving the geometrical optimization problem for finding a raceline is computationally expensive. In a competitive race, a few seconds difference in raceline computation could prove to be decisive. This paper presents a novel approach for finding the minimum curvature raceline via probabilistic inference. We leverage the tangential geometry and structure in the minimum curvature planning problem to formulate it on a factor graph, which is then solved as sparse non-linear least squares leading to a much faster algorithm. The proposed framework is evaluated for different racetracks and benchmark results are presented highlighting the computational efficiency, lap time and resulting raceline. Initial results indicate the viability of the proposed approach as it offers comparable lap time achievement with approximately four times faster computation time.

MS2MP: A Min-Sum Message Passing Algorithm for Motion Planning

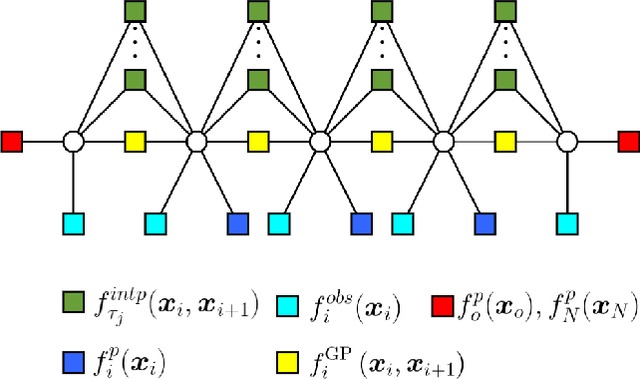
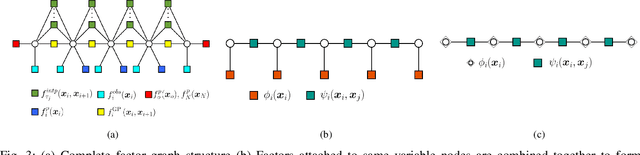
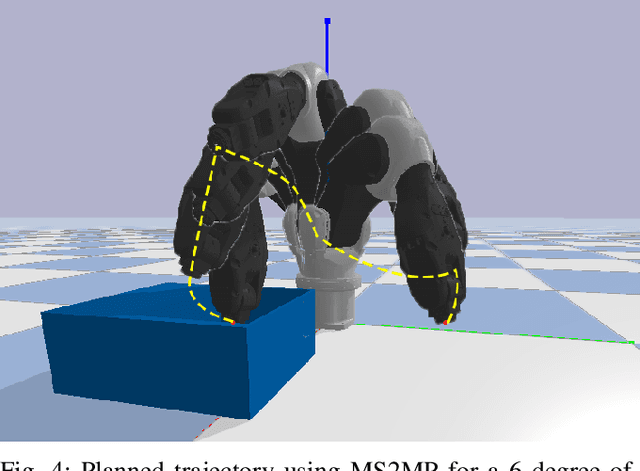
Gaussian Process (GP) formulation of continuoustime trajectory offers a fast solution to the motion planning problem via probabilistic inference on factor graph. However, often the solution converges to in-feasible local minima and the planned trajectory is not collision-free. We propose a message passing algorithm that is more sensitive to obstacles with fast convergence time. We leverage the utility of min-sum message passing algorithm that performs local computations at each node to solve the inference problem on factor graph. We first introduce the notion of compound factor node to transform the factor graph to a linearly structured graph. We next develop an algorithm denoted as Min-sum Message Passing algorithm for Motion Planning (MS2MP) that combines numerical optimization with message passing to find collision-free trajectories. MS2MP performs numerical optimization to solve non-linear least square minimization problem at each compound factor node and then exploits the linear structure of factor graph to compute the maximum a posteriori (MAP) estimation of complete graph by passing messages among graph nodes. The decentralized optimization approach of each compound node increases sensitivity towards avoiding obstacles for harder planning problems. We evaluate our algorithm by performing extensive experiments for exemplary motion planning tasks for a robot manipulator. Our evaluation reveals that MS2MP improves existing work in convergence time and success rate.