A Fast Approach to Minimum Curvature Raceline Planning via Probabilistic Inference

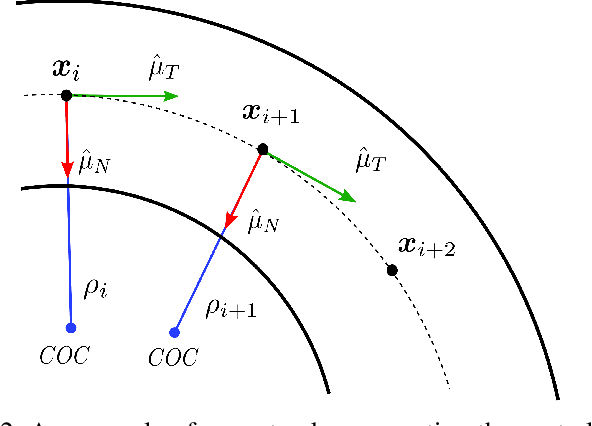
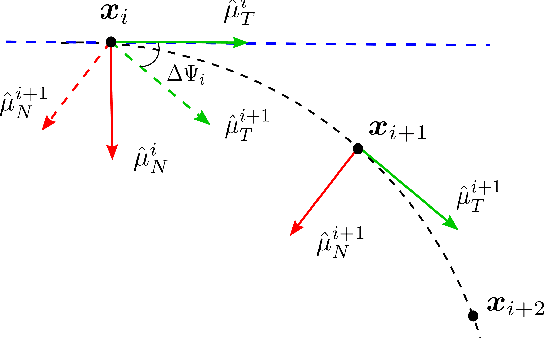
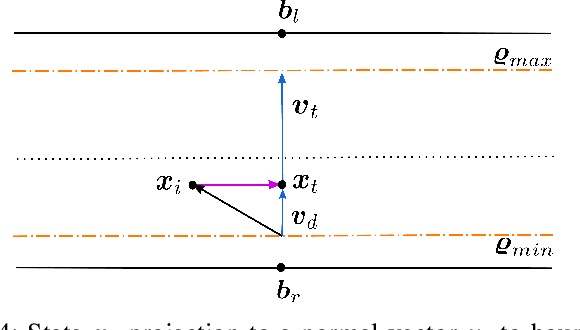
Finding a racing path that allows minimum lap time is the first and foremost step in overall autonomous race car planning. Minimum curvature path is the raceline that offers the highest cornering speed resulting in improved lap time for a given racetrack. Unfortunately, solving the geometrical optimization problem for finding a raceline is computationally expensive. In a competitive race, a few seconds difference in raceline computation could prove to be decisive. This paper presents a novel approach for finding the minimum curvature raceline via probabilistic inference. We leverage the tangential geometry and structure in the minimum curvature planning problem to formulate it on a factor graph, which is then solved as sparse non-linear least squares leading to a much faster algorithm. The proposed framework is evaluated for different racetracks and benchmark results are presented highlighting the computational efficiency, lap time and resulting raceline. Initial results indicate the viability of the proposed approach as it offers comparable lap time achievement with approximately four times faster computation time.