Learning Geometrically-Informed Lyapunov Functions with Deep Diffeomorphic RBF Networks

The practical deployment of learning-based autonomous systems would greatly benefit from tools that flexibly obtain safety guarantees in the form of certificate functions from data. While the geometrical properties of such certificate functions are well understood, synthesizing them using machine learning techniques still remains a challenge. To mitigate this issue, we propose a diffeomorphic function learning framework where prior structural knowledge of the desired output is encoded in the geometry of a simple surrogate function, which is subsequently augmented through an expressive, topology-preserving state-space transformation. Thereby, we achieve an indirect function approximation framework that is guaranteed to remain in the desired hypothesis space. To this end, we introduce a novel approach to construct diffeomorphic maps based on RBF networks, which facilitate precise, local transformations around data. Finally, we demonstrate our approach by learning diffeomorphic Lyapunov functions from real-world data and apply our method to different attractor systems.

Barrier Certificates for Unknown Systems with Latent States and Polynomial Dynamics using Bayesian Inference

Certifying safety in dynamical systems is crucial, but barrier certificates - widely used to verify that system trajectories remain within a safe region - typically require explicit system models. When dynamics are unknown, data-driven methods can be used instead, yet obtaining a valid certificate requires rigorous uncertainty quantification. For this purpose, existing methods usually rely on full-state measurements, limiting their applicability. This paper proposes a novel approach for synthesizing barrier certificates for unknown systems with latent states and polynomial dynamics. A Bayesian framework is employed, where a prior in state-space representation is updated using input-output data via a targeted marginal Metropolis-Hastings sampler. The resulting samples are used to construct a candidate barrier certificate through a sum-of-squares program. It is shown that if the candidate satisfies the required conditions on a test set of additional samples, it is also valid for the true, unknown system with high probability. The approach and its probabilistic guarantees are illustrated through a numerical simulation.

Koopman-Equivariant Gaussian Processes

Credible forecasting and representation learning of dynamical systems are of ever-increasing importance for reliable decision-making. To that end, we propose a family of Gaussian processes (GP) for dynamical systems with linear time-invariant responses, which are nonlinear only in initial conditions. This linearity allows us to tractably quantify forecasting and representational uncertainty, simultaneously alleviating the challenge of computing the distribution of trajectories from a GP-based dynamical system and enabling a new probabilistic treatment of learning Koopman operator representations. Using a trajectory-based equivariance -- which we refer to as \textit{Koopman equivariance} -- we obtain a GP model with enhanced generalization capabilities. To allow for large-scale regression, we equip our framework with variational inference based on suitable inducing points. Experiments demonstrate on-par and often better forecasting performance compared to kernel-based methods for learning dynamical systems.

Asynchronous Distributed Gaussian Process Regression for Online Learning and Dynamical Systems: Complementary Document

This is a complementary document for the paper titled "Asynchronous Distributed Gaussian Process Regression for Online Learning and Dynamical Systems".

Kernel-Based Optimal Control: An Infinitesimal Generator Approach

This paper presents a novel approach for optimal control of nonlinear stochastic systems using infinitesimal generator learning within infinite-dimensional reproducing kernel Hilbert spaces. Our learning framework leverages data samples of system dynamics and stage cost functions, with only control penalties and constraints provided. The proposed method directly learns the diffusion operator of a controlled Fokker-Planck-Kolmogorov equation in an infinite-dimensional hypothesis space. This operator models the continuous-time evolution of the probability measure of the control system's state. We demonstrate that this approach seamlessly integrates with modern convex operator-theoretic Hamilton-Jacobi-Bellman recursions, enabling a data-driven solution to the optimal control problem. Furthermore, our statistical learning framework includes nonparametric estimators for uncontrolled forward infinitesimal generators as a special case. Numerical experiments, ranging from synthetic differential equations to simulated robotic systems, showcase the advantages of our approach compared to both modern data-driven and classical nonlinear programming methods for optimal control.

Risk-averse learning with delayed feedback

In real-world scenarios, the impacts of decisions may not manifest immediately. Taking these delays into account facilitates accurate assessment and management of risk in real-world environments, thereby ensuring the efficacy of strategies. In this paper, we investigate risk-averse learning using Conditional Value at Risk (CVaR) as risk measure, while incorporating delayed feedback with unknown but bounded delays. We develop two risk-averse learning algorithms that rely on one-point and two-point zeroth-order optimization approaches, respectively. The regret achieved by the algorithms is analyzed in terms of the cumulative delay and the number of total samplings. The results suggest that the two-point risk-averse learning achieves a smaller regret bound than the one-point algorithm. Furthermore, the one-point risk-averse learning algorithm attains sublinear regret under certain delay conditions, and the two-point risk-averse learning algorithm achieves sublinear regret with minimal restrictions on the delay. We provide numerical experiments on a dynamic pricing problem to demonstrate the performance of the proposed algorithms.

Reinforcement Learning with Lie Group Orientations for Robotics

Handling orientations of robots and objects is a crucial aspect of many applications. Yet, ever so often, there is a lack of mathematical correctness when dealing with orientations, especially in learning pipelines involving, for example, artificial neural networks. In this paper, we investigate reinforcement learning with orientations and propose a simple modification of the network's input and output that adheres to the Lie group structure of orientations. As a result, we obtain an easy and efficient implementation that is directly usable with existing learning libraries and achieves significantly better performance than other common orientation representations. We briefly introduce Lie theory specifically for orientations in robotics to motivate and outline our approach. Subsequently, a thorough empirical evaluation of different combinations of orientation representations for states and actions demonstrates the superior performance of our proposed approach in different scenarios, including: direct orientation control, end effector orientation control, and pick-and-place tasks.

Jacta: A Versatile Planner for Learning Dexterous and Whole-body Manipulation

Robotic manipulation is challenging due to discontinuous dynamics, as well as high-dimensional state and action spaces. Data-driven approaches that succeed in manipulation tasks require large amounts of data and expert demonstrations, typically from humans. Existing manipulation planners are restricted to specific systems and often depend on specialized algorithms for using demonstration. Therefore, we introduce a flexible motion planner tailored to dexterous and whole-body manipulation tasks. Our planner creates readily usable demonstrations for reinforcement learning algorithms, eliminating the need for additional training pipeline complexities. With this approach, we can efficiently learn policies for complex manipulation tasks, where traditional reinforcement learning alone only makes little progress. Furthermore, we demonstrate that learned policies are transferable to real robotic systems for solving complex dexterous manipulation tasks.

Autonomous and Teleoperation Control of a Drawing Robot Avatar

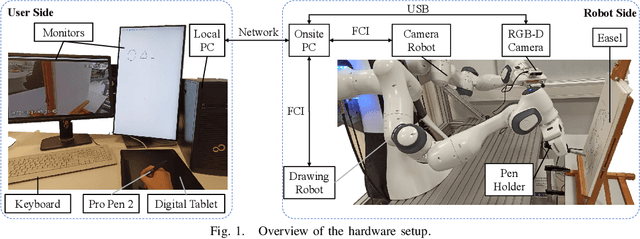
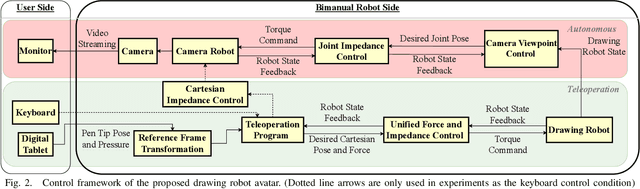
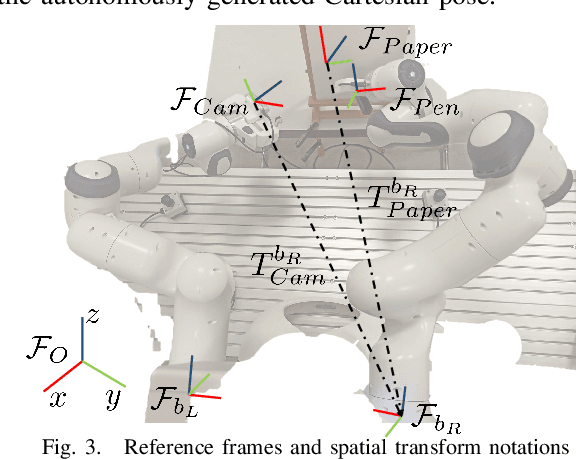
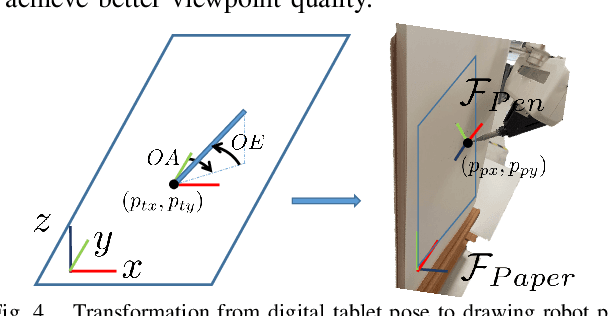
A drawing robot avatar is a robotic system that allows for telepresence-based drawing, enabling users to remotely control a robotic arm and create drawings in real-time from a remote location. The proposed control framework aims to improve bimanual robot telepresence quality by reducing the user workload and required prior knowledge through the automation of secondary or auxiliary tasks. The introduced novel method calculates the near-optimal Cartesian end-effector pose in terms of visual feedback quality for the attached eye-to-hand camera with motion constraints in consideration. The effectiveness is demonstrated by conducting user studies of drawing reference shapes using the implemented robot avatar compared to stationary and teleoperated camera pose conditions. Our results demonstrate that the proposed control framework offers improved visual feedback quality and drawing performance.

Data-Driven Optimal Feedback Laws via Kernel Mean Embeddings

This paper proposes a fully data-driven approach for optimal control of nonlinear control-affine systems represented by a stochastic diffusion. The focus is on the scenario where both the nonlinear dynamics and stage cost functions are unknown, while only control penalty function and constraints are provided. Leveraging the theory of reproducing kernel Hilbert spaces, we introduce novel kernel mean embeddings (KMEs) to identify the Markov transition operators associated with controlled diffusion processes. The KME learning approach seamlessly integrates with modern convex operator-theoretic Hamilton-Jacobi-Bellman recursions. Thus, unlike traditional dynamic programming methods, our approach exploits the ``kernel trick'' to break the curse of dimensionality. We demonstrate the effectiveness of our method through numerical examples, highlighting its ability to solve a large class of nonlinear optimal control problems.