Token-Level Logits Matter: A Closer Look at Speech Foundation Models for Ambiguous Emotion Recognition

Emotional intelligence in conversational AI is crucial across domains like human-computer interaction. While numerous models have been developed, they often overlook the complexity and ambiguity inherent in human emotions. In the era of large speech foundation models (SFMs), understanding their capability in recognizing ambiguous emotions is essential for the development of next-generation emotion-aware models. This study examines the effectiveness of SFMs in ambiguous emotion recognition. We designed prompts for ambiguous emotion prediction and introduced two novel approaches to infer ambiguous emotion distributions: one analysing generated text responses and the other examining the internal processing of SFMs through token-level logits. Our findings suggest that while SFMs may not consistently generate accurate text responses for ambiguous emotions, they can interpret such emotions at the token level based on prior knowledge, demonstrating robustness across different prompts.

Depth-Based Local Center Clustering: A Framework for Handling Different Clustering Scenarios

Cluster analysis, or clustering, plays a crucial role across numerous scientific and engineering domains. Despite the wealth of clustering methods proposed over the past decades, each method is typically designed for specific scenarios and presents certain limitations in practical applications. In this paper, we propose depth-based local center clustering (DLCC). This novel method makes use of data depth, which is known to produce a center-outward ordering of sample points in a multivariate space. However, data depth typically fails to capture the multimodal characteristics of {data}, something of the utmost importance in the context of clustering. To overcome this, DLCC makes use of a local version of data depth that is based on subsets of {data}. From this, local centers can be identified as well as clusters of varying shapes. Furthermore, we propose a new internal metric based on density-based clustering to evaluate clustering performance on {non-convex clusters}. Overall, DLCC is a flexible clustering approach that seems to overcome some limitations of traditional clustering methods, thereby enhancing data analysis capabilities across a wide range of application scenarios.

An Investigation into Value Misalignment in LLM-Generated Texts for Cultural Heritage

As Large Language Models (LLMs) become increasingly prevalent in tasks related to cultural heritage, such as generating descriptions of historical monuments, translating ancient texts, preserving oral traditions, and creating educational content, their ability to produce accurate and culturally aligned texts is being increasingly relied upon by users and researchers. However, cultural value misalignments may exist in generated texts, such as the misrepresentation of historical facts, the erosion of cultural identity, and the oversimplification of complex cultural narratives, which may lead to severe consequences. Therefore, investigating value misalignment in the context of LLM for cultural heritage is crucial for mitigating these risks, yet there has been a significant lack of systematic and comprehensive study and investigation in this area. To fill this gap, we systematically assess the reliability of LLMs in generating culturally aligned texts for cultural heritage-related tasks. We conduct a comprehensive evaluation by compiling an extensive set of 1066 query tasks covering 5 widely recognized categories with 17 aspects within the knowledge framework of cultural heritage across 5 open-source LLMs, and examine both the type and rate of cultural value misalignments in the generated texts. Using both automated and manual approaches, we effectively detect and analyze the cultural value misalignments in LLM-generated texts. Our findings are concerning: over 65% of the generated texts exhibit notable cultural misalignments, with certain tasks demonstrating almost complete misalignment with key cultural values. Beyond these findings, this paper introduces a benchmark dataset and a comprehensive evaluation workflow that can serve as a valuable resource for future research aimed at enhancing the cultural sensitivity and reliability of LLMs.

Risk-averse learning with delayed feedback

In real-world scenarios, the impacts of decisions may not manifest immediately. Taking these delays into account facilitates accurate assessment and management of risk in real-world environments, thereby ensuring the efficacy of strategies. In this paper, we investigate risk-averse learning using Conditional Value at Risk (CVaR) as risk measure, while incorporating delayed feedback with unknown but bounded delays. We develop two risk-averse learning algorithms that rely on one-point and two-point zeroth-order optimization approaches, respectively. The regret achieved by the algorithms is analyzed in terms of the cumulative delay and the number of total samplings. The results suggest that the two-point risk-averse learning achieves a smaller regret bound than the one-point algorithm. Furthermore, the one-point risk-averse learning algorithm attains sublinear regret under certain delay conditions, and the two-point risk-averse learning algorithm achieves sublinear regret with minimal restrictions on the delay. We provide numerical experiments on a dynamic pricing problem to demonstrate the performance of the proposed algorithms.

Diffusion-based Speech Enhancement with Schrödinger Bridge and Symmetric Noise Schedule

Recently, diffusion-based generative models have demonstrated remarkable performance in speech enhancement tasks. However, these methods still encounter challenges, including the lack of structural information and poor performance in low Signal-to-Noise Ratio (SNR) scenarios. To overcome these challenges, we propose the Schr\"oodinger Bridge-based Speech Enhancement (SBSE) method, which learns the diffusion processes directly between the noisy input and the clean distribution, unlike conventional diffusion-based speech enhancement systems that learn data to Gaussian distributions. To enhance performance in extremely noisy conditions, we introduce a two-stage system incorporating ratio mask information into the diffusion-based generative model. Our experimental results show that our proposed SBSE method outperforms all the baseline models and achieves state-of-the-art performance, especially in low SNR conditions. Importantly, only a few inference steps are required to achieve the best result.

Efficient Quantum Circuits for Machine Learning Activation Functions including Constant T-depth ReLU

In recent years, Quantum Machine Learning (QML) has increasingly captured the interest of researchers. Among the components in this domain, activation functions hold a fundamental and indispensable role. Our research focuses on the development of activation functions quantum circuits for integration into fault-tolerant quantum computing architectures, with an emphasis on minimizing $T$-depth. Specifically, we present novel implementations of ReLU and leaky ReLU activation functions, achieving constant $T$-depths of 4 and 8, respectively. Leveraging quantum lookup tables, we extend our exploration to other activation functions such as the sigmoid. This approach enables us to customize precision and $T$-depth by adjusting the number of qubits, making our results more adaptable to various application scenarios. This study represents a significant advancement towards enhancing the practicality and application of quantum machine learning.

Risk-averse Learning with Non-Stationary Distributions

Considering non-stationary environments in online optimization enables decision-maker to effectively adapt to changes and improve its performance over time. In such cases, it is favorable to adopt a strategy that minimizes the negative impact of change to avoid potentially risky situations. In this paper, we investigate risk-averse online optimization where the distribution of the random cost changes over time. We minimize risk-averse objective function using the Conditional Value at Risk (CVaR) as risk measure. Due to the difficulty in obtaining the exact CVaR gradient, we employ a zeroth-order optimization approach that queries the cost function values multiple times at each iteration and estimates the CVaR gradient using the sampled values. To facilitate the regret analysis, we use a variation metric based on Wasserstein distance to capture time-varying distributions. Given that the distribution variation is sub-linear in the total number of episodes, we show that our designed learning algorithm achieves sub-linear dynamic regret with high probability for both convex and strongly convex functions. Moreover, theoretical results suggest that increasing the number of samples leads to a reduction in the dynamic regret bounds until the sampling number reaches a specific limit. Finally, we provide numerical experiments of dynamic pricing in a parking lot to illustrate the efficacy of the designed algorithm.

Unveiling the Potential of Robustness in Evaluating Causal Inference Models

The growing demand for personalized decision-making has led to a surge of interest in estimating the Conditional Average Treatment Effect (CATE). The intersection of machine learning and causal inference has yielded various effective CATE estimators. However, deploying these estimators in practice is often hindered by the absence of counterfactual labels, making it challenging to select the desirable CATE estimator using conventional model selection procedures like cross-validation. Existing approaches for CATE estimator selection, such as plug-in and pseudo-outcome metrics, face two inherent challenges. Firstly, they are required to determine the metric form and the underlying machine learning models for fitting nuisance parameters or plug-in learners. Secondly, they lack a specific focus on selecting a robust estimator. To address these challenges, this paper introduces a novel approach, the Distributionally Robust Metric (DRM), for CATE estimator selection. The proposed DRM not only eliminates the need to fit additional models but also excels at selecting a robust CATE estimator. Experimental studies demonstrate the efficacy of the DRM method, showcasing its consistent effectiveness in identifying superior estimators while mitigating the risk of selecting inferior ones.

Multimodal Short Video Rumor Detection System Based on Contrastive Learning

With short video platforms becoming one of the important channels for news sharing, major short video platforms in China have gradually become new breeding grounds for fake news. However, it is not easy to distinguish short video rumors due to the great amount of information and features contained in short videos, as well as the serious homogenization and similarity of features among videos. In order to mitigate the spread of short video rumors, our group decides to detect short video rumors by constructing multimodal feature fusion and introducing external knowledge after considering the advantages and disadvantages of each algorithm. The ideas of detection are as follows: (1) dataset creation: to build a short video dataset with multiple features; (2) multimodal rumor detection model: firstly, we use TSN (Temporal Segment Networks) video coding model to extract video features; then, we use OCR (Optical Character Recognition) and ASR (Automatic Character Recognition) to extract video features. Recognition) and ASR (Automatic Speech Recognition) fusion to extract text, and then use the BERT model to fuse text features with video features (3) Finally, use contrast learning to achieve distinction: first crawl external knowledge, then use the vector database to achieve the introduction of external knowledge and the final structure of the classification output. Our research process is always oriented to practical needs, and the related knowledge results will play an important role in many practical scenarios such as short video rumor identification and social opinion control.

Policy Evaluation in Distributional LQR

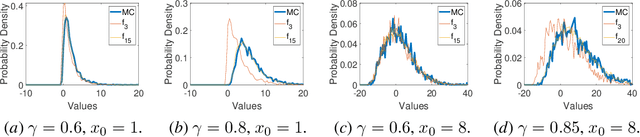
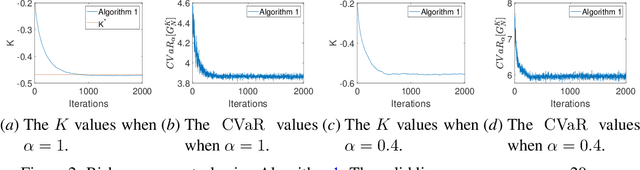
Distributional reinforcement learning (DRL) enhances the understanding of the effects of the randomness in the environment by letting agents learn the distribution of a random return, rather than its expected value as in standard RL. At the same time, a main challenge in DRL is that policy evaluation in DRL typically relies on the representation of the return distribution, which needs to be carefully designed. In this paper, we address this challenge for a special class of DRL problems that rely on linear quadratic regulator (LQR) for control, advocating for a new distributional approach to LQR, which we call \emph{distributional LQR}. Specifically, we provide a closed-form expression of the distribution of the random return which, remarkably, is applicable to all exogenous disturbances on the dynamics, as long as they are independent and identically distributed (i.i.d.). While the proposed exact return distribution consists of infinitely many random variables, we show that this distribution can be approximated by a finite number of random variables, and the associated approximation error can be analytically bounded under mild assumptions. Using the approximate return distribution, we propose a zeroth-order policy gradient algorithm for risk-averse LQR using the Conditional Value at Risk (CVaR) as a measure of risk. Numerical experiments are provided to illustrate our theoretical results.