Source-Guided Flow Matching

Guidance of generative models is typically achieved by modifying the probability flow vector field through the addition of a guidance field. In this paper, we instead propose the Source-Guided Flow Matching (SGFM) framework, which modifies the source distribution directly while keeping the pre-trained vector field intact. This reduces the guidance problem to a well-defined problem of sampling from the source distribution. We theoretically show that SGFM recovers the desired target distribution exactly. Furthermore, we provide bounds on the Wasserstein error for the generated distribution when using an approximate sampler of the source distribution and an approximate vector field. The key benefit of our approach is that it allows the user to flexibly choose the sampling method depending on their specific problem. To illustrate this, we systematically compare different sampling methods and discuss conditions for asymptotically exact guidance. Moreover, our framework integrates well with optimal flow matching models since the straight transport map generated by the vector field is preserved. Experimental results on synthetic 2D benchmarks, image datasets, and physics-informed generative tasks demonstrate the effectiveness and flexibility of the proposed framework.

Beyond Line-of-Sight: Cooperative Localization Using Vision and V2X Communication

Accurate and robust localization is critical for the safe operation of Connected and Automated Vehicles (CAVs), especially in complex urban environments where Global Navigation Satellite System (GNSS) signals are unreliable. This paper presents a novel vision-based cooperative localization algorithm that leverages onboard cameras and Vehicle-to-Everything (V2X) communication to enable CAVs to estimate their poses, even in occlusion-heavy scenarios such as busy intersections. In particular, we propose a novel decentralized observer for a group of connected agents that includes landmark agents (static or moving) in the environment with known positions and vehicle agents that need to estimate their poses (both positions and orientations). Assuming that (i) there are at least three landmark agents in the environment, (ii) each vehicle agent can measure its own angular and translational velocities as well as relative bearings to at least three neighboring landmarks or vehicles, and (iii) neighboring vehicles can communicate their pose estimates, each vehicle can estimate its own pose using the proposed decentralized observer. We prove that the origin of the estimation error is locally exponentially stable under the proposed observer, provided that the minimal observability conditions are satisfied. Moreover, we evaluate the proposed approach through experiments with real 1/10th-scale connected vehicles and large-scale simulations, demonstrating its scalability and validating the theoretical guarantees in practical scenarios.

Personalized and Resilient Distributed Learning Through Opinion Dynamics

In this paper, we address two practical challenges of distributed learning in multi-agent network systems, namely personalization and resilience. Personalization is the need of heterogeneous agents to learn local models tailored to their own data and tasks, while still generalizing well; on the other hand, the learning process must be resilient to cyberattacks or anomalous training data to avoid disruption. Motivated by a conceptual affinity between these two requirements, we devise a distributed learning algorithm that combines distributed gradient descent and the Friedkin-Johnsen model of opinion dynamics to fulfill both of them. We quantify its convergence speed and the neighborhood that contains the final learned models, which can be easily controlled by tuning the algorithm parameters to enforce a more personalized/resilient behavior. We numerically showcase the effectiveness of our algorithm on synthetic and real-world distributed learning tasks, where it achieves high global accuracy both for personalized models and with malicious agents compared to standard strategies.

A Centralized Planning and Distributed Execution Method for Shape Filling with Homogeneous Mobile Robots

Nature has inspired humans in different ways. The formation behavior of animals can perform tasks that exceed individual capability. For example, army ants could transverse gaps by forming bridges, and fishes could group up to protect themselves from predators. The pattern formation task is essential in a multiagent robotic system because it usually serves as the initial configuration of downstream tasks, such as collective manipulation and adaptation to various environments. The formation of complex shapes, especially hollow shapes, remains an open question. Traditional approaches either require global coordinates for each robot or are prone to failure when attempting to close the hole due to accumulated localization errors. Inspired by the ribbon idea introduced in the additive self-assembly algorithm by the Kilobot team, we develop a two-stage algorithm that does not require global coordinates information and effectively forms shapes with holes. In this paper, we investigate the partitioning of the shape using ribbons in a hexagonal lattice setting and propose the add-subtract algorithm based on the movement sequence induced by the ribbon structure. This advancement opens the door to tasks requiring complex pattern formations, such as the assembly of nanobots for medical applications involving intricate structures and the deployment of robots along the boundaries of areas of interest. We also provide simulation results on complex shapes, an analysis of the robustness as well as a proof of correctness of the proposed algorithm.

Optimization and Learning in Open Multi-Agent Systems

Modern artificial intelligence relies on networks of agents that collect data, process information, and exchange it with neighbors to collaboratively solve optimization and learning problems. This article introduces a novel distributed algorithm to address a broad class of these problems in "open networks", where the number of participating agents may vary due to several factors, such as autonomous decisions, heterogeneous resource availability, or DoS attacks. Extending the current literature, the convergence analysis of the proposed algorithm is based on the newly developed "Theory of Open Operators", which characterizes an operator as open when the set of components to be updated changes over time, yielding to time-varying operators acting on sequences of points of different dimensions and compositions. The mathematical tools and convergence results developed here provide a general framework for evaluating distributed algorithms in open networks, allowing to characterize their performance in terms of the punctual distance from the optimal solution, in contrast with regret-based metrics that assess cumulative performance over a finite-time horizon. As illustrative examples, the proposed algorithm is used to solve dynamic consensus or tracking problems on different metrics of interest, such as average, median, and min/max value, as well as classification problems with logistic loss functions.

Hierarchical Federated ADMM

In this paper, we depart from the widely-used gradient descent-based hierarchical federated learning (FL) algorithms to develop a novel hierarchical FL framework based on the alternating direction method of multipliers (ADMM). Within this framework, we propose two novel FL algorithms, which both use ADMM in the top layer: one that employs ADMM in the lower layer and another that uses the conventional gradient descent-based approach. The proposed framework enhances privacy, and experiments demonstrate the superiority of the proposed algorithms compared to the conventional algorithms in terms of learning convergence and accuracy. Additionally, gradient descent on the lower layer performs well even if the number of local steps is very limited, while ADMM on both layers lead to better performance otherwise.

Byzantine-Robust and Communication-Efficient Distributed Learning via Compressed Momentum Filtering

Distributed learning has become the standard approach for training large-scale machine learning models across private data silos. While distributed learning enhances privacy preservation and training efficiency, it faces critical challenges related to Byzantine robustness and communication reduction. Existing Byzantine-robust and communication-efficient methods rely on full gradient information either at every iteration or at certain iterations with a probability, and they only converge to an unnecessarily large neighborhood around the solution. Motivated by these issues, we propose a novel Byzantine-robust and communication-efficient stochastic distributed learning method that imposes no requirements on batch size and converges to a smaller neighborhood around the optimal solution than all existing methods, aligning with the theoretical lower bound. Our key innovation is leveraging Polyak Momentum to mitigate the noise caused by both biased compressors and stochastic gradients, thus defending against Byzantine workers under information compression. We provide proof of tight complexity bounds for our algorithm in the context of non-convex smooth loss functions, demonstrating that these bounds match the lower bounds in Byzantine-free scenarios. Finally, we validate the practical significance of our algorithm through an extensive series of experiments, benchmarking its performance on both binary classification and image classification tasks.

A survey on secure decentralized optimization and learning

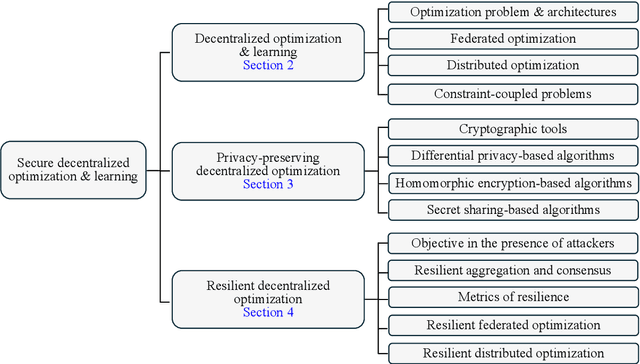
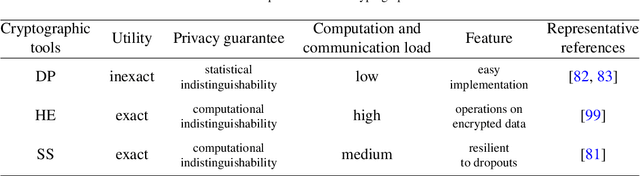
Decentralized optimization has become a standard paradigm for solving large-scale decision-making problems and training large machine learning models without centralizing data. However, this paradigm introduces new privacy and security risks, with malicious agents potentially able to infer private data or impair the model accuracy. Over the past decade, significant advancements have been made in developing secure decentralized optimization and learning frameworks and algorithms. This survey provides a comprehensive tutorial on these advancements. We begin with the fundamentals of decentralized optimization and learning, highlighting centralized aggregation and distributed consensus as key modules exposed to security risks in federated and distributed optimization, respectively. Next, we focus on privacy-preserving algorithms, detailing three cryptographic tools and their integration into decentralized optimization and learning systems. Additionally, we examine resilient algorithms, exploring the design and analysis of resilient aggregation and consensus protocols that support these systems. We conclude the survey by discussing current trends and potential future directions.

A Differential Dynamic Programming Framework for Inverse Reinforcement Learning

A differential dynamic programming (DDP)-based framework for inverse reinforcement learning (IRL) is introduced to recover the parameters in the cost function, system dynamics, and constraints from demonstrations. Different from existing work, where DDP was used for the inner forward problem with inequality constraints, our proposed framework uses it for efficient computation of the gradient required in the outer inverse problem with equality and inequality constraints. The equivalence between the proposed method and existing methods based on Pontryagin's Maximum Principle (PMP) is established. More importantly, using this DDP-based IRL with an open-loop loss function, a closed-loop IRL framework is presented. In this framework, a loss function is proposed to capture the closed-loop nature of demonstrations. It is shown to be better than the commonly used open-loop loss function. We show that the closed-loop IRL framework reduces to a constrained inverse optimal control problem under certain assumptions. Under these assumptions and a rank condition, it is proven that the learning parameters can be recovered from the demonstration data. The proposed framework is extensively evaluated through four numerical robot examples and one real-world quadrotor system. The experiments validate the theoretical results and illustrate the practical relevance of the approach.

Ensuring Safety at Intelligent Intersections: Temporal Logic Meets Reachability Analysis

In this work, we propose an approach for ensuring the safety of vehicles passing through an intelligent intersection. There are many proposals for the design of intelligent intersections that introduce central decision-makers to intersections for enhancing the efficiency and safety of the vehicles. To guarantee the safety of such designs, we develop a safety framework for intersections based on temporal logic and reachability analysis. We start by specifying the required behavior for all the vehicles that need to pass through the intersection as linear temporal logic formula. Then, using temporal logic trees, we break down the linear temporal logic specification into a series of Hamilton-Jacobi reachability analyses in an automated fashion. By successfully constructing the temporal logic tree through reachability analysis, we verify the feasibility of the intersection specification. By taking this approach, we enable a safety framework that is able to automatically provide safety guarantees on new intersection behavior specifications. To evaluate our approach, we implement the framework on a simulated T-intersection, where we show that we can check and guarantee the safety of vehicles with potentially conflicting paths.