Optimization and Learning in Open Multi-Agent Systems

Modern artificial intelligence relies on networks of agents that collect data, process information, and exchange it with neighbors to collaboratively solve optimization and learning problems. This article introduces a novel distributed algorithm to address a broad class of these problems in "open networks", where the number of participating agents may vary due to several factors, such as autonomous decisions, heterogeneous resource availability, or DoS attacks. Extending the current literature, the convergence analysis of the proposed algorithm is based on the newly developed "Theory of Open Operators", which characterizes an operator as open when the set of components to be updated changes over time, yielding to time-varying operators acting on sequences of points of different dimensions and compositions. The mathematical tools and convergence results developed here provide a general framework for evaluating distributed algorithms in open networks, allowing to characterize their performance in terms of the punctual distance from the optimal solution, in contrast with regret-based metrics that assess cumulative performance over a finite-time horizon. As illustrative examples, the proposed algorithm is used to solve dynamic consensus or tracking problems on different metrics of interest, such as average, median, and min/max value, as well as classification problems with logistic loss functions.

Online Distributed Learning over Random Networks

The recent deployment of multi-agent systems in a wide range of scenarios has enabled the solution of learning problems in a distributed fashion. In this context, agents are tasked with collecting local data and then cooperatively train a model, without directly sharing the data. While distributed learning offers the advantage of preserving agents' privacy, it also poses several challenges in terms of designing and analyzing suitable algorithms. This work focuses specifically on the following challenges motivated by practical implementation: (i) online learning, where the local data change over time; (ii) asynchronous agent computations; (iii) unreliable and limited communications; and (iv) inexact local computations. To tackle these challenges, we introduce the Distributed Operator Theoretical (DOT) version of the Alternating Direction Method of Multipliers (ADMM), which we call the DOT-ADMM Algorithm. We prove that it converges with a linear rate for a large class of convex learning problems (e.g., linear and logistic regression problems) toward a bounded neighborhood of the optimal time-varying solution, and characterize how the neighborhood depends on~$\text{(i)--(iv)}$. We corroborate the theoretical analysis with numerical simulations comparing the DOT-ADMM Algorithm with other state-of-the-art algorithms, showing that only the proposed algorithm exhibits robustness to (i)--(iv).

Consensus on the average in arbitrary directed network topologies with time-delays

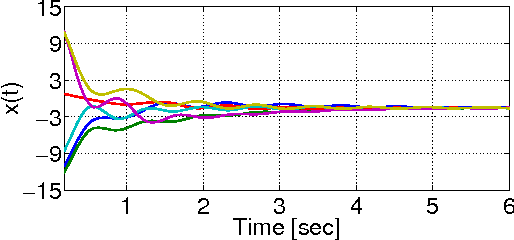
In this preliminary paper we study the stability property of a consensus on the average algorithm in arbitrary directed graphs with respect to communication/sensing time-delays. The proposed algorithm adds a storage variable to the agents' states so that the information about the average of the states is preserved despite the algorithm iterations are performed in an arbitrary strongly connected directed graph. We prove that for any network topology and choice of design parameters the consensus on the average algorithm is stable for sufficiently small delays. We provide simulations and numerical results to estimate the maximum delay allowed by an arbitrary unbalanced directed network topology.