Personalized and Resilient Distributed Learning Through Opinion Dynamics

In this paper, we address two practical challenges of distributed learning in multi-agent network systems, namely personalization and resilience. Personalization is the need of heterogeneous agents to learn local models tailored to their own data and tasks, while still generalizing well; on the other hand, the learning process must be resilient to cyberattacks or anomalous training data to avoid disruption. Motivated by a conceptual affinity between these two requirements, we devise a distributed learning algorithm that combines distributed gradient descent and the Friedkin-Johnsen model of opinion dynamics to fulfill both of them. We quantify its convergence speed and the neighborhood that contains the final learned models, which can be easily controlled by tuning the algorithm parameters to enforce a more personalized/resilient behavior. We numerically showcase the effectiveness of our algorithm on synthetic and real-world distributed learning tasks, where it achieves high global accuracy both for personalized models and with malicious agents compared to standard strategies.

Modular Distributed Nonconvex Learning with Error Feedback

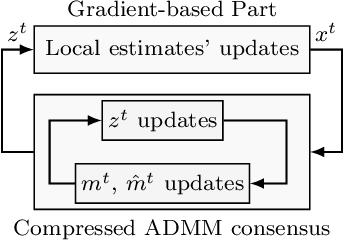
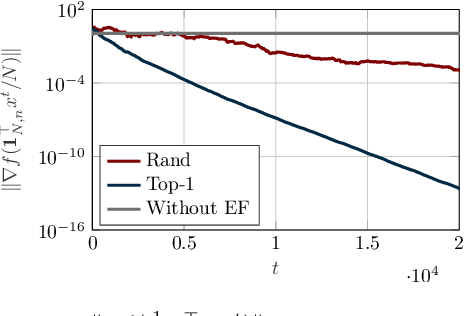
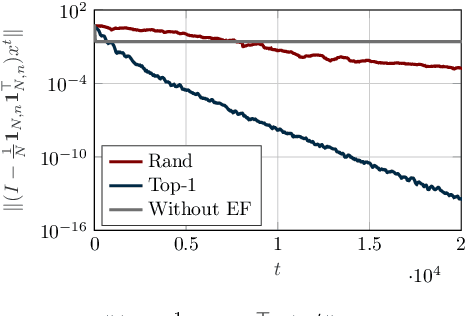
In this paper, we design a novel distributed learning algorithm using stochastic compressed communications. In detail, we pursue a modular approach, merging ADMM and a gradient-based approach, benefiting from the robustness of the former and the computational efficiency of the latter. Additionally, we integrate a stochastic integral action (error feedback) enabling almost sure rejection of the compression error. We analyze the resulting method in nonconvex scenarios and guarantee almost sure asymptotic convergence to the set of stationary points of the problem. This result is obtained using system-theoretic tools based on stochastic timescale separation. We corroborate our findings with numerical simulations in nonconvex classification.

Optimization and Learning in Open Multi-Agent Systems

Modern artificial intelligence relies on networks of agents that collect data, process information, and exchange it with neighbors to collaboratively solve optimization and learning problems. This article introduces a novel distributed algorithm to address a broad class of these problems in "open networks", where the number of participating agents may vary due to several factors, such as autonomous decisions, heterogeneous resource availability, or DoS attacks. Extending the current literature, the convergence analysis of the proposed algorithm is based on the newly developed "Theory of Open Operators", which characterizes an operator as open when the set of components to be updated changes over time, yielding to time-varying operators acting on sequences of points of different dimensions and compositions. The mathematical tools and convergence results developed here provide a general framework for evaluating distributed algorithms in open networks, allowing to characterize their performance in terms of the punctual distance from the optimal solution, in contrast with regret-based metrics that assess cumulative performance over a finite-time horizon. As illustrative examples, the proposed algorithm is used to solve dynamic consensus or tracking problems on different metrics of interest, such as average, median, and min/max value, as well as classification problems with logistic loss functions.

Hierarchical Federated ADMM

In this paper, we depart from the widely-used gradient descent-based hierarchical federated learning (FL) algorithms to develop a novel hierarchical FL framework based on the alternating direction method of multipliers (ADMM). Within this framework, we propose two novel FL algorithms, which both use ADMM in the top layer: one that employs ADMM in the lower layer and another that uses the conventional gradient descent-based approach. The proposed framework enhances privacy, and experiments demonstrate the superiority of the proposed algorithms compared to the conventional algorithms in terms of learning convergence and accuracy. Additionally, gradient descent on the lower layer performs well even if the number of local steps is very limited, while ADMM on both layers lead to better performance otherwise.

Learning and Verifying Maximal Taylor-Neural Lyapunov functions

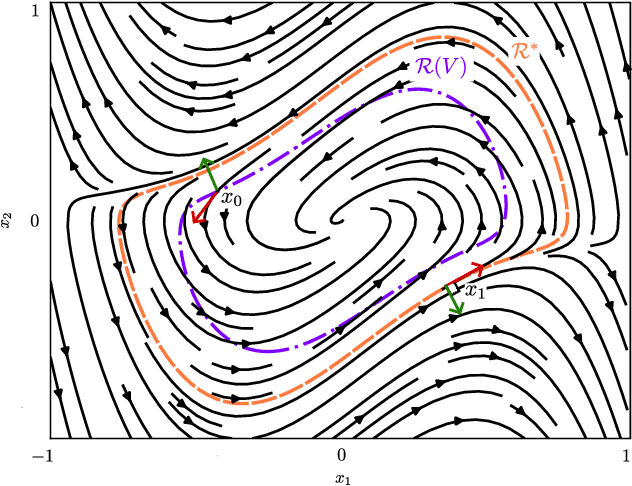
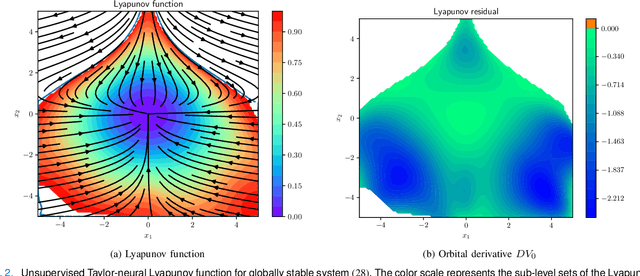
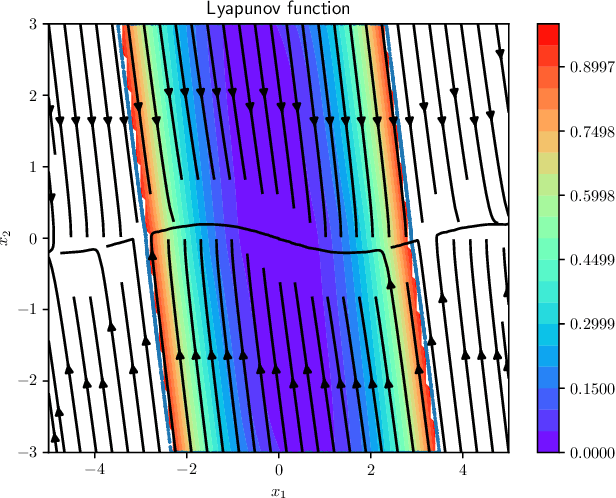
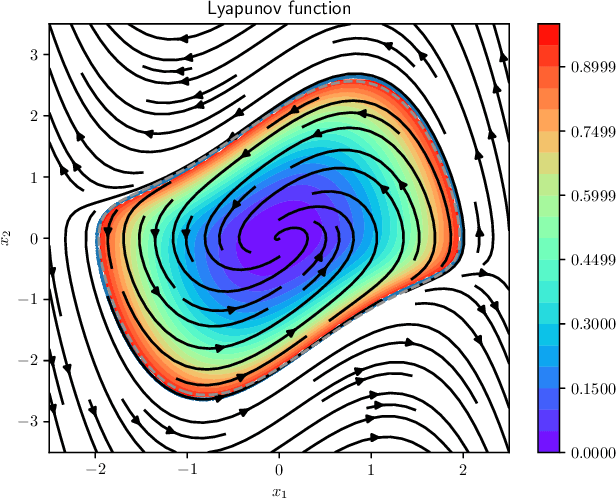
We introduce a novel neural network architecture, termed Taylor-neural Lyapunov functions, designed to approximate Lyapunov functions with formal certification. This architecture innovatively encodes local approximations and extends them globally by leveraging neural networks to approximate the residuals. Our method recasts the problem of estimating the largest region of attraction - specifically for maximal Lyapunov functions - into a learning problem, ensuring convergence around the origin through robust control theory. Physics-informed machine learning techniques further refine the estimation of the largest region of attraction. Remarkably, this method is versatile, operating effectively even without simulated data points. We validate the efficacy of our approach by providing numerical certificates of convergence across multiple examples. Our proposed methodology not only competes closely with state-of-the-art approaches, such as sum-of-squares and LyZNet, but also achieves comparable results even in the absence of simulated data. This work represents a significant advancement in control theory, with broad potential applications in the design of stable control systems and beyond.

A survey on secure decentralized optimization and learning

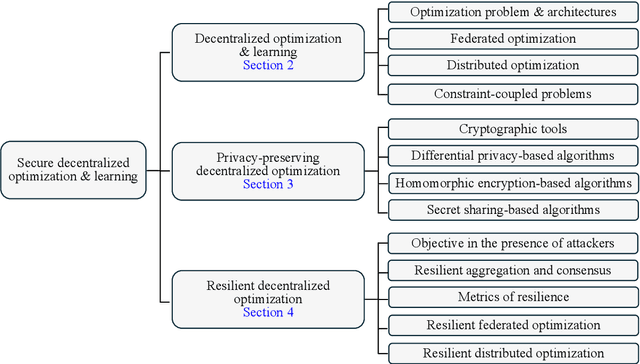
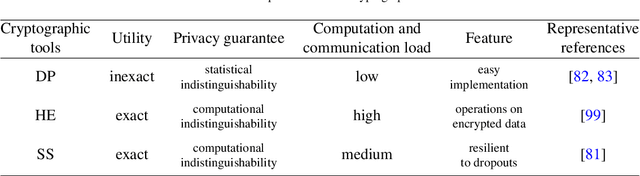
Decentralized optimization has become a standard paradigm for solving large-scale decision-making problems and training large machine learning models without centralizing data. However, this paradigm introduces new privacy and security risks, with malicious agents potentially able to infer private data or impair the model accuracy. Over the past decade, significant advancements have been made in developing secure decentralized optimization and learning frameworks and algorithms. This survey provides a comprehensive tutorial on these advancements. We begin with the fundamentals of decentralized optimization and learning, highlighting centralized aggregation and distributed consensus as key modules exposed to security risks in federated and distributed optimization, respectively. Next, we focus on privacy-preserving algorithms, detailing three cryptographic tools and their integration into decentralized optimization and learning systems. Additionally, we examine resilient algorithms, exploring the design and analysis of resilient aggregation and consensus protocols that support these systems. We conclude the survey by discussing current trends and potential future directions.

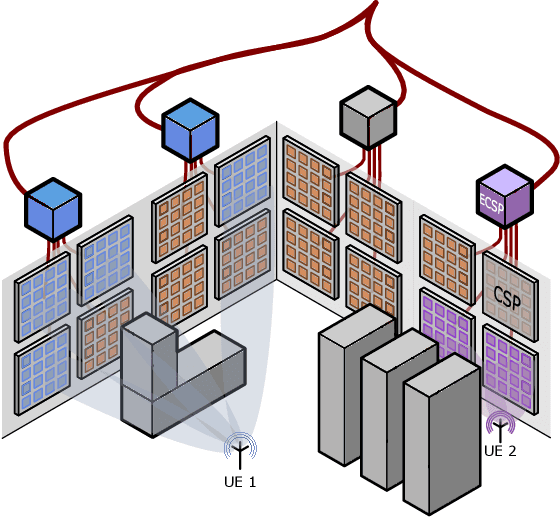
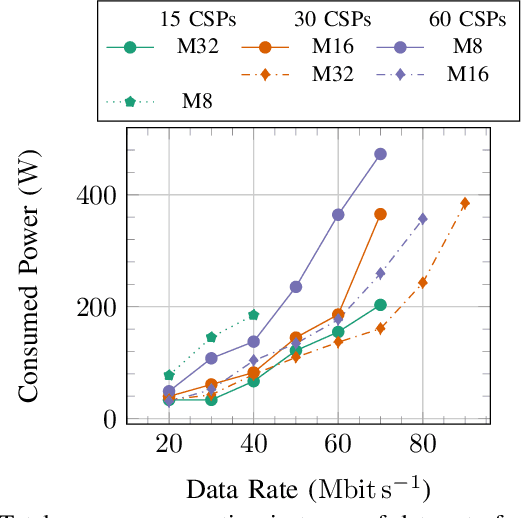
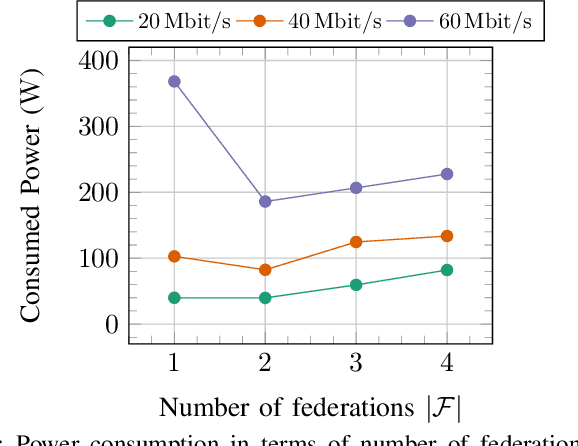
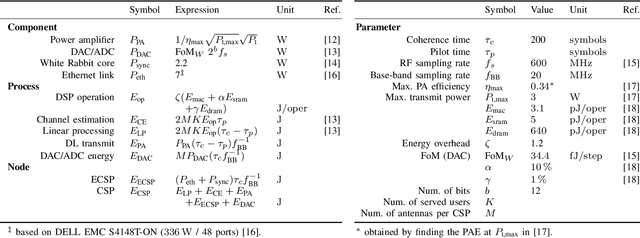
Energy Reduction in Cell-Free Massive MIMO through Fine-Grained Resource Management

The physical layer foundations of cell-free massive MIMO (CF-mMIMO) have been well-established. As a next step, researchers are investigating practical and energy-efficient network implementations. This paper focuses on multiple sets of access points (APs) where user equipments (UEs) are served in each set, termed a federation, without inter-federation interference. The combination of federations and CF-mMIMO shows promise for highly-loaded scenarios. Our aim is to minimize the total energy consumption while adhering to UE downlink data rate constraints. The energy expenditure of the full system is modelled using a detailed hardware model of the APs. We jointly design the AP-UE association variables, determine active APs, and assign APs and UEs to federations. To solve this highly combinatorial problem, we develop a novel alternating optimization algorithm. Simulation results for an indoor factory demonstrate the advantages of considering multiple federations, particularly when facing large data rate requirements. Furthermore, we show that adopting a more distributed CF-mMIMO architecture is necessary to meet the data rate requirements. Conversely, if feasible, using a less distributed system with more antennas at each AP is more advantageous from an energy savings perspective.

Enhancing Privacy in Federated Learning through Local Training

In this paper we propose the federated private local training algorithm (Fed-PLT) for federated learning, to overcome the challenges of (i) expensive communications and (ii) privacy preservation. We address (i) by allowing for both partial participation and local training, which significantly reduce the number of communication rounds between the central coordinator and computing agents. The algorithm matches the state of the art in the sense that the use of local training demonstrably does not impact accuracy. Additionally, agents have the flexibility to choose from various local training solvers, such as (stochastic) gradient descent and accelerated gradient descent. Further, we investigate how employing local training can enhance privacy, addressing point (ii). In particular, we derive differential privacy bounds and highlight their dependence on the number of local training epochs. We assess the effectiveness of the proposed algorithm by comparing it to alternative techniques, considering both theoretical analysis and numerical results from a classification task.

Online Distributed Learning over Random Networks

The recent deployment of multi-agent systems in a wide range of scenarios has enabled the solution of learning problems in a distributed fashion. In this context, agents are tasked with collecting local data and then cooperatively train a model, without directly sharing the data. While distributed learning offers the advantage of preserving agents' privacy, it also poses several challenges in terms of designing and analyzing suitable algorithms. This work focuses specifically on the following challenges motivated by practical implementation: (i) online learning, where the local data change over time; (ii) asynchronous agent computations; (iii) unreliable and limited communications; and (iv) inexact local computations. To tackle these challenges, we introduce the Distributed Operator Theoretical (DOT) version of the Alternating Direction Method of Multipliers (ADMM), which we call the DOT-ADMM Algorithm. We prove that it converges with a linear rate for a large class of convex learning problems (e.g., linear and logistic regression problems) toward a bounded neighborhood of the optimal time-varying solution, and characterize how the neighborhood depends on~$\text{(i)--(iv)}$. We corroborate the theoretical analysis with numerical simulations comparing the DOT-ADMM Algorithm with other state-of-the-art algorithms, showing that only the proposed algorithm exhibits robustness to (i)--(iv).

Online Distributed Learning with Quantized Finite-Time Coordination

In this paper we consider online distributed learning problems. Online distributed learning refers to the process of training learning models on distributed data sources. In our setting a set of agents need to cooperatively train a learning model from streaming data. Differently from federated learning, the proposed approach does not rely on a central server but only on peer-to-peer communications among the agents. This approach is often used in scenarios where data cannot be moved to a centralized location due to privacy, security, or cost reasons. In order to overcome the absence of a central server, we propose a distributed algorithm that relies on a quantized, finite-time coordination protocol to aggregate the locally trained models. Furthermore, our algorithm allows for the use of stochastic gradients during local training. Stochastic gradients are computed using a randomly sampled subset of the local training data, which makes the proposed algorithm more efficient and scalable than traditional gradient descent. In our paper, we analyze the performance of the proposed algorithm in terms of the mean distance from the online solution. Finally, we present numerical results for a logistic regression task.