Source-Guided Flow Matching

Guidance of generative models is typically achieved by modifying the probability flow vector field through the addition of a guidance field. In this paper, we instead propose the Source-Guided Flow Matching (SGFM) framework, which modifies the source distribution directly while keeping the pre-trained vector field intact. This reduces the guidance problem to a well-defined problem of sampling from the source distribution. We theoretically show that SGFM recovers the desired target distribution exactly. Furthermore, we provide bounds on the Wasserstein error for the generated distribution when using an approximate sampler of the source distribution and an approximate vector field. The key benefit of our approach is that it allows the user to flexibly choose the sampling method depending on their specific problem. To illustrate this, we systematically compare different sampling methods and discuss conditions for asymptotically exact guidance. Moreover, our framework integrates well with optimal flow matching models since the straight transport map generated by the vector field is preserved. Experimental results on synthetic 2D benchmarks, image datasets, and physics-informed generative tasks demonstrate the effectiveness and flexibility of the proposed framework.

Closed-Loop Neural Operator-Based Observer of Traffic Density

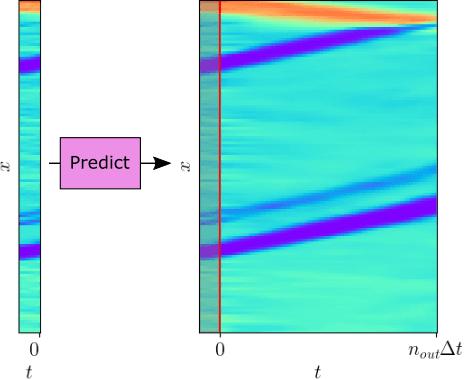
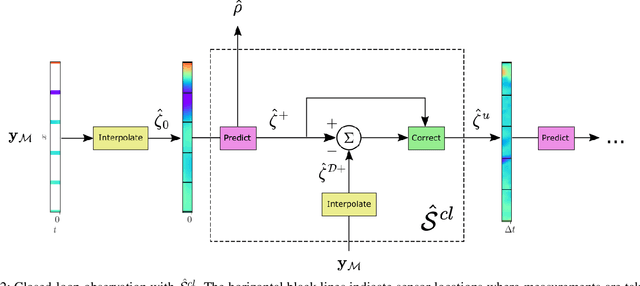
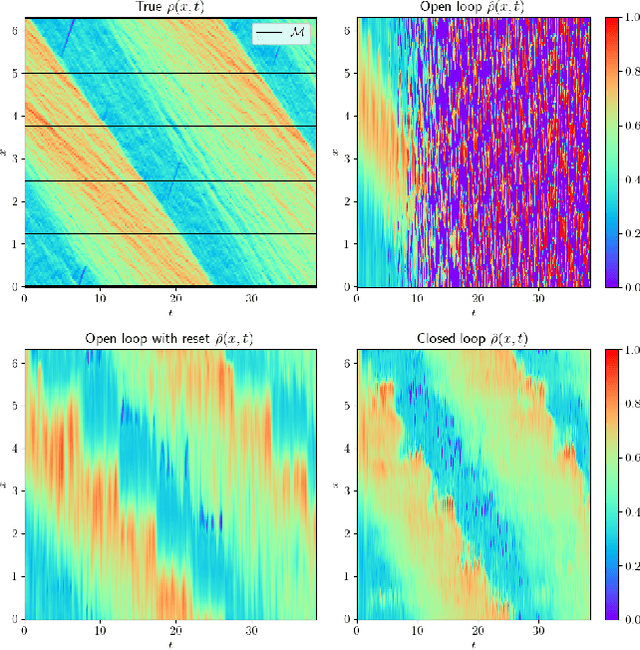
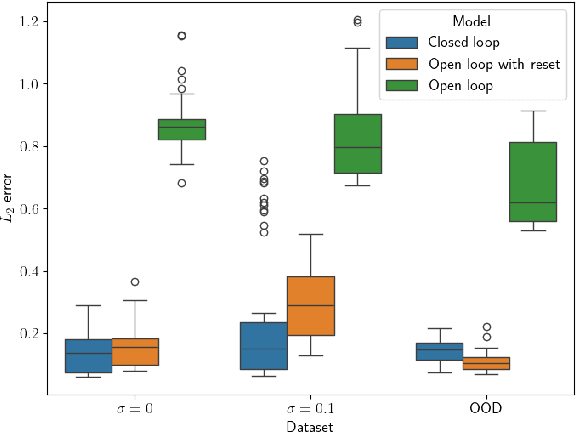
We consider the problem of traffic density estimation with sparse measurements from stationary roadside sensors. Our approach uses Fourier neural operators to learn macroscopic traffic flow dynamics from high-fidelity microscopic-level simulations. During inference, the operator functions as an open-loop predictor of traffic evolution. To close the loop, we couple the open-loop operator with a correction operator that combines the predicted density with sparse measurements from the sensors. Simulations with the SUMO software indicate that, compared to open-loop observers, the proposed closed-loop observer exhibit classical closed-loop properties such as robustness to noise and ultimate boundedness of the error. This shows the advantages of combining learned physics with real-time corrections, and opens avenues for accurate, efficient, and interpretable data-driven observers.

Online Traffic Density Estimation using Physics-Informed Neural Networks

Recent works on the application of Physics-Informed Neural Networks to traffic density estimation have shown to be promising for future developments due to their robustness to model errors and noisy data. In this paper, we introduce a methodology for online approximation of the traffic density using measurements from probe vehicles in two settings: one using the Greenshield model and the other considering a high-fidelity traffic simulation. The proposed method continuously estimates the real-time traffic density in space and performs model identification with each new set of measurements. The density estimate is updated in almost real-time using gradient descent and adaptive weights. In the case of full model knowledge, the resulting algorithm has similar performance to the classical open-loop one. However, in the case of model mismatch, the iterative solution behaves as a closed-loop observer and outperforms the baseline method. Similarly, in the high-fidelity setting, the proposed algorithm correctly reproduces the traffic characteristics.

Accuracy and Robustness of Weight-Balancing Methods for Training PINNs

Physics-Informed Neural Networks (PINNs) have emerged as powerful tools for integrating physics-based models with data by minimizing both data and physics losses. However, this multi-objective optimization problem is notoriously challenging, with some benchmark problems leading to unfeasible solutions. To address these issues, various strategies have been proposed, including adaptive weight adjustments in the loss function. In this work, we introduce clear definitions of accuracy and robustness in the context of PINNs and propose a novel training algorithm based on the Primal-Dual (PD) optimization framework. Our approach enhances the robustness of PINNs while maintaining comparable performance to existing weight-balancing methods. Numerical experiments demonstrate that the PD method consistently achieves reliable solutions across all investigated cases and can be easily implemented, facilitating its practical adoption. The code is available at https://github.com/haoming-SHEN/Accuracy-and-Robustness-of-Weight-Balancing-Methods-for-Training-PINNs.git.

Data-Driven vs Traditional Approaches to Power Transformer's Top-Oil Temperature Estimation

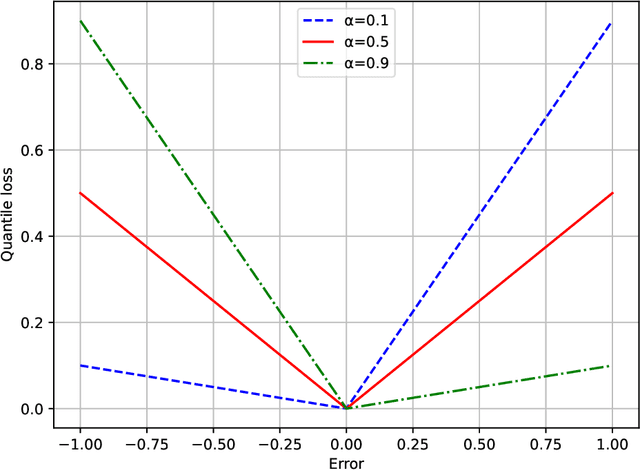
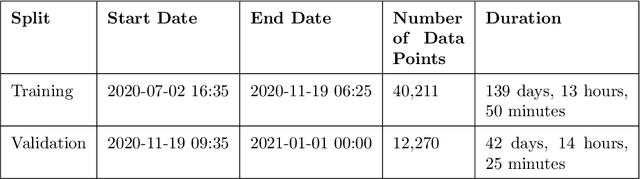
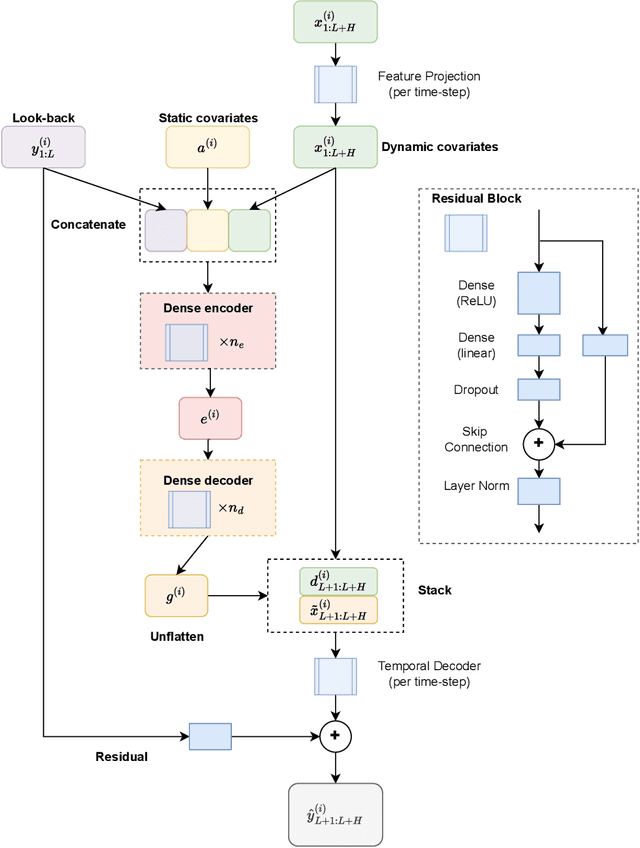
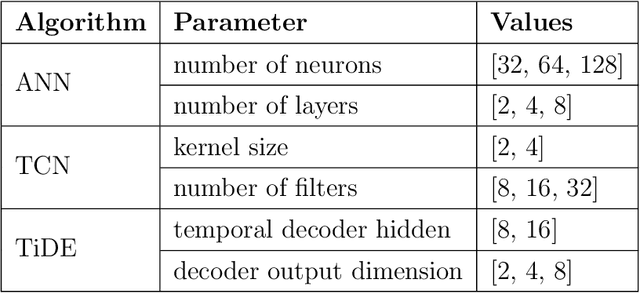
Power transformers are subjected to electrical currents and temperature fluctuations that, if not properly controlled, can lead to major deterioration of their insulation system. Therefore, monitoring the temperature of a power transformer is fundamental to ensure a long-term operational life. Models presented in the IEC 60076-7 and IEEE standards, for example, monitor the temperature by calculating the top-oil and the hot-spot temperatures. However, these models are not very accurate and rely on the power transformers' properties. This paper focuses on finding an alternative method to predict the top-oil temperatures given previous measurements. Given the large quantities of data available, machine learning methods for time series forecasting are analyzed and compared to the real measurements and the corresponding prediction of the IEC standard. The methods tested are Artificial Neural Networks (ANNs), Time-series Dense Encoder (TiDE), and Temporal Convolutional Networks (TCN) using different combinations of historical measurements. Each of these methods outperformed the IEC 60076-7 model and they are extended to estimate the temperature rise over ambient. To enhance prediction reliability, we explore the application of quantile regression to construct prediction intervals for the expected top-oil temperature ranges. The best-performing model successfully estimates conditional quantiles that provide sufficient coverage.

MILP initialization for solving parabolic PDEs with PINNs

Physics-Informed Neural Networks (PINNs) are a powerful deep learning method capable of providing solutions and parameter estimations of physical systems. Given the complexity of their neural network structure, the convergence speed is still limited compared to numerical methods, mainly when used in applications that model realistic systems. The network initialization follows a random distribution of the initial weights, as in the case of traditional neural networks, which could lead to severe model convergence bottlenecks. To overcome this problem, we follow current studies that deal with optimal initial weights in traditional neural networks. In this paper, we use a convex optimization model to improve the initialization of the weights in PINNs and accelerate convergence. We investigate two optimization models as a first training step, defined as pre-training, one involving only the boundaries and one including physics. The optimization is focused on the first layer of the neural network part of the PINN model, while the other weights are randomly initialized. We test the methods using a practical application of the heat diffusion equation to model the temperature distribution of power transformers. The PINN model with boundary pre-training is the fastest converging method at the current stage.

KKL Observer Synthesis for Nonlinear Systems via Physics-Informed Learning

This paper proposes a novel learning approach for designing Kazantzis-Kravaris/Luenberger (KKL) observers for autonomous nonlinear systems. The design of a KKL observer involves finding an injective map that transforms the system state into a higher-dimensional observer state, whose dynamics is linear and stable. The observer's state is then mapped back to the original system coordinates via the inverse map to obtain the state estimate. However, finding this transformation and its inverse is quite challenging. We propose to sequentially approximate these maps by neural networks that are trained using physics-informed learning. We generate synthetic data for training by numerically solving the system and observer dynamics. Theoretical guarantees for the robustness of state estimation against approximation error and system uncertainties are provided. Additionally, a systematic method for optimizing observer performance through parameter selection is presented. The effectiveness of the proposed approach is demonstrated through numerical simulations on benchmark examples and its application to sensor fault detection and isolation in a network of Kuramoto oscillators using learned KKL observers.

Learning and Verifying Maximal Taylor-Neural Lyapunov functions

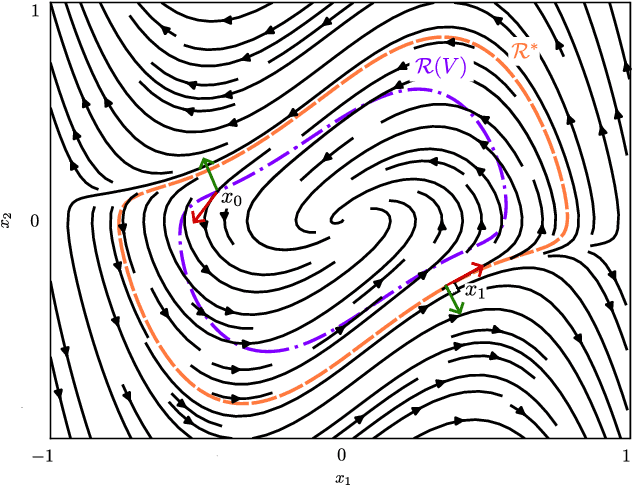
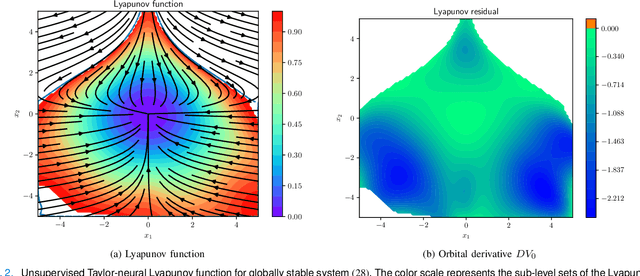
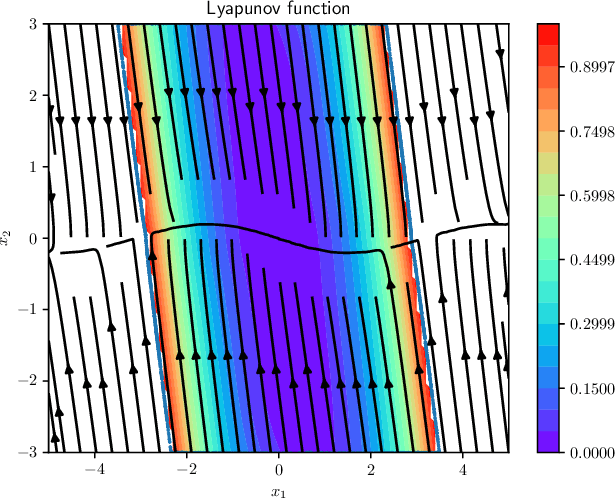
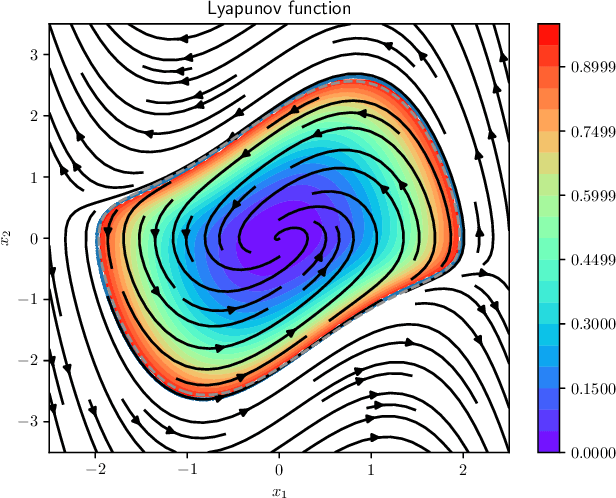
We introduce a novel neural network architecture, termed Taylor-neural Lyapunov functions, designed to approximate Lyapunov functions with formal certification. This architecture innovatively encodes local approximations and extends them globally by leveraging neural networks to approximate the residuals. Our method recasts the problem of estimating the largest region of attraction - specifically for maximal Lyapunov functions - into a learning problem, ensuring convergence around the origin through robust control theory. Physics-informed machine learning techniques further refine the estimation of the largest region of attraction. Remarkably, this method is versatile, operating effectively even without simulated data points. We validate the efficacy of our approach by providing numerical certificates of convergence across multiple examples. Our proposed methodology not only competes closely with state-of-the-art approaches, such as sum-of-squares and LyZNet, but also achieves comparable results even in the absence of simulated data. This work represents a significant advancement in control theory, with broad potential applications in the design of stable control systems and beyond.