Byzantine-Robust and Communication-Efficient Distributed Learning via Compressed Momentum Filtering

Distributed learning has become the standard approach for training large-scale machine learning models across private data silos. While distributed learning enhances privacy preservation and training efficiency, it faces critical challenges related to Byzantine robustness and communication reduction. Existing Byzantine-robust and communication-efficient methods rely on full gradient information either at every iteration or at certain iterations with a probability, and they only converge to an unnecessarily large neighborhood around the solution. Motivated by these issues, we propose a novel Byzantine-robust and communication-efficient stochastic distributed learning method that imposes no requirements on batch size and converges to a smaller neighborhood around the optimal solution than all existing methods, aligning with the theoretical lower bound. Our key innovation is leveraging Polyak Momentum to mitigate the noise caused by both biased compressors and stochastic gradients, thus defending against Byzantine workers under information compression. We provide proof of tight complexity bounds for our algorithm in the context of non-convex smooth loss functions, demonstrating that these bounds match the lower bounds in Byzantine-free scenarios. Finally, we validate the practical significance of our algorithm through an extensive series of experiments, benchmarking its performance on both binary classification and image classification tasks.

A survey on secure decentralized optimization and learning

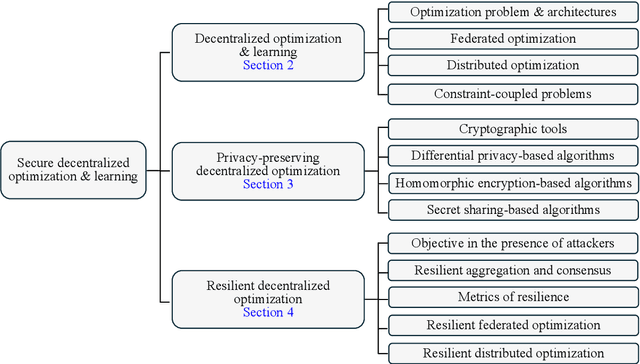
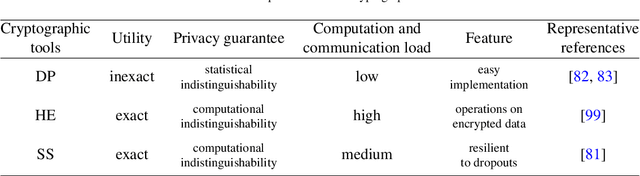
Decentralized optimization has become a standard paradigm for solving large-scale decision-making problems and training large machine learning models without centralizing data. However, this paradigm introduces new privacy and security risks, with malicious agents potentially able to infer private data or impair the model accuracy. Over the past decade, significant advancements have been made in developing secure decentralized optimization and learning frameworks and algorithms. This survey provides a comprehensive tutorial on these advancements. We begin with the fundamentals of decentralized optimization and learning, highlighting centralized aggregation and distributed consensus as key modules exposed to security risks in federated and distributed optimization, respectively. Next, we focus on privacy-preserving algorithms, detailing three cryptographic tools and their integration into decentralized optimization and learning systems. Additionally, we examine resilient algorithms, exploring the design and analysis of resilient aggregation and consensus protocols that support these systems. We conclude the survey by discussing current trends and potential future directions.

Federated Cubic Regularized Newton Learning with Sparsification-amplified Differential Privacy

This paper investigates the use of the cubic-regularized Newton method within a federated learning framework while addressing two major concerns that commonly arise in federated learning: privacy leakage and communication bottleneck. We introduce a federated learning algorithm called Differentially Private Federated Cubic Regularized Newton (DP-FCRN). By leveraging second-order techniques, our algorithm achieves lower iteration complexity compared to first-order methods. We also incorporate noise perturbation during local computations to ensure privacy. Furthermore, we employ sparsification in uplink transmission, which not only reduces the communication costs but also amplifies the privacy guarantee. Specifically, this approach reduces the necessary noise intensity without compromising privacy protection. We analyze the convergence properties of our algorithm and establish the privacy guarantee. Finally, we validate the effectiveness of the proposed algorithm through experiments on a benchmark dataset.

Enhancing Privacy in Federated Learning through Local Training

In this paper we propose the federated private local training algorithm (Fed-PLT) for federated learning, to overcome the challenges of (i) expensive communications and (ii) privacy preservation. We address (i) by allowing for both partial participation and local training, which significantly reduce the number of communication rounds between the central coordinator and computing agents. The algorithm matches the state of the art in the sense that the use of local training demonstrably does not impact accuracy. Additionally, agents have the flexibility to choose from various local training solvers, such as (stochastic) gradient descent and accelerated gradient descent. Further, we investigate how employing local training can enhance privacy, addressing point (ii). In particular, we derive differential privacy bounds and highlight their dependence on the number of local training epochs. We assess the effectiveness of the proposed algorithm by comparing it to alternative techniques, considering both theoretical analysis and numerical results from a classification task.

Near-Optimal Resilient Aggregation Rules for Distributed Learning Using 1-Center and 1-Mean Clustering with Outliers

Byzantine machine learning has garnered considerable attention in light of the unpredictable faults that can occur in large-scale distributed learning systems. The key to secure resilience against Byzantine machines in distributed learning is resilient aggregation mechanisms. Although abundant resilient aggregation rules have been proposed, they are designed in ad-hoc manners, imposing extra barriers on comparing, analyzing, and improving the rules across performance criteria. This paper studies near-optimal aggregation rules using clustering in the presence of outliers. Our outlier-robust clustering approach utilizes geometric properties of the update vectors provided by workers. Our analysis show that constant approximations to the 1-center and 1-mean clustering problems with outliers provide near-optimal resilient aggregators for metric-based criteria, which have been proven to be crucial in the homogeneous and heterogeneous cases respectively. In addition, we discuss two contradicting types of attacks under which no single aggregation rule is guaranteed to improve upon the naive average. Based on the discussion, we propose a two-phase resilient aggregation framework. We run experiments for image classification using a non-convex loss function. The proposed algorithms outperform previously known aggregation rules by a large margin with both homogeneous and heterogeneous data distributions among non-faulty workers. Code and appendix are available at https://github.com/jerry907/AAAI24-RASHB.

Asynchronous Distributed Optimization with Delay-free Parameters

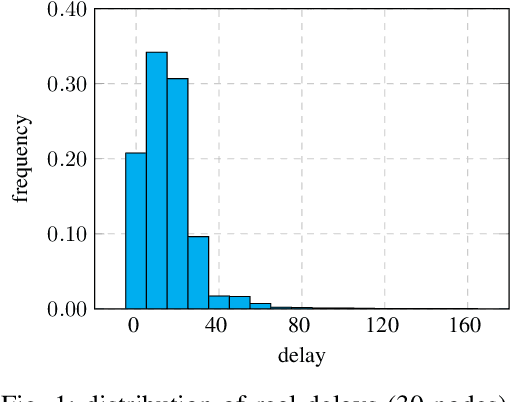
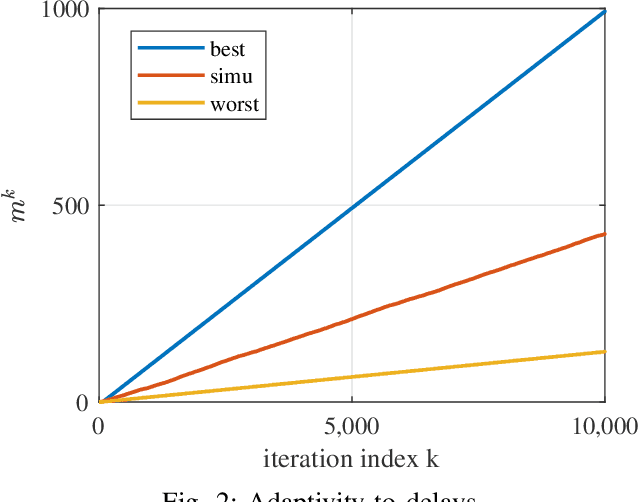
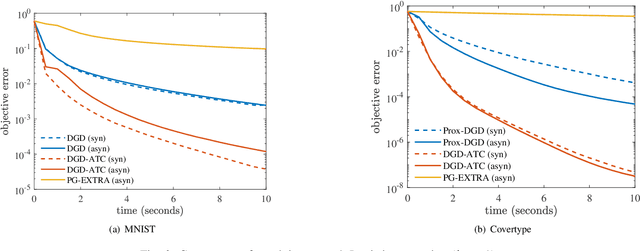
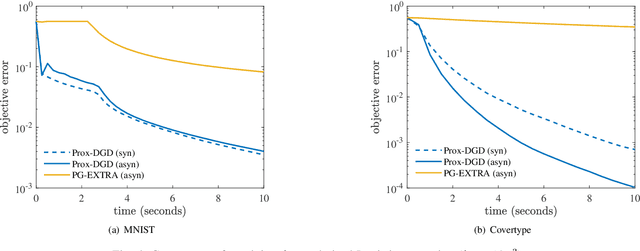
Existing asynchronous distributed optimization algorithms often use diminishing step-sizes that cause slow practical convergence, or use fixed step-sizes that depend on and decrease with an upper bound of the delays. Not only are such delay bounds hard to obtain in advance, but they also tend to be large and rarely attained, resulting in unnecessarily slow convergence. This paper develops asynchronous versions of two distributed algorithms, Prox-DGD and DGD-ATC, for solving consensus optimization problems over undirected networks. In contrast to alternatives, our algorithms can converge to the fixed point set of their synchronous counterparts using step-sizes that are independent of the delays. We establish convergence guarantees for strongly and weakly convex problems under both partial and total asynchrony. We also show that the convergence speed of the two asynchronous methods adapts to the actual level of asynchrony rather than being constrained by the worst-case. Numerical experiments demonstrate a strong practical performance of our asynchronous algorithms.

Achieving Model Fairness in Vertical Federated Learning

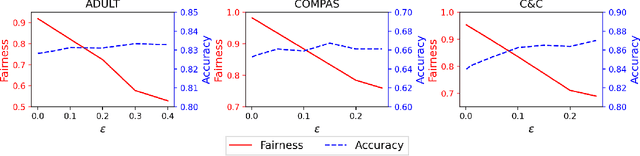
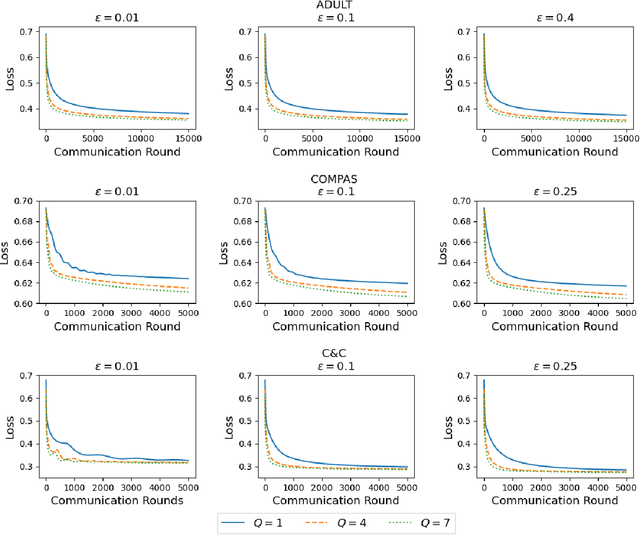
Vertical federated learning (VFL), which enables multiple enterprises possessing non-overlapped features to strengthen their machine learning models without disclosing their private data and model parameters, has received increasing attention lately. Similar to other machine learning algorithms, VFL suffers from fairness issues, i.e., the learned model may be unfairly discriminatory over the group with sensitive attributes. To tackle this problem, we propose a fair VFL framework in this work. First, we systematically formulate the problem of training fair models in VFL, where the learning task is modeled as a constrained optimization problem. To solve it in a federated manner, we consider its equivalent dual form and develop an asynchronous gradient coordinate-descent ascent algorithm, where each data party performs multiple parallelized local updates per communication round to effectively reduce the number of communication rounds. We prove that the algorithm finds a $\delta$-stationary point of the dual objective in $\mathcal{O}(\delta^{-4})$ communication rounds under mild conditions. Finally, extensive experiments on three benchmark datasets demonstrate the superior performance of our method in training fair models.

Improving Fairness for Data Valuation in Federated Learning

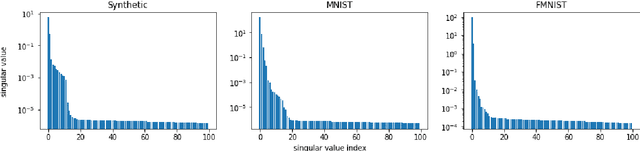
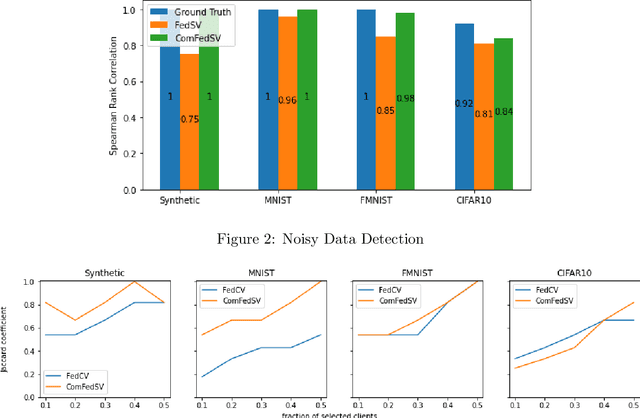
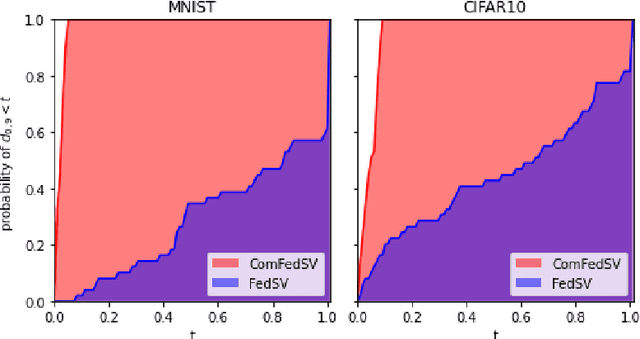
Federated learning is an emerging decentralized machine learning scheme that allows multiple data owners to work collaboratively while ensuring data privacy. The success of federated learning depends largely on the participation of data owners. To sustain and encourage data owners' participation, it is crucial to fairly evaluate the quality of the data provided by the data owners and reward them correspondingly. Federated Shapley value, recently proposed by Wang et al. [Federated Learning, 2020], is a measure for data value under the framework of federated learning that satisfies many desired properties for data valuation. However, there are still factors of potential unfairness in the design of federated Shapley value because two data owners with the same local data may not receive the same evaluation. We propose a new measure called completed federated Shapley value to improve the fairness of federated Shapley value. The design depends on completing a matrix consisting of all the possible contributions by different subsets of the data owners. It is shown under mild conditions that this matrix is approximately low-rank by leveraging concepts and tools from optimization. Both theoretical analysis and empirical evaluation verify that the proposed measure does improve fairness in many circumstances.