Michael P. Friedlander
STARK denoises spatial transcriptomics images via adaptive regularization
Dec 10, 2025Abstract:We present an approach to denoising spatial transcriptomics images that is particularly effective for uncovering cell identities in the regime of ultra-low sequencing depths, and also allows for interpolation of gene expression. The method -- Spatial Transcriptomics via Adaptive Regularization and Kernels (STARK) -- augments kernel ridge regression with an incrementally adaptive graph Laplacian regularizer. In each iteration, we (1) perform kernel ridge regression with a fixed graph to update the image, and (2) update the graph based on the new image. The kernel ridge regression step involves reducing the infinite dimensional problem on a space of images to finite dimensions via a modified representer theorem. Starting with a purely spatial graph, and updating it as we improve our image makes the graph more robust to noise in low sequencing depth regimes. We show that the aforementioned approach optimizes a block-convex objective through an alternating minimization scheme wherein the sub-problems have closed form expressions that are easily computed. This perspective allows us to prove convergence of the iterates to a stationary point of this non-convex objective. Statistically, such stationary points converge to the ground truth with rate $\mathcal{O}(R^{-1/2})$ where $R$ is the number of reads. In numerical experiments on real spatial transcriptomics data, the denoising performance of STARK, evaluated in terms of label transfer accuracy, shows consistent improvement over the competing methods tested.
Decentralized Optimization with Topology-Independent Communication
Sep 17, 2025Abstract:Distributed optimization requires nodes to coordinate, yet full synchronization scales poorly. When $n$ nodes collaborate through $m$ pairwise regularizers, standard methods demand $\mathcal{O}(m)$ communications per iteration. This paper proposes randomized local coordination: each node independently samples one regularizer uniformly and coordinates only with nodes sharing that term. This exploits partial separability, where each regularizer $G_j$ depends on a subset $S_j \subseteq \{1,\ldots,n\}$ of nodes. For graph-guided regularizers where $|S_j|=2$, expected communication drops to exactly 2 messages per iteration. This method achieves $\tilde{\mathcal{O}}(\varepsilon^{-2})$ iterations for convex objectives and under strong convexity, $\mathcal{O}(\varepsilon^{-1})$ to an $\varepsilon$-solution and $\mathcal{O}(\log(1/\varepsilon))$ to a neighborhood. Replacing the proximal map of the sum $\sum_j G_j$ with the proximal map of a single randomly selected regularizer $G_j$ preserves convergence while eliminating global coordination. Experiments validate both convergence rates and communication efficiency across synthetic and real-world datasets.
Knowledge-Injected Federated Learning
Aug 16, 2022

Abstract:Federated learning is an emerging technique for training models from decentralized data sets. In many applications, data owners participating in the federated learning system hold not only the data but also a set of domain knowledge. Such knowledge includes human know-how and craftsmanship that can be extremely helpful to the federated learning task. In this work, we propose a federated learning framework that allows the injection of participants' domain knowledge, where the key idea is to refine the global model with knowledge locally. The scenario we consider is motivated by a real industry-level application, and we demonstrate the effectiveness of our approach to this application.
A dual approach for federated learning
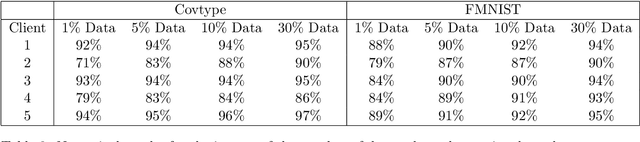
Feb 04, 2022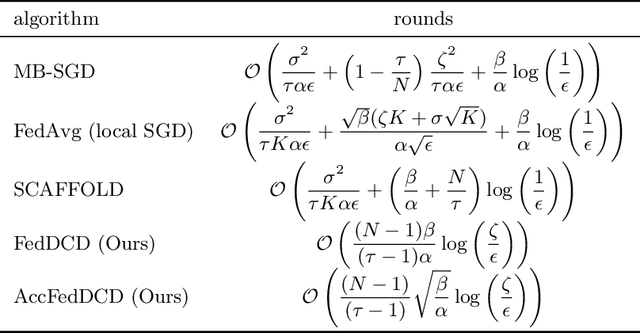
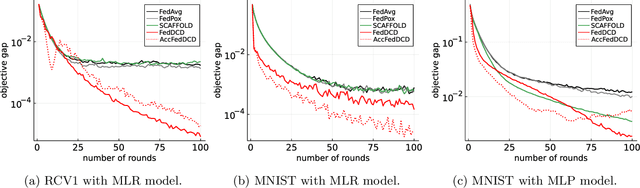
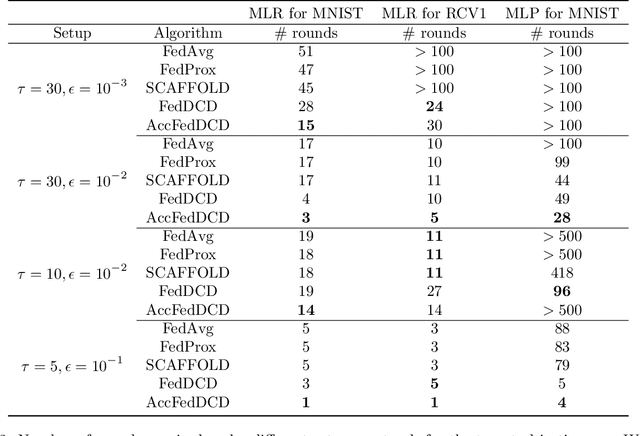
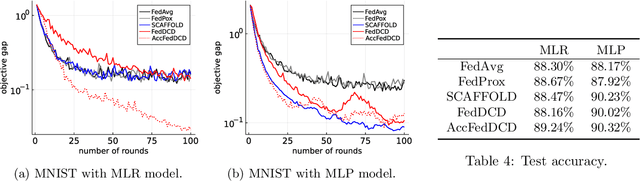
Abstract:We study the federated optimization problem from a dual perspective and propose a new algorithm termed federated dual coordinate descent (FedDCD), which is based on a type of coordinate descent method developed by Necora et al.[Journal of Optimization Theory and Applications, 2017]. Additionally, we enhance the FedDCD method with inexact gradient oracles and Nesterov's acceleration. We demonstrate theoretically that our proposed approach achieves better convergence rates than the state-of-the-art primal federated optimization algorithms under certain situations. Numerical experiments on real-world datasets support our analysis.
Fair and efficient contribution valuation for vertical federated learning
Jan 07, 2022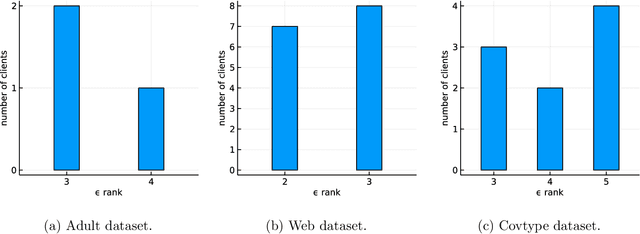
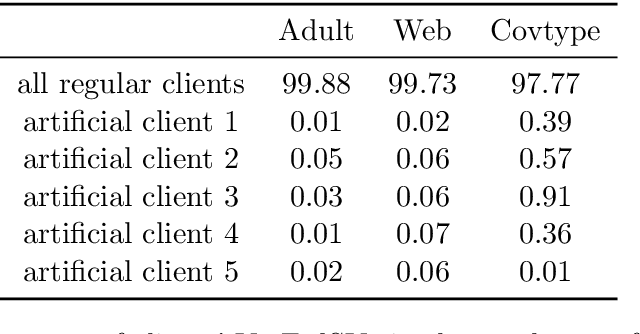
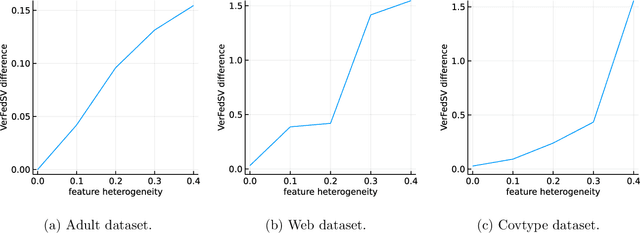
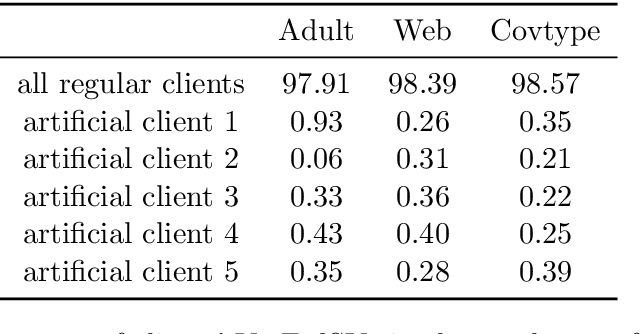
Abstract:Federated learning is a popular technology for training machine learning models on distributed data sources without sharing data. Vertical federated learning or feature-based federated learning applies to the cases that different data sources share the same sample ID space but differ in feature space. To ensure the data owners' long-term engagement, it is critical to objectively assess the contribution from each data source and recompense them accordingly. The Shapley value (SV) is a provably fair contribution valuation metric originated from cooperative game theory. However, computing the SV requires extensively retraining the model on each subset of data sources, which causes prohibitively high communication costs in federated learning. We propose a contribution valuation metric called vertical federated Shapley value (VerFedSV) based on SV. We show that VerFedSV not only satisfies many desirable properties for fairness but is also efficient to compute, and can be adapted to both synchronous and asynchronous vertical federated learning algorithms. Both theoretical analysis and extensive experimental results verify the fairness, efficiency, and adaptability of VerFedSV.
Improving Fairness for Data Valuation in Federated Learning
Sep 19, 2021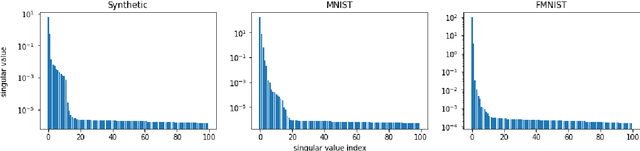
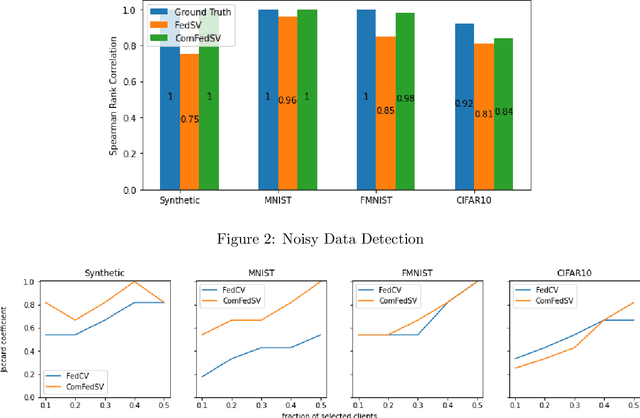
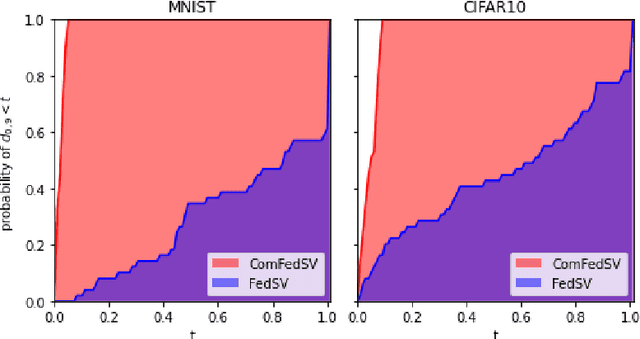
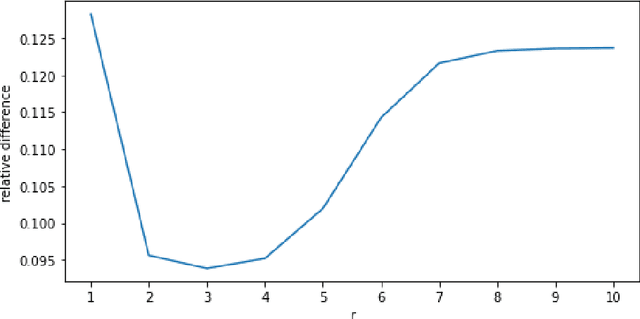
Abstract:Federated learning is an emerging decentralized machine learning scheme that allows multiple data owners to work collaboratively while ensuring data privacy. The success of federated learning depends largely on the participation of data owners. To sustain and encourage data owners' participation, it is crucial to fairly evaluate the quality of the data provided by the data owners and reward them correspondingly. Federated Shapley value, recently proposed by Wang et al. [Federated Learning, 2020], is a measure for data value under the framework of federated learning that satisfies many desired properties for data valuation. However, there are still factors of potential unfairness in the design of federated Shapley value because two data owners with the same local data may not receive the same evaluation. We propose a new measure called completed federated Shapley value to improve the fairness of federated Shapley value. The design depends on completing a matrix consisting of all the possible contributions by different subsets of the data owners. It is shown under mild conditions that this matrix is approximately low-rank by leveraging concepts and tools from optimization. Both theoretical analysis and empirical evaluation verify that the proposed measure does improve fairness in many circumstances.
Online mirror descent and dual averaging: keeping pace in the dynamic case
Jun 03, 2020
Abstract:Online mirror descent (OMD) and dual averaging (DA) are two fundamental algorithms for online convex optimization. They are known to have very similar (or even identical) performance guarantees in most scenarios when a \emph{fixed} learning rate is used. However, for \emph{dynamic} learning rates OMD is provably inferior to DA. It is known that, with a dynamic learning rate, OMD can suffer linear regret, even in common settings such as prediction with expert advice. This hints that the relationship between OMD and DA is not fully understood at present. In this paper, we modify the OMD algorithm by a simple technique that we call stabilization. We give essentially the same abstract regret bound for stabilized OMD and DA by modifying the classical OMD convergence analysis in a careful and modular way, yielding proofs that we believe to be clean and flexible. Simple corollaries of these bounds show that OMD with stabilization and DA enjoy the same performance guarantees in many applications even under dynamic learning rates. We also shed some light on the similarities between OMD and DA and show simple conditions under which stabilized OMD and DA generate the same iterates.
Smooth Structured Prediction Using Quantum and Classical Gibbs Samplers
Oct 01, 2018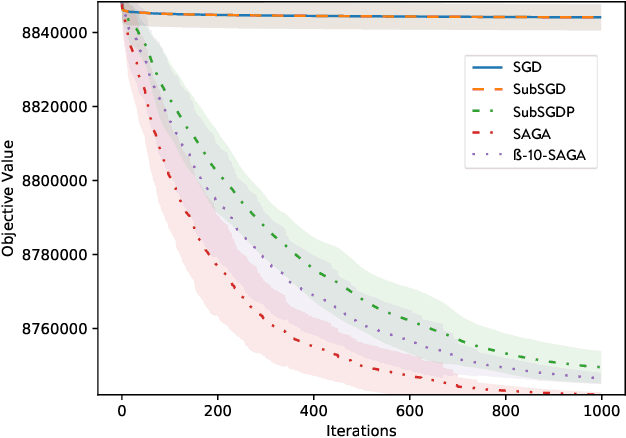
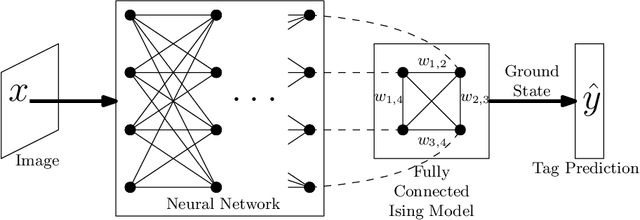


Abstract:We introduce a quantum algorithm for solving structured prediction problems with a runtime that scales with the square root of the size of the label space, but scales in $\widetilde O\left(\epsilon^{-2.5}\right)$ with respect to the precision of the solution. In doing so, we analyze a stochastic gradient algorithm for convex optimization in the presence of an additive error in the calculation of the gradients, and show that its convergence rate does not deteriorate if the additive errors are of the order $O(\sqrt\epsilon)$. Our algorithm uses quantum Gibbs sampling at temperature $O (\epsilon)$ as a subroutine. Numerical results using Monte Carlo simulations on an image tagging task demonstrate the benefit of the approach.
Fast Dual Variational Inference for Non-Conjugate LGMs
Jun 05, 2013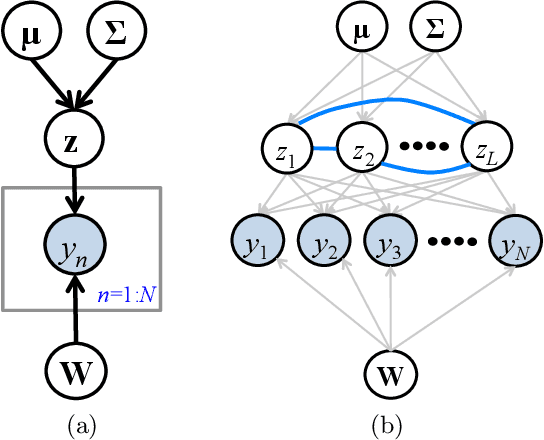
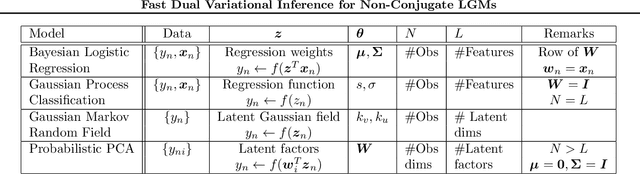

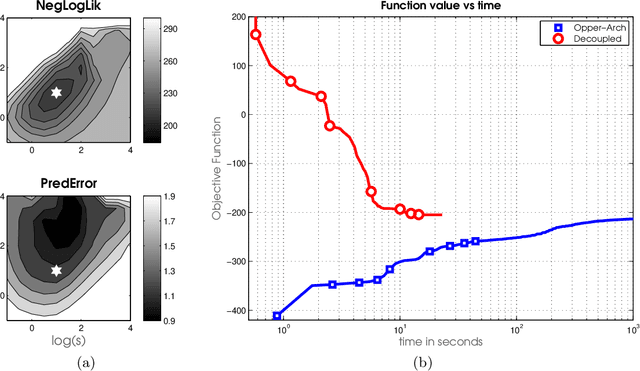
Abstract:Latent Gaussian models (LGMs) are widely used in statistics and machine learning. Bayesian inference in non-conjugate LGMs is difficult due to intractable integrals involving the Gaussian prior and non-conjugate likelihoods. Algorithms based on variational Gaussian (VG) approximations are widely employed since they strike a favorable balance between accuracy, generality, speed, and ease of use. However, the structure of the optimization problems associated with these approximations remains poorly understood, and standard solvers take too long to converge. We derive a novel dual variational inference approach that exploits the convexity property of the VG approximations. We obtain an algorithm that solves a convex optimization problem, reduces the number of variational parameters, and converges much faster than previous methods. Using real-world data, we demonstrate these advantages on a variety of LGMs, including Gaussian process classification, and latent Gaussian Markov random fields.
Hybrid Deterministic-Stochastic Methods for Data Fitting
Feb 09, 2013
Abstract:Many structured data-fitting applications require the solution of an optimization problem involving a sum over a potentially large number of measurements. Incremental gradient algorithms offer inexpensive iterations by sampling a subset of the terms in the sum. These methods can make great progress initially, but often slow as they approach a solution. In contrast, full-gradient methods achieve steady convergence at the expense of evaluating the full objective and gradient on each iteration. We explore hybrid methods that exhibit the benefits of both approaches. Rate-of-convergence analysis shows that by controlling the sample size in an incremental gradient algorithm, it is possible to maintain the steady convergence rates of full-gradient methods. We detail a practical quasi-Newton implementation based on this approach. Numerical experiments illustrate its potential benefits.
* 26 pages. Revised proofs of Theorems 2.6 and 3.1, results unchanged
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge