Smooth Structured Prediction Using Quantum and Classical Gibbs Samplers
Paper and Code
Oct 01, 2018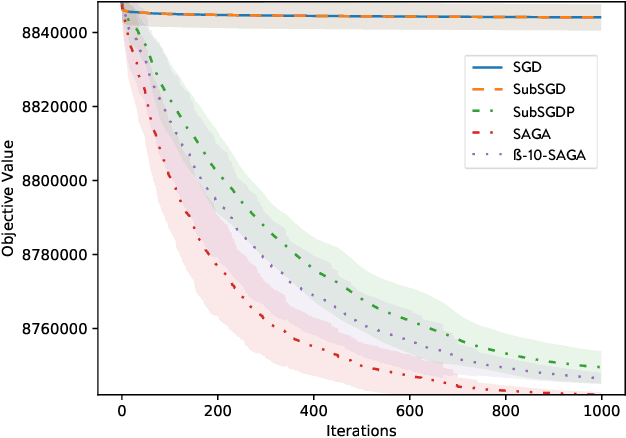
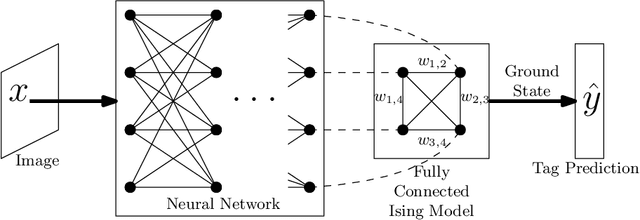


We introduce a quantum algorithm for solving structured prediction problems with a runtime that scales with the square root of the size of the label space, but scales in $\widetilde O\left(\epsilon^{-2.5}\right)$ with respect to the precision of the solution. In doing so, we analyze a stochastic gradient algorithm for convex optimization in the presence of an additive error in the calculation of the gradients, and show that its convergence rate does not deteriorate if the additive errors are of the order $O(\sqrt\epsilon)$. Our algorithm uses quantum Gibbs sampling at temperature $O (\epsilon)$ as a subroutine. Numerical results using Monte Carlo simulations on an image tagging task demonstrate the benefit of the approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge