A Cryogenic Memristive Neural Decoder for Fault-tolerant Quantum Error Correction

Neural decoders for quantum error correction (QEC) rely on neural networks to classify syndromes extracted from error correction codes and find appropriate recovery operators to protect logical information against errors. Despite the good performance of neural decoders, important practical requirements remain to be achieved, such as minimizing the decoding time to meet typical rates of syndrome generation in repeated error correction schemes, and ensuring the scalability of the decoding approach as the code distance increases. Designing a dedicated integrated circuit to perform the decoding task in co-integration with a quantum processor appears necessary to reach these decoding time and scalability requirements, as routing signals in and out of a cryogenic environment to be processed externally leads to unnecessary delays and an eventual wiring bottleneck. In this work, we report the design and performance analysis of a neural decoder inference accelerator based on an in-memory computing (IMC) architecture, where crossbar arrays of resistive memory devices are employed to both store the synaptic weights of the decoder neural network and perform analog matrix-vector multiplications during inference. In proof-of-concept numerical experiments supported by experimental measurements, we investigate the impact of TiO$_\textrm{x}$-based memristive devices' non-idealities on decoding accuracy. Hardware-aware training methods are developed to mitigate the loss in accuracy, allowing the memristive neural decoders to achieve a pseudo-threshold of $9.23\times 10^{-4}$ for the distance-three surface code, whereas the equivalent digital neural decoder achieves a pseudo-threshold of $1.01\times 10^{-3}$. This work provides a pathway to scalable, fast, and low-power cryogenic IMC hardware for integrated QEC.

On the Computational Cost of Stochastic Security

We investigate whether long-run persistent chain Monte Carlo simulation of Langevin dynamics improves the quality of the representations achieved by energy-based models (EBM). We consider a scheme wherein Monte Carlo simulation of a diffusion process using a trained EBM is used to improve the adversarial robustness and the calibration score of an independent classifier network. Our results show that increasing the computational budget of Gibbs sampling in persistent contrastive divergence improves the calibration and adversarial robustness of the model, elucidating the practical merit of realizing new quantum and classical hardware and software for efficient Gibbs sampling from continuous energy potentials.

Neural Error Mitigation of Near-Term Quantum Simulations

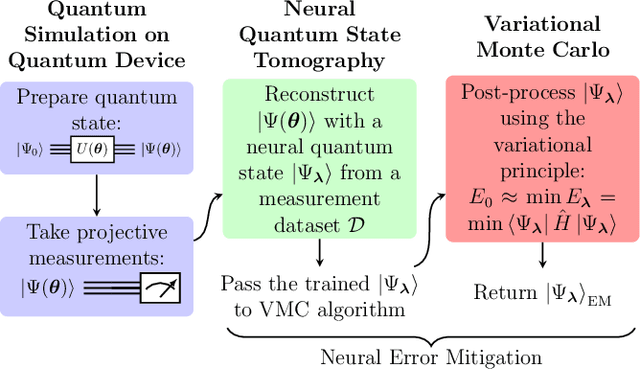
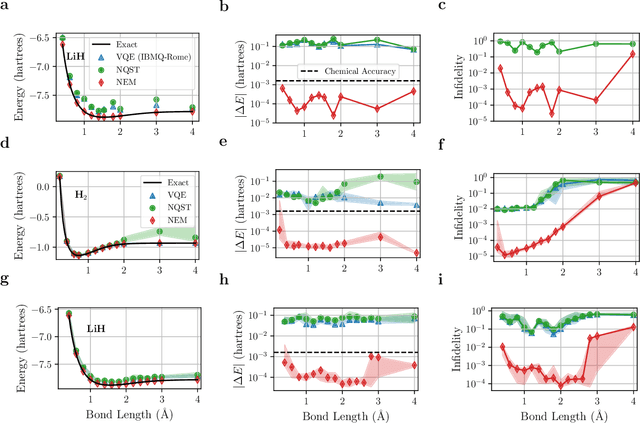
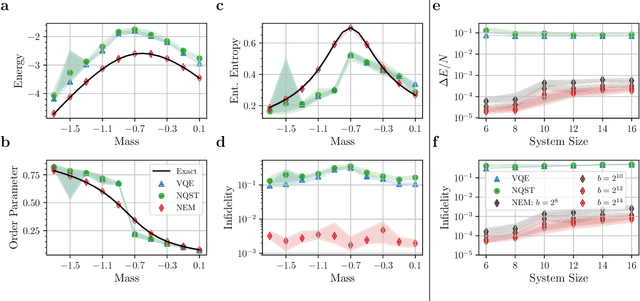
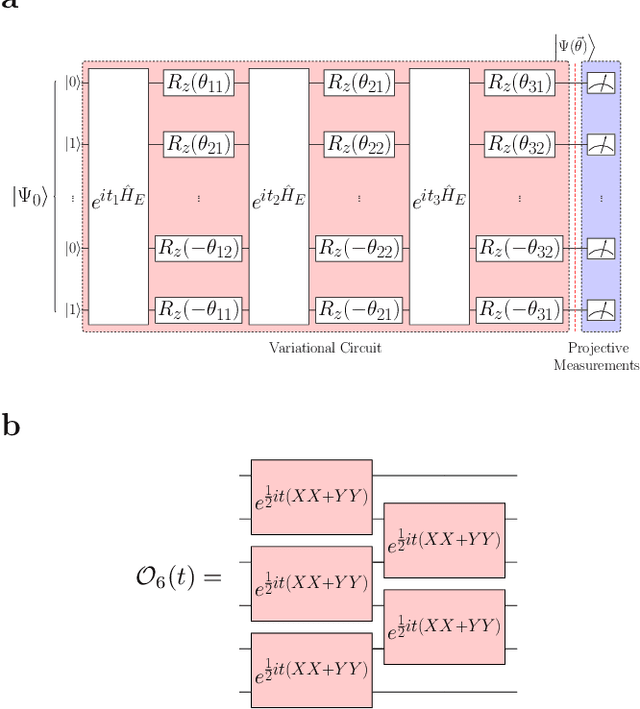
One of the promising applications of early quantum computers is the simulation of quantum systems. Variational methods for near-term quantum computers, such as the variational quantum eigensolver (VQE), are a promising approach to finding ground states of quantum systems relevant in physics, chemistry, and materials science. These approaches, however, are constrained by the effects of noise as well as the limited quantum resources of near-term quantum hardware, motivating the need for quantum error mitigation techniques to reduce the effects of noise. Here we introduce $\textit{neural error mitigation}$, a novel method that uses neural networks to improve estimates of ground states and ground-state observables obtained using VQE on near-term quantum computers. To demonstrate our method's versatility, we apply neural error mitigation to finding the ground states of H$_2$ and LiH molecular Hamiltonians, as well as the lattice Schwinger model. Our results show that neural error mitigation improves the numerical and experimental VQE computation to yield low-energy errors, low infidelities, and accurate estimations of more-complex observables like order parameters and entanglement entropy, without requiring additional quantum resources. Additionally, neural error mitigation is agnostic to both the quantum hardware and the particular noise channel, making it a versatile tool for quantum simulation. Applying quantum many-body machine learning techniques to error mitigation, our method is a promising strategy for extending the reach of near-term quantum computers to solve complex quantum simulation problems.

Smooth Structured Prediction Using Quantum and Classical Gibbs Samplers

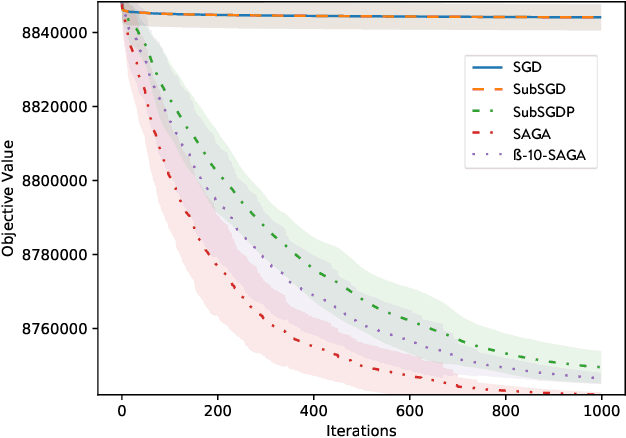
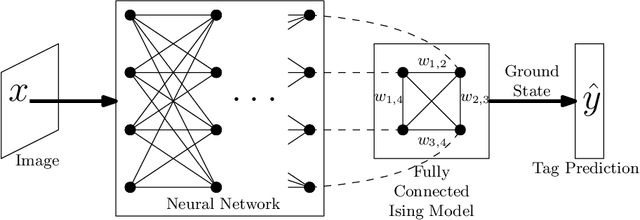
We introduce a quantum algorithm for solving structured prediction problems with a runtime that scales with the square root of the size of the label space, but scales in $\widetilde O\left(\epsilon^{-2.5}\right)$ with respect to the precision of the solution. In doing so, we analyze a stochastic gradient algorithm for convex optimization in the presence of an additive error in the calculation of the gradients, and show that its convergence rate does not deteriorate if the additive errors are of the order $O(\sqrt\epsilon)$. Our algorithm uses quantum Gibbs sampling at temperature $O (\epsilon)$ as a subroutine. Numerical results using Monte Carlo simulations on an image tagging task demonstrate the benefit of the approach.

Deep neural decoders for near term fault-tolerant experiments

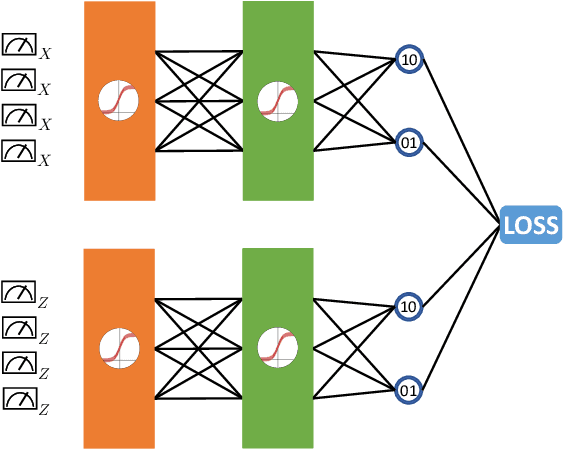
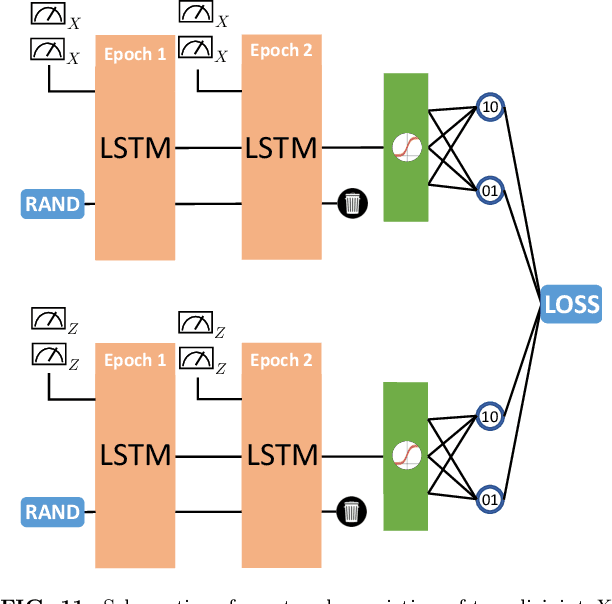
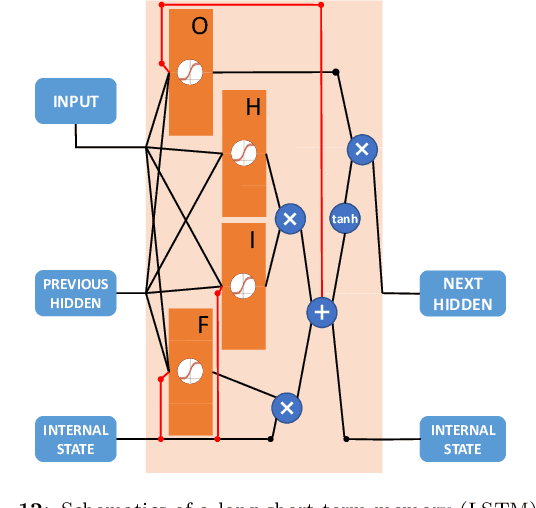
Finding efficient decoders for quantum error correcting codes adapted to realistic experimental noise in fault-tolerant devices represents a significant challenge. In this paper we introduce several decoding algorithms complemented by deep neural decoders and apply them to analyze several fault-tolerant error correction protocols such as the surface code as well as Steane and Knill error correction. Our methods require no knowledge of the underlying noise model afflicting the quantum device making them appealing for real-world experiments. Our analysis is based on a full circuit-level noise model. It considers both distance-three and five codes, and is performed near the codes pseudo-threshold regime. Training deep neural decoders in low noise rate regimes appears to be a challenging machine learning endeavour. We provide a detailed description of our neural network architectures and training methodology. We then discuss both the advantages and limitations of deep neural decoders. Lastly, we provide a rigorous analysis of the decoding runtime of trained deep neural decoders and compare our methods with anticipated gate times in future quantum devices. Given the broad applications of our decoding schemes, we believe that the methods presented in this paper could have practical applications for near term fault-tolerant experiments.

Free energy-based reinforcement learning using a quantum processor

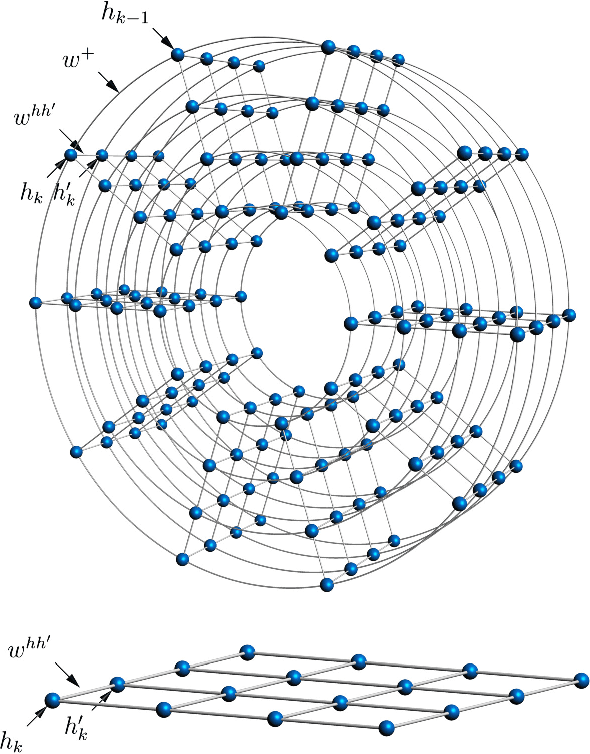
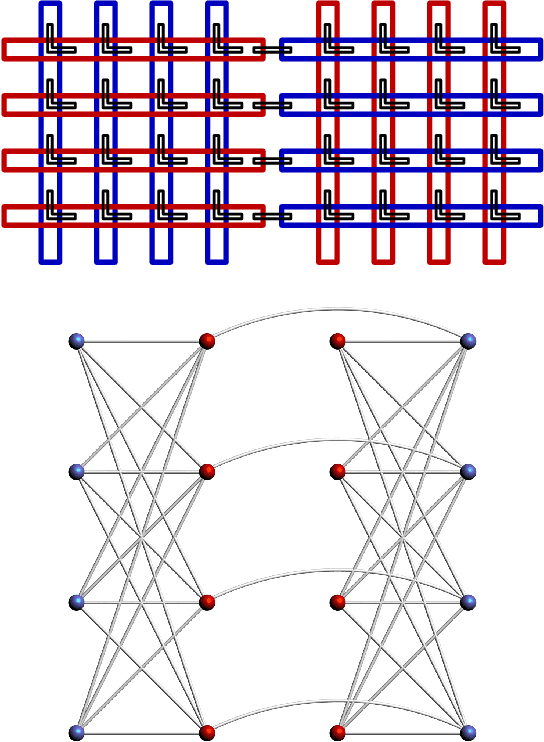
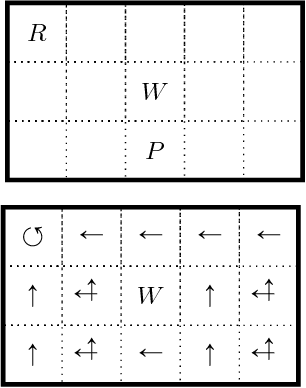
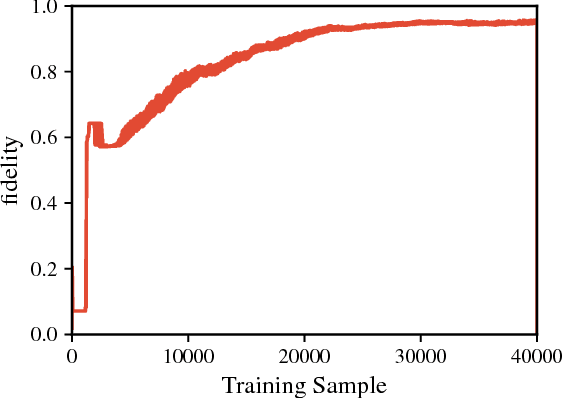
Recent theoretical and experimental results suggest the possibility of using current and near-future quantum hardware in challenging sampling tasks. In this paper, we introduce free energy-based reinforcement learning (FERL) as an application of quantum hardware. We propose a method for processing a quantum annealer's measured qubit spin configurations in approximating the free energy of a quantum Boltzmann machine (QBM). We then apply this method to perform reinforcement learning on the grid-world problem using the D-Wave 2000Q quantum annealer. The experimental results show that our technique is a promising method for harnessing the power of quantum sampling in reinforcement learning tasks.

Reinforcement Learning Using Quantum Boltzmann Machines

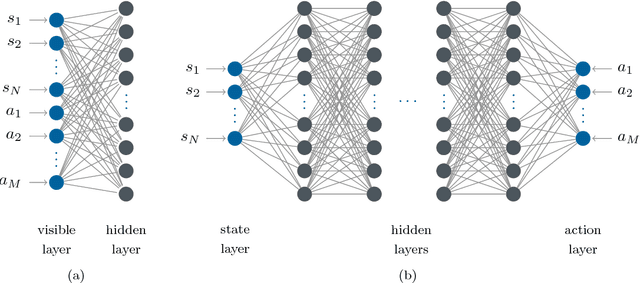
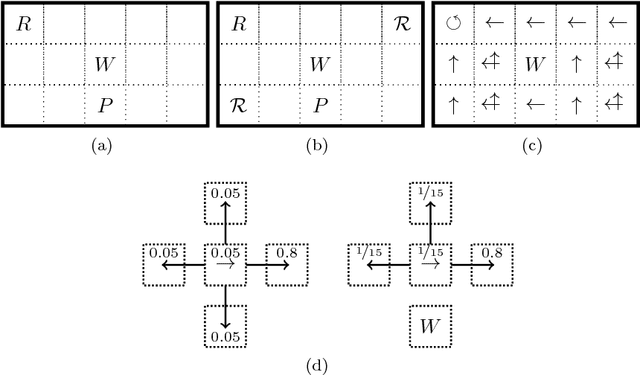
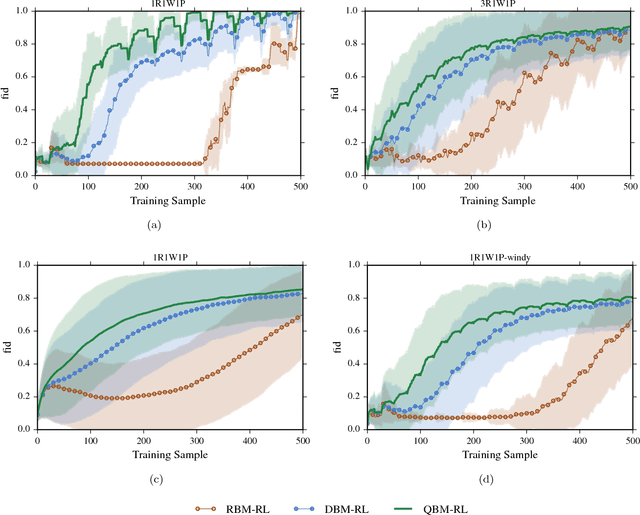
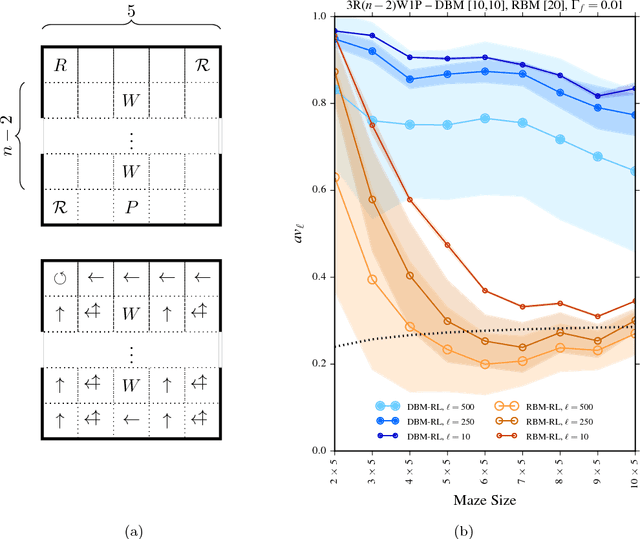
We investigate whether quantum annealers with select chip layouts can outperform classical computers in reinforcement learning tasks. We associate a transverse field Ising spin Hamiltonian with a layout of qubits similar to that of a deep Boltzmann machine (DBM) and use simulated quantum annealing (SQA) to numerically simulate quantum sampling from this system. We design a reinforcement learning algorithm in which the set of visible nodes representing the states and actions of an optimal policy are the first and last layers of the deep network. In absence of a transverse field, our simulations show that DBMs train more effectively than restricted Boltzmann machines (RBM) with the same number of weights. Since sampling from Boltzmann distributions of a DBM is not classically feasible, this is evidence of advantage of a non-Turing sampling oracle. We then develop a framework for training the network as a quantum Boltzmann machine (QBM) in the presence of a significant transverse field for reinforcement learning. This further improves the reinforcement learning method using DBMs.