Deep neural decoders for near term fault-tolerant experiments
Paper and Code
Apr 06, 2018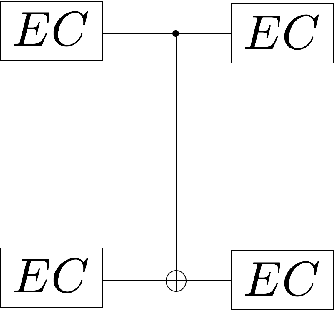
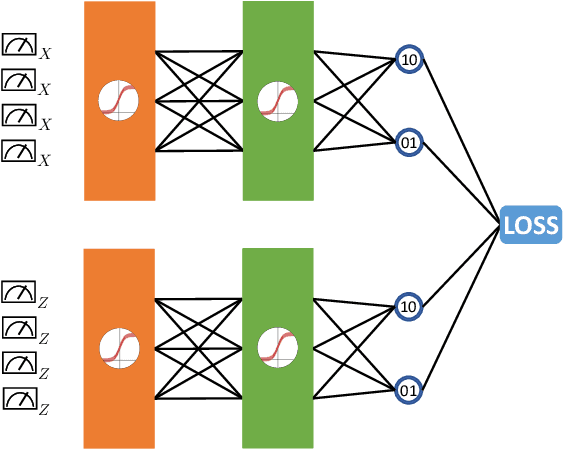
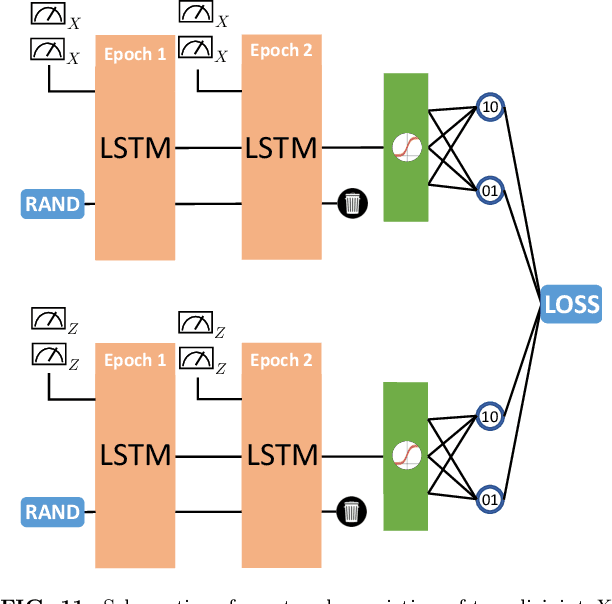
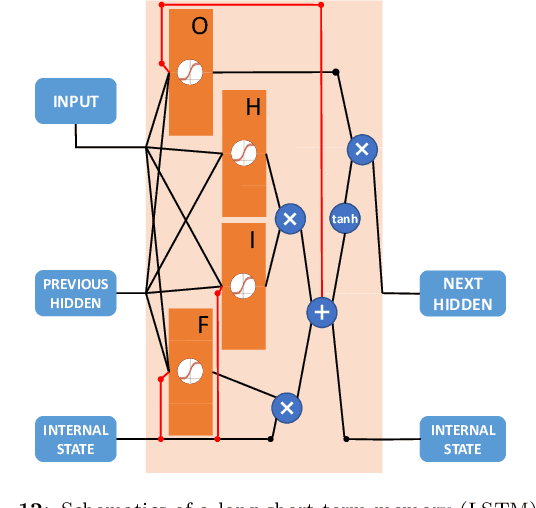
Finding efficient decoders for quantum error correcting codes adapted to realistic experimental noise in fault-tolerant devices represents a significant challenge. In this paper we introduce several decoding algorithms complemented by deep neural decoders and apply them to analyze several fault-tolerant error correction protocols such as the surface code as well as Steane and Knill error correction. Our methods require no knowledge of the underlying noise model afflicting the quantum device making them appealing for real-world experiments. Our analysis is based on a full circuit-level noise model. It considers both distance-three and five codes, and is performed near the codes pseudo-threshold regime. Training deep neural decoders in low noise rate regimes appears to be a challenging machine learning endeavour. We provide a detailed description of our neural network architectures and training methodology. We then discuss both the advantages and limitations of deep neural decoders. Lastly, we provide a rigorous analysis of the decoding runtime of trained deep neural decoders and compare our methods with anticipated gate times in future quantum devices. Given the broad applications of our decoding schemes, we believe that the methods presented in this paper could have practical applications for near term fault-tolerant experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge